江苏省淮安市淮安区2018-2019学年八年级下学期数学3月月考试试卷

试卷更新日期：2020-03-11 类型：月考试卷

进入出卷网下载

一、单选题

1. 以下问题，最适合用普查的是（）

A、了解我国初中学生视力状况的调查 B、对“3·15”晚会收视率的调查 C、对量子通信卫星上某种零部件的检查 D、对一批节能灯使用寿命的调查

查看试题解析
2. 下列成语描述的事件为随机事件的是（）

A、水涨船高 B、守株待兔 C、水中捞月 D、缘木求鱼

查看试题解析
3. 下列电视台的台标，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 下列说法错误的是（）

A、成中心对称的两个图形必能重合 B、两组对角分别相等的四边形是平行四边形 C、一组对边平行,一组对角相等的四边形是平行四边形 D、对角线相等的四边形是平行四边形

查看试题解析
5. 某校八年级共有500名学生,为了了解这些学生的视力情况,随机抽査了40名学生的视力,对所得数据进行整理.若数据在4.8～5.0这一小组的频率为0.4,则可估计该校八年级学生视力在4.8～5.0范围内的人数有（）

A、300 B、200 C、150 D、16

查看试题解析
6. 如图，在平行四边形 $A B C D$ 中， $∠ A B C$ 的平分线交 $A D$ 于 $E$ ， $A B = 4$ ， $B C = 6$ ，则 $D E$ 为（）

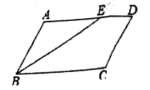A、10 B、5 C、3 D、2

查看试题解析
7. 以下说法合理的是：（）

A、“打开电视，正在播放新闻节日”是必然事件 B、“抛一枚硬币，正面朝上的概率为 $\frac{1}{2}$ ”表示每抛两次就有一次正面朝上 C、“抛掷一枚均匀的骰子，出现点数6的概率是 $\frac{1}{6}$ ”表示随着抛掷次数的增加“出现点数6”这一事件发生的频率稳定在 $\frac{1}{6}$ 附近 D、为了解某品牌火腿的质量，选择全面检测

查看试题解析
8. 如图，在 $R t Δ A B C$ 中， $∠ B A C = 90^{\circ}$ ，将 $Δ A B C$ 绕点 $A$ 顺时针旋转90°后得到 $Δ A B^{'} C^{'}$ （点 $B$ 的对应点是点 $B^{'}$ ，点 $C$ 的对应点是点 $C^{'}$ ），连接 $C C^{'}$ .若 $∠ C C^{'} B^{'} = 32^{\circ}$ ，则 $∠ B$ 的大小是（）

A、77° B、69° C、67° D、32°

查看试题解析

二、填空题

9. 荡秋千（填“属于”、“不属于”)旋转；

查看试题解析
10. 医生一般绘制统计图来反映病人的体温变化情况；

查看试题解析
11. 为了了解初二学生的体能情况，某校抽取了80名初二学生进行一分钟跳绳次数测试，将所得数据整理后，得到落在179.5至189.5的频率为0.35，则在179.5至189.5的频数是；

查看试题解析
12. 如图是某班40名同学的体重频数分布直方图，体重超过 $59.5 k g$ 的频率是；

查看试题解析
13. 在平行四边形 $A B C D$ 中， $∠ A = 65^{\circ}$ ，则 $∠ D$ 的度数等于；

查看试题解析
14. ①从装有1个红球和2个黄球的袋子中摸出的1个球恰好是白球；②一副去掉大、小王的扑克牌中，随意抽取1张，抽到的牌是红色的；③站在平地上抛一块小石头，石头会下落；④随意遇到一位青年，他接受过九年制义务教育；以上事件为“不可能事件”的是：；（填序号）

查看试题解析
15. ①掷一枚使币，正面朝上；②如果 $a^{2} = b^{2}$ ，那么 $| a | = | b |$ ；③黑暗中我从一大串钥匙中随便选中一把，用它打开了门；④两条直线被第三条直线所截，同位角相等；⑤在13个人中至少有2人的出生月份相同；以上事件为“必然事件”的是；（填序号）

查看试题解析
16. 在 $▱ A B C D$ 中对角线 $A C$ 、 $B D$ 相交于点 $O$ ，若 $A B = 4$ $A C = 10$ 则 $B D$ 的取值范围；

查看试题解析
17. 若连续抛掷一枚质地均匀的骰子两次得到的点数分别为 $m$ 、 $n$ ，则 $m + n$ 最大值是；

查看试题解析
18. 在等腰直角 $△ A B C$ 中， $∠ C = 90^{\circ}$ ， $B C = 2 c m$ ，如果以 $A C$ 的中点 $D$ 为旋转中心，将这个三角形旋转180°，点 $B$ 落在点 $B^{'}$ 处，则 $D B^{'}$ 的长度为.

查看试题解析

三、解答题

19. 在平行四边形 $A B C D$ 中，已知 $A B = 5$ ，周长为26， $∠ A = 130^{\circ}$ 求其余三边的长及三个内角的度数.

查看试题解析
20. 为了了解某校七年级男生的体能情况，从该校七年级抽取50名男生进行1分钟跳绳测试，把所得数据整理后，画出频数分布直方图.已知图中从左到右第一、第二、第三、第四小组的频数的比为1：3：4：2.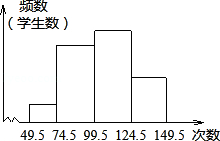

(1)、总体是，个体是，样本容量是；

(2)、求第四小组的频数和频率；

(3)、求所抽取的50名男生中，1分钟跳绳次数在100次以上（含100次）的人数占所抽取的男生人数的百分比.

查看试题解析
21. 如图，平面直角坐标系内，小正方形网格的边长为1个单位长度， $△ A B C$ 的三个顶点的坐标分别为 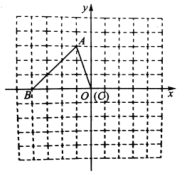$A (- 1 ， 3)$ 、 $B (- 4 ， 0)$ 、 $C (0 ， 0)$ .

①画出将 $△ A B C$ 向上平移1个单位长度，再向右平移5个单位长度后得到的 $△ A_{1} B_{1} C_{1}$

②画出将 $△ A B C$ 绕原点 $O$ 顺时针方向旋转90°得到的 $△ A_{2} B_{2} O$ .

查看试题解析
22. 如图，分别转动甲、乙、丙、丁四个转盘，当转盘停止后，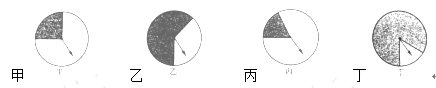

(1)、哪个转盘的指针指向阴影区域的可能性最大？

(2)、哪个转盘的指针指向阴影区域的可能性最小？

(3)、若设 $A$ 、 $B$ 、 $C$ 、 $D$ 分别表示甲、乙、丙、丁四个转盘的指针指向阴影区域，用“<”把指向阴影区域的概率 $P （ A ）$ 、 $P （ B ）$ 、 $P （ C ）$ 、 $P （ D ）$ 连接起来.

查看试题解析
23. 如图，已知： $A B / / D F$ ， $B C / / E D$ ， $A C / / E F$ ，

(1)、图中有几个平行四边形？将它们分别表示出来.

(2)、在（1）中选择一个进行证明.

(3)、证明： $F$ 是 $B C$ 边上的中点.

查看试题解析
24. 某校对八年级学生上学的4种方式：骑车、步行、乘车、接送，进行抽样调查，结果如图（1）、图（2）.

(1)、该抽样调查中样本容量是，其中，步行人数占样本容量的%，骑车人数占样本容量的%，乘车人数占样本容量的%.

(2)、请把条形统计图补充完整；

(3)、根据调查结果，你估计该校八年级500名学生中，大约有多少名学生是由家长接送上学的？

查看试题解析

25. 某商场设立了一个可以自由旋转的转盘，并规定：顾客购物10元以上就能获得一次转动转盘的机会，当转盘停止时，指针落在哪一区域就可以获得相应的奖品.下表是活动进行中的一组落在奖品“铅笔”区域的统计数据：

转动转盘的次数 $n$	100	150	200	500	800	1000
落在“铅笔”的次数 $m$	68	111	136	345	564	701
落在“铅笔”的成功率 $\frac{m}{n}$

(1)、计算并完成表格（精确到0.01）；

(2)、请估计，当

n

很大时，落在“铅笔”区域的频率将会接近（精确到0.1）.

(3)、假如你去转动该转盘一次，你获得铅笔的成功率约是.

查看试题解析

26. 证明：一组对边平行，一组对角相等的四边形是平行四边形.

查看试题解析
27. 如图， $A C$ 、 $B D$ 相交于点 $F$ ， $A B / / C D$ ， $B F = D F$ ， $E$ 、 $G$ 分别是 $A F$ 、 $C F$ 的中点.

(1)、 $B G$ 与 $D E$ 有何关系？

(2)、证明（1）的结论.

查看试题解析