江苏省东台市第三联盟2018-2019学年八年级下学期数学第一次月考试卷
试卷更新日期：2020-03-11 类型：月考试卷
一、单选题
-
1. 下面四个英文大写字母中，既是中心对称图形，又是轴对称图形的是（ ）A、S B、Y C、X D、R2. 下列调查中，适合采用普查方式的是（ ）A、了解我市百岁以上老人的健康情况 B、调查某电视连续剧在全国的收视率 C、了解一批炮弹的杀伤半径 D、了解一批袋装食品是否含有防腐剂3. 下列各式不是分式的是 （ ）A、 B、 C、 D、4. 已知平行四边形ABCD 中，∠B=3∠A，则∠C= （ ）A、18° B、36° C、45° D、135°5. 如图，在△ABC中，AB=5，BC=6，AC=7，点D，E，F分别是△ABC三边的中点，则△DEF的周长为（ ）
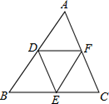A、12 B、11 C、10 D、96. 顺次连结矩形各边的中点所得的四边形是（ ）A、正方形 B、菱形 C、矩形 D、平行四边形7. 某种产品10件，其中有2件次品，其余都是正品，今从中任取一件，抽到次品的可能性为（ ）A、一定 B、不可能 C、可能性较大 D、可能性较小8.如图，E、F分别是正方形ABCD的边CD、AD上的点，且CE=DF，AE、BF相交于点O，下列结论：（1）AE=BF；（2）AE⊥BF；（3）AO=OE；（4） 中正确的有（ ）
A、 4个 B、 3个 C、 2个 D、 1个二、填空题
-
9. 若分式 有意义 ，则 x 的取值范围是若分式 的值为零，则 x 的值10. 袋子里有5只红球，3只白球，每只球除颜色以外都相同，从中任意摸出1只球，是红球的可能性（选填“大于”“小于”或“等于”）是白球的可能性．11. 分式 的最简分母为12. 对某班组织的一次考试成绩进行统计，已知80.5～90.5分这一组的频数是7，频率是0.2，那么该班级的人数是 人．13. 为了掌握我校初中二年级女同学身高情况，从中抽测了 60 名女同学的身高，这个问题中的总体是 ， 样本容量是.14.
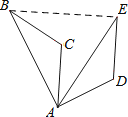
如图，将△ABC绕点A顺时针旋转60°得到△AED ， 若线段AB=3，则BE= ．
15. 矩形的两条对角线的一个交角为 60o ， 两条对角线的长度的和为 8cm，则这个矩形的一条较短边为cm.16. 如图，菱形 ABCD 中，对角线 AC、BD 相交于点O ， H 为 AD 边中点，菱形 ABCD 的周长为 20， 则OH 的长等于.
17.如图，已知菱形ABCD的两条对角线长分别为AC=8和BD=6，那么，菱形ABCD的面积为 ．
18. 如图，在Rt△ABC中， ，AB=3， 点 D在 BC上，以AC为对角线的所有平行四边形ADCE中， DE最小值是 .
三、解答题
-
19. 计算：(1)、 ；(2)、20. 已知：如图，在▱ABCD中，点E、F分别在BC、AD上，且BE＝DF
求证：AC、EF互相平分.
21. 下图是某班学生外出乘车、步行、骑车的人数条形统计图和扇形分布图.
(1)、求该班有多少名学生？(2)、补上步行分布直方图的空缺部分；(3)、在扇形统计图中，求骑车人数所占的圆心角度数.(4)、若全年级有 800 人，估计该年级步行人数.22. 如图，在矩形ABCD中，对角线BD的垂直平分线MN与AD相交于点M，与BC相交于点N，连接BM，DN．
(1)、求证：四边形BMDN是菱形；(2)、若AB=4，AD=8，求MD的长．23. 在△ABC 中，点 M 是边 BC 的中点，AD 平分∠BAC，BD⊥AD，BD 的延长线交 AC 于点 E， AB=12，AC=20.
(1)、求证：BD=DE；(2)、求 DM 的长.24. 已知： ， 求 的值25. 如图，四边形 ABCD 和四边形 DEFG 都是正方形，点E，G 分别在 AD，CD 上，连接 AF， BF，CF.
(1)、求证：AF=CF；(2)、若∠BAF=35°，求∠BFC 的度数.26. 如图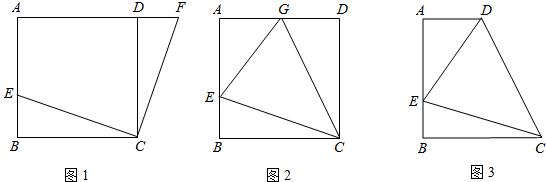
(1)、如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF＝BE，求证：CE＝CF；(2)、如图2，在正方形ABCD中，E是AB上一点，G是AD上一点，如果∠GCE＝45°，请你利用（1）的结论证明：GE＝BE＋GD；(3)、运用（1）（2）解答中所积累的经验和知识，完成下题：如图3，在直角梯形ABCD中，AD∥BC（BC＞AD），∠B＝90°，AB＝BC，E是AB上一点，且∠DCE＝45°，BE＝4，DE=10， 求直角梯形ABCD的面积.