陕西省咸阳市2016-2017学年高二下学期数学期末考试试卷(理科)
试卷更新日期:2017-08-21 类型:期末考试
一、选择题
-
1. 设函数f(x)可导,则 等于( )A、f′(1) B、3f′(1) C、 D、f′(3)2. 复数 =( )A、2+i B、2﹣i C、1+2i D、1﹣2i3. “完成一件事需要分成n个步骤,各个步骤分别有m1 , m2 , …,mn种方法,则完成这件事有多少种不同的方法?”,要解决上述问题,应用的原理是( )A、加法原理 B、减法原理 C、乘法原理 D、除法原理4. 完成一项工作,有两种方法,有5个人只会用第一种方法,另外有4个人只会用第二种方法,从这9个人中选1人完成这项工作,一共有多少种选法?( )A、5 B、4 C、9 D、205. 设X是一个离散型随机变量,则下列不能成为X的概率分布列的一组数据是( )A、0, ,0,0, B、0.1,0.2,0.3,0.4 C、p,1﹣p(0≤p≤1) D、 , ,…,6. 已知随机变量ξ服从正态分布N(2017,σ2),则P(ξ<2017)等于( )A、 B、 C、 D、7. 图中阴影部分的面积用定积分表示为( )
 A、 2xdx B、 (2x﹣1)dx C、 (2x+1)dx D、 (1﹣2x)dx8. 某人有3个电子邮箱,他要发5封不同的电子邮件,则不同的发送方法有( )A、8种 B、15种 C、35种 D、53种9. 盒中装有10个乒乓球,其中6个新球,4个旧球,不放回地依次取出2个球使用,在第一次取出新球的条件下,第二次也取到新球的概率为( )A、 B、 C、 D、10. 函数y=f(x)的图象如图所示,则导函数y=f'(x)的图象可能是( )
A、 2xdx B、 (2x﹣1)dx C、 (2x+1)dx D、 (1﹣2x)dx8. 某人有3个电子邮箱,他要发5封不同的电子邮件,则不同的发送方法有( )A、8种 B、15种 C、35种 D、53种9. 盒中装有10个乒乓球,其中6个新球,4个旧球,不放回地依次取出2个球使用,在第一次取出新球的条件下,第二次也取到新球的概率为( )A、 B、 C、 D、10. 函数y=f(x)的图象如图所示,则导函数y=f'(x)的图象可能是( ) A、
A、 B、
B、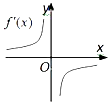 C、
C、 D、
D、 11. 记I为虚数集,设a,b∈R,x,y∈I.则下列类比所得的结论正确的是( )A、由a•b∈R,类比得x•y∈I B、由a2≥0,类比得x2≥0 C、由(a+b)2=a2+2ab+b2 , 类比得(x+y)2=x2+2xy+y2 D、由a+b>0⇒a>﹣b,类比得x+y>0⇒x>﹣y12. 已知函数f(x)在R上可导,且f(x)=x2+2xf′(2),则函数f(x)的解析式为( )A、f(x)=x2+8x B、f(x)=x2﹣8x C、f(x)=x2+2x D、f(x)=x2﹣2x
11. 记I为虚数集,设a,b∈R,x,y∈I.则下列类比所得的结论正确的是( )A、由a•b∈R,类比得x•y∈I B、由a2≥0,类比得x2≥0 C、由(a+b)2=a2+2ab+b2 , 类比得(x+y)2=x2+2xy+y2 D、由a+b>0⇒a>﹣b,类比得x+y>0⇒x>﹣y12. 已知函数f(x)在R上可导,且f(x)=x2+2xf′(2),则函数f(x)的解析式为( )A、f(x)=x2+8x B、f(x)=x2﹣8x C、f(x)=x2+2x D、f(x)=x2﹣2x二、填空题
-
13. 设i为虚数单位,若2+ai=b﹣3i(a、b∈R),则a+bi= .14. 二项式(ax﹣ )3的展开式的第二项系数为﹣ ,则a2的值为 .15. 某同学通过计算机测试的概率为 ,他连续测试3次,且三次测试相互独立,其中恰有1次通过的概率为 .16. 甲、乙、丙三位同学被问到是否去过A,B,C三个城市时,
甲说:我去过的城市比乙多,但没去过B城市;
乙说:我没去过C城市;
丙说:我们三人去过同一城市;
由此可判断乙去过的城市为 .
三、解答题
-
17. 求下列函数的导数:(1)、f(x)=(1+sinx)(1﹣4x);(2)、f(x)= ﹣2x .18. 求满足下列条件的方法种数:(1)、将4个不同的小球,放进4个不同的盒子,且没有空盒子,共有多少种放法?(2)、将4个不同的小球,放进3个不同的盒子,且没有空盒子,共有多少种放法?(最后结果用数字作答)19. 数列{an}满足an+1= (n∈N*),且a1=0,
(Ⅰ)计算a2、a3、a4 , 并推测an的表达式;
(Ⅱ)请用数学归纳法证明你在(Ⅰ)中的猜想.
20. 某学校课题组为了研究学生的数学成绩与学生细心程度的关系,在本校随机调查了100名学生进行研究.研究结果表明:在数学成绩及格的60名学生中有45人比较细心,另15人比较粗心;在数学成绩不及格的40名学生中有10人比较细心,另30人比较粗心.(1)、试根据上述数据完成2×2列联表;数学成绩及格
数学成绩不及格
合计
比较细心
比较粗心
合计
(2)、能否在犯错误的概率不超过0.001的前提下认为学生的数学成绩与细心程度有关系.参考数据:独立检验随机变量K2的临界值参考表:
P(K2≥k0)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k0
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(其中n=a+b+c+d)