山东省2017年春季数学高考试卷

试卷更新日期：2017-08-21 类型：高考模拟

进入出卷网下载

一、选择题

1. 已知全集U={1，2}，集合M={1}，则∁_UM等于（）

A、∅ B、{1} C、{2} D、{1，2}

查看试题解析
2. 函数 $y = \frac{1}{\sqrt{| x | - 2}}$ 的定义域是（）

A、[﹣2，2] B、（﹣∞，﹣2]∪[2，+∞） C、（﹣2，2） D、（﹣∞，﹣2）∪（2，+∞）

查看试题解析
3. 下列函数中，在区间（﹣∞，0）上为增函数的是（）

A、y=x B、y=1 C、 $y = \frac{1}{x}$ D、y=|x|

查看试题解析
4. 二次函数f（x）的图象经过两点（0，3），（2，3）且最大值是5，则该函数的解析式是（）

A、f（x）=2x²﹣8x+11 B、f（x）=﹣2x²+8x﹣1 C、f（x）=2x²﹣4x+3 D、f（x）=﹣2x²+4x+3

查看试题解析
5. 等差数列{a_n}中，a₁=﹣5，a₃是4与49的等比中项，且a₃＜0，则a₅等于（）

A、﹣18 B、﹣23 C、﹣24 D、﹣32

查看试题解析
6. 已知A（3，0），B（2，1），则向量 $\vec{A B}$ 的单位向量的坐标是（）

A、（1，﹣1） B、（﹣1，1） C、 $(- \frac{\sqrt{2}}{2} ， \frac{\sqrt{2}}{2})$ D、 $(\frac{\sqrt{2}}{2} ， - \frac{\sqrt{2}}{2})$

查看试题解析
7. “p∨q为真”是“p为真”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
8. 函数y=cos²x﹣4cosx+1的最小值是（）

A、﹣3 B、﹣2 C、5 D、6

查看试题解析
9. 下列说法正确的是（）

A、经过三点有且只有一个平面 B、经过两条直线有且只有一个平面 C、经过平面外一点有且只有一个平面与已知平面垂直 D、经过平面外一点有且只有一条直线与已知平面垂直

查看试题解析
10. 过直线x+y+1=0与2x﹣y﹣4=0的交点，且一个方向向量 $\vec{v} = (- 1 ， 3)$ 的直线方程是（）

A、3x+y﹣1=0 B、x+3y﹣5=0 C、3x+y﹣3=0 D、x+3y+5=0

查看试题解析
11. 文艺演出中要求语言类节目不能相邻，现有4个歌舞类节目和2个语言类节目，若从中任意选出4个排成节目单，则能排出不同节目单的数量最多是（）

A、72 B、120 C、144 D、288

查看试题解析
12. 若a，b，c均为实数，且a＜b＜0，则下列不等式成立的是（）

A、a+c＜b+c B、ac＜bc C、a²＜b² D、 $\sqrt{- a} < \sqrt{- b}$

查看试题解析
13. 函数f（x）=2^kx ， g（x）=log₃x，若f（﹣1）=g（9），则实数k的值是（）

A、1 B、2 C、﹣1 D、﹣2

查看试题解析
14. 如果 $| \vec{a} | = 3$ ， $\vec{b} = - 2 \vec{a}$ ，那么 $\vec{a} \cdot \vec{b}$ 等于（）

A、﹣18 B、﹣6 C、0 D、18

查看试题解析
15. 已知角α的终边落在直线y=﹣3x上，则cos（π+2α）的值是（）

A、 $\frac{3}{5}$ B、 $\frac{4}{5}$ C、 $\pm \frac{3}{5}$ D、 $\pm \frac{4}{5}$

查看试题解析
16. 二元一次不等式2x﹣y＞0表示的区域（阴影部分）是（）

A、 B、 C、 D、

查看试题解析
17. 已知圆C₁和C₂关于直线y=﹣x对称，若圆C₁的方程是（x+5）²+y²=4，则圆C₂的方程是（）

A、（x+5）²+y²=2 B、x²+（y+5）²=4 C、（x﹣5）²+y²=2 D、x²+（y﹣5）²=4

查看试题解析
18. 若二项式 ${(\sqrt{x} - \frac{1}{x})}^{n}$ 的展开式中，只有第4项的二项式系数最大，则展开式中的常数项是（）

A、20 B、﹣20 C、15 D、﹣15

查看试题解析
19. 从甲、乙、丙、丁四位同学中选拔一位成绩较稳定的优秀选手，参加山东省职业院校技能大赛，在同样条件下经过多轮测试，成绩分析如表所示，根据表中数据判断，最佳人选为（）
成绩分析表

甲
乙
丙
丁
平均成绩 $\bar{x}$
96
96
85
85
标准差s
4
2
4
2

A、甲 B、乙 C、丙 D、丁

查看试题解析
20. 已知A₁ ， A₂为双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ （a＞0，b＞0）的两个顶点，以A₁A₂为直径的圆与双曲线的一条渐近线交于M，N两点，若△A₁MN的面积为 $\frac{a^{2}}{2}$ ，则该双曲线的离心率是（）

A、 $\frac{2 \sqrt{2}}{3}$ B、 $\frac{2 \sqrt{3}}{3}$ C、 $\frac{2 \sqrt{5}}{3}$ D、 $\frac{2 \sqrt{6}}{3}$

查看试题解析

二、填空题：

21. 若圆锥的底面半径为1，母线长为3，则该圆锥的侧面积等于．

查看试题解析
22. 在△ABC中，a=2，b=3，∠B=2∠A，则cosA= ．

查看试题解析
23. 已知F₁ ， F₂是椭圆 $\frac{x^{2}}{16}$ + $\frac{y^{2}}{36}$ =1的两个焦点，过F₁的直线交椭圆于P、Q两点，则△PQF₂的周长等于．

查看试题解析
24. 某博物馆需要志愿者协助工作，若从6名志愿者中任选3名，则其中甲、乙两名志愿者恰好同时被选中的概率是．

查看试题解析
25. 对于实数m，n，定义一种运算： $m * n = {\begin{matrix} m ， m \geq n \\ n ， m < n \end{matrix}$ ，已知函数f（x）=a*a^x ，其中0＜a＜1，若f（t﹣1）＞f（4t），则实数t的取值范围是．

查看试题解析

三、解答题

26. 已知函数f（x）=log₂（3+x）﹣log₂（3﹣x），

(1)、求函数f（x）的定义域，并判断函数f（x）的奇偶性；

(2)、已知f（sinα）=1，求α的值．

查看试题解析
27. 某职业学校的王亮同学到一家贸易公司实习，恰逢该公司要通过海运出口一批货物，王亮同学随公司负责人到保险公司洽谈货物运输期间的投保事宜，保险公司提供了缴纳保险费的两种方案：

①一次性缴纳50万元，可享受9折优惠；
②按照航行天数交纳：第一天缴纳0.5元，从第二天起每天交纳的金额都是其前一天的2倍，共需交纳20天．
请通过计算，帮助王亮同学判断那种方案交纳的保费较低．

查看试题解析
28. 已知直三棱柱ABC﹣A₁B₁C₁的所有棱长都相等，D，E分别是AB，A₁C₁的中点，如图所示．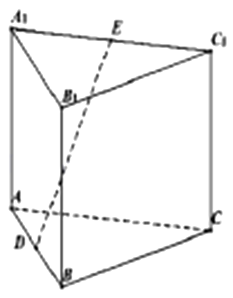

(1)、求证：DE∥平面BCC₁B₁；

(2)、求DE与平面ABC所成角的正切值．

查看试题解析
29. 已知函数 $y = 3 (s i n 2 x c o s \frac{π}{6} - c o s 2 x s i n \frac{π}{6})$ ．

(1)、求该函数的最小正周期；

(2)、求该函数的单调递减区间；

(3)、用“五点法”作出该函数在长度为一个周期的闭区间上的简图．

查看试题解析
30.
已知椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的右焦点与抛物线y²=4x的焦点F重合，且椭圆的离心率是 $\frac{1}{2}$ ，如图所示．

(1)、求椭圆的标准方程；

(2)、抛物线的准线与椭圆在第二象限相交于点A，过点A作抛物线的切线l，l与椭圆的另一个交点为B，求线段AB的长．

查看试题解析

	甲	乙	丙	丁
平均成绩 $\bar{x}$	96	96	85	85
标准差s	4	2	4	2