山东省潍坊市寿光市2016-2017学年高二下学期数学期末考试试卷（文科）

试卷更新日期：2017-08-21 类型：期末考试

进入出卷网下载

一、选择题

1. 已知集合A={1，2，3，4，5}，B=（2，4，6），P=A∩B，则集合P的子集有（）

A、2个 B、4个 C、6个 D、8个

查看试题解析
2. 命题“∀x∈R，x²+1＞0”的否定是（）

A、∀x∈R，x²+1＜0 B、∀x∈R，x²+1≤0 C、∃x∈R，x²+1≤0 D、∃x∈R，x²+1＜0

查看试题解析
3. 函数f（x）= $\sqrt{27 - 3^{x}}$ +log₂（x+2）的定义域为（）

A、（﹣2，3） B、（﹣2，3] C、（0，3） D、（0，3]

查看试题解析
4. 若a=log₃0.6，b=3^0.6 ， c=0.6³ ，则（）

A、c＞a＞b B、a＞b＞c C、b＞c＞a D、a＞c＞b

查看试题解析
5. 函数y=x²+ln|x|的图象大致为（）

A、 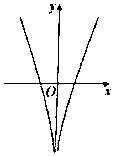B、 C、 D、

查看试题解析
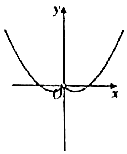6. 设f（x）是R上的任意函数，则下列叙述正确的是（）

A、f（x）f（﹣x）是奇函数 B、f（x）|f（﹣x）|是奇函数 C、f（x）﹣f（﹣x）是偶函数 D、f（x）+f（﹣x）是偶函数

查看试题解析
7. 设a，b∈R，则“log₂a＞log₂b”是“2^a^﹣^b＞1”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
8. 若a＞b＞0，c＜d＜0，则一定有（）

A、 $\frac{a}{c}$ ＞ $\frac{b}{d}$ B、 $\frac{a}{c}$ ＜ $\frac{b}{d}$ C、 $\frac{a}{d}$ ＞ $\frac{b}{c}$ D、 $\frac{a}{d}$ ＜ $\frac{b}{c}$

查看试题解析
9. 设函数f（x）（x∈R）为奇函数，f（1）= $\frac{1}{2}$ ，f（x+2）=f（x）+f（2），则f（﹣5）=（）

A、﹣ $\frac{5}{2}$ B、 $\frac{3}{2}$ C、 $\frac{5}{2}$ D、5

查看试题解析
10. 曲线f（x）=2alnx+bx（a＞0，b＞0）在点（1，f（1））处的切线的斜率为2，则 $\frac{8 a + b}{a b}$ 的最小值是（）

A、10 B、9 C、8 D、3 $\sqrt{2}$

查看试题解析
11. 函数f（x）是定义在R上的偶函数，且满足f（x+2）=f（x）．当x∈[0，1]时，f（x）=2x，若方程ax+a﹣f（x）=0（a＞0）恰有三个不相等的实数根，则实数a的取值范围是（　　）

A、（ $\frac{1}{2}$ ， 1） B、[0，2] C、（1，2） D、[1，+∞）

查看试题解析
12. 定义域为R的可导函数y=f（x）的导函数为f′（x），满足f（x）＞f′（x），且f（0）=3，则不等式f（x）＜3e^x的解集为（）

A、（﹣∞，0） B、（﹣∞，2） C、（0，+∞） D、（2，+∞）

查看试题解析

二、填空题

13. 已知函数f（x）= ${\begin{matrix} l o g_{2} x ， x > 0 \\ 3^{x} ， x \leq 0 \end{matrix}$ 则f（f（ $\frac{1}{4}$ ））= ．

查看试题解析
14. 已知实数x、y满足 ${\begin{matrix} x - y \leq 2 \\ x + y \leq 6 \\ x \geq 0 ， y \geq 0 \end{matrix}$ ，则z=2x+y的最大值是．

查看试题解析
15. 已知函数f（x）=2x²+bx+c，不等式f（x）＜0的解集是（0，5），若对于任意x∈[2，4]，不等式f（x）+t≤2恒成立，则t的取值范围为．

查看试题解析
16. 设曲线y=xⁿ⁺¹（n∈N⁺）在点（1，1）处的切线与x轴的交点的横坐标为x_n ，则log₂₀₁₇x₁+log₂₀₁₇x₂+…+log₂₀₁₇x₂₀₁₆的值为．

查看试题解析

三、解答题

17. 已知全集U=R，集合A={x|1＜2^x＜8}，B={x| $\frac{6}{x - 4}$ +1＜0}，C={x|a＜x＜a+1}．

(1)、求集合∁_UA∩B；

(2)、若B∪C=B，求实数a的取值范围．

查看试题解析
18. 定义在R上的函数y=f（x）对任意的x、y∈R，满足条件：f（x+y）=f（x）+f（y）﹣1，且当x＞0时，f（x）＞1．

(1)、求f（0）的值；

(2)、证明：函数f（x）是R上的单调增函数；

(3)、解关于t的不等式f（2t²﹣t）＜1．

查看试题解析
19. 设某物体一天中的温度T是时间t的函数，已知T（t）=t³+at²+bt+c，其中温度的单位是℃，时间的单位是小时，规定中午12：00相应的t=0，中午12：00以后相应的t取正数，中午12：00以前相应的t取负数（例如早上8：00对应的t=﹣4，下午16：00相应的t=4），若测得该物体在中午12：00的温度为60℃，在下午13：00的温度为58℃，且已知该物体的温度在早上8：00与下午16：00有相同的变化率．

(1)、求该物体的温度T关于时间t的函数关系式；

(2)、该物体在上午10：00至下午14：00这段时间中（包括端点）何时温度最高？最高温度是多少？

查看试题解析
20. 对于函数f（x），若存在x₀∈R，使f（x₀）=x₀ ，则称x₀是f（x）的一个不动点．

(1)、若函数f（x）=2x+ $\frac{4}{x}$ ﹣5，求此函数的不动点；

(2)、若二次函数f（x）=ax²﹣x+3在x∈（1，+∞）上有两个不同的不动点，求实数a的取值范围．

查看试题解析
21. 已知函数f（x）= $\frac{l n x + 1}{e^{x}}$ （e是自然对数的底数），h（x）=1﹣x﹣xlnx．

(1)、求曲线y=f（x）在点A（1，f（1））处的切线方程；

(2)、求h（x）的单调区间；

(3)、设g（x）=xf′（x），其中f′（x）为f（x）的导函数，证明：对任意x＞0，g（x）＜1+e^﹣² ．

查看试题解析
22. 在直角坐标系xOy中，圆C的参数方程 ${\begin{matrix} x = 1 + c o s φ \\ y = s i n φ \end{matrix}$ （φ为参数），以O为极点，x轴的非负半轴为极轴建立极坐标系．

(1)、求圆C的极坐标方程；

(2)、直线l的极坐标方程是2ρsin（θ+ $\frac{π}{3}$ ）=3 $\sqrt{3}$ ，射线OM：θ= $\frac{π}{3}$ 与圆C的交点为O、P，与直线l的交点为Q，求线段PQ的长．

查看试题解析
23. 已知函数f（x）=|x+m|+|2x﹣1|（m∈R）．

(1)、当m=﹣1时，求不等式f（x）≤2的解集；

(2)、设关于x的不等式f（x）≤|2x+1|的解集为A，且[1，2]⊆A，求实数m的取值范围．

查看试题解析