江西省南昌一中、十中、南铁一中联考2016-2017学年高二下学期数学期末考试试卷(理科)
试卷更新日期:2017-08-21 类型:期末考试
一、选择题
-
1. 从集合{0,1,2,3,4,5}中任取两个互不相等的数a,b组成复数a+bi,其中虚数有( )个.A、36 B、30 C、25 D、202. (lg2)20+C201(lg2)19lg5+…+C20r﹣1(lg2)21﹣r(lg5)r﹣1+…+(lg5)20=( )A、1 B、(lg7)20 C、220 D、10203. 一个四面体的顶点在空间直角坐标系O﹣xyz中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx平面为投影面,则得到正视图可以为( )
A、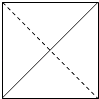 B、
B、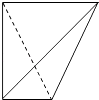 C、
C、 D、
D、 4. 某产品的广告费用x与销售额y的统计数据如下表
4. 某产品的广告费用x与销售额y的统计数据如下表广告费用x(万元)
4
2
3
5
销售额y(万元)
49
26
39
54
根据上表可得回归方程 的 为9.4,据此模型预报广告费用为6万元时销售额为( )
A、63.6万元 B、65.5万元 C、67.7万元 D、72.0万元5. 某学校为了了解该校学生对于某项运动的爱好是否与性别有关,通过随机抽查110名学生,得到如下2×2的列联表:喜欢该项运动
不喜欢该项运动
总计
男
40
20
60
女
20
30
50
总计
60
50
110
由公式K2= ,算得K2≈7.61
附表:
p(K2≥k0)
0.025
0.01
0.005
k0
5.024
6.635
7.879
参照附表,以下结论正确是( )
A、有99.5%以上的把握认为“爱好该项运动与性别有关” B、有99.5%以上的把握认为“爱好该项运动与性别无关” C、有99%以上的把握认为“爱好该项运动与性别有关” D、有99%以上的把握认为“爱好该项运动与性别无关”6. 定义“三角恋写法”为“三个人之间写信,每人给另外两人之一写一封信,且任意两个人不会彼此给对方写信”,若五个人a,b,c,d,e中的每个人都恰给其余四人中的某一个人写了一封信,则不出现“三角恋写法”写法的写信情况的种数为( )A、704 B、864 C、1004 D、10147. 已知三棱柱ABC﹣A1B1C1的侧棱与底面边长都相等,A1在底面ABC上的射影D为BC的中点,则异面直线AB与CC1所成的角的余弦值为( ) A、 B、 C、 D、8. 若x∈(﹣∞,1),则函数y= 有( )A、最小值1 B、最大值1 C、最大值﹣1 D、最小值﹣19. 设x,y∈R,a>1,b>1,若ax=by=2.2a+b=8,则 的最大值为( )A、2 B、3 C、4 D、log2310. 为提高信息在传输中的抗干扰能力,通常在原信息中按一定规则加入相关数据组成传输信息,设定原信息为a0a1a2 , ai∈{0,1}(i=0,1,2),传输信息为h0a0a1a2h1 , 其中h0=a0⊕a1 , h1=h0⊕a2 . ⊕运算规则为:0⊕0=0,0⊕1=1,1⊕0=1,1⊕1=0,例如原信息为111,则传输信息为01111.传输信息在传输过程中受到干扰可能导致接收信息出错,则下列接收信息一定有误的是( )A、10111 B、01100 C、11010 D、0001111. 第一届“一带一路”国际合作高峰论坛于2017年5月14日至15日在北京举行,为了保护各国元首的安全,将5个安保小组全部安排到指定三个区域内工作,且这三个区域每个区域至少有一个安保小组,则这样的安排的方法共有( )A、96种 B、100种 C、124种 D、150种12. 记“点M(x,y)满足x2+y2≤a(a>0)“为事件A,记“M(x,y)满足 ”为事件B,若P(B|A)=1,则实数a的最大值为( )A、 B、 C、1 D、13
A、 B、 C、 D、8. 若x∈(﹣∞,1),则函数y= 有( )A、最小值1 B、最大值1 C、最大值﹣1 D、最小值﹣19. 设x,y∈R,a>1,b>1,若ax=by=2.2a+b=8,则 的最大值为( )A、2 B、3 C、4 D、log2310. 为提高信息在传输中的抗干扰能力,通常在原信息中按一定规则加入相关数据组成传输信息,设定原信息为a0a1a2 , ai∈{0,1}(i=0,1,2),传输信息为h0a0a1a2h1 , 其中h0=a0⊕a1 , h1=h0⊕a2 . ⊕运算规则为:0⊕0=0,0⊕1=1,1⊕0=1,1⊕1=0,例如原信息为111,则传输信息为01111.传输信息在传输过程中受到干扰可能导致接收信息出错,则下列接收信息一定有误的是( )A、10111 B、01100 C、11010 D、0001111. 第一届“一带一路”国际合作高峰论坛于2017年5月14日至15日在北京举行,为了保护各国元首的安全,将5个安保小组全部安排到指定三个区域内工作,且这三个区域每个区域至少有一个安保小组,则这样的安排的方法共有( )A、96种 B、100种 C、124种 D、150种12. 记“点M(x,y)满足x2+y2≤a(a>0)“为事件A,记“M(x,y)满足 ”为事件B,若P(B|A)=1,则实数a的最大值为( )A、 B、 C、1 D、13二、二.填空题
-
13. 已知命题p:“∀x∈R,∃m∈R,使4x+2x•m+1=0”.若命题p为真命题,则实数m的取值范围是 .14. 在某次联考数学测试中,学生成绩η服从正态分布N(100,δ2),(δ>0),若η在(80,120)内的概率为0.6,则落在(0,80)内的概率为 .15. 从装有n+1个球(其中n个白球,1个黑球)的口袋中取出m个球(0<m≤n,m,n∈N),共有 种取法.在这 种取法中,可以分成两类:一类是取出的m个球全部为白球,共有 种取法;另一类是取出的m个球有m﹣1个白球和1个黑球,共有 种取法.显然 ,即有等式: 成立.试根据上述思想化简下列式子: = .16. 下列说法:
①分类变量A与B的随机变量K2越大,说明“A与B有关系”的可信度越大.
②以模型y=cekx去拟合一组数据时,为了求出回归方程,设z=lny,将其变换后得到线性方程z=0.3x+4,则c,k的值分别是e4和0.3.
③根据具有线性相关关系的两个变量的统计数据所得的回归直线方程为y=a+bx中,b=1, =1, =3,
则a=1.正确的序号是 .
三、解答题
-
17. 某幼儿园为训练孩子的数字运算能力,在一个盒子里装有标号为1,2,3,4,5的卡片各两张,让孩子从盒子里任取3张卡片,按卡片上的最大数字的9倍计分,每张卡片被取出的可能性都相等,用X表示取出的3张卡片上的最大数字(1)、求取出的3张卡片上的数字互不相同的概率;(2)、求随机变量X的分布列及数学期望;(3)、若孩子取出的卡片的计分超过30分,就得到奖励,求孩子得到奖励的概率.18. 如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,AD∥BC,CD=13,AB=12,BC=10,AD=5,PD=8,点E,F分别是PB,DC的中点.
 (1)、求证:EF∥平面PAD;(2)、求EF与平面PDB所成角的正弦值.19. 已知 的展开式的各项系数之和等于 展开式中的常数项,求 展开式中含 的项的二项式系数.20. 如图,在底面是菱形的四棱锥P﹣ABCD中,∠ABC=60°,PA=AC=a,PB=PD= ,点E在PD上,且PE:ED=2:1.
(1)、求证:EF∥平面PAD;(2)、求EF与平面PDB所成角的正弦值.19. 已知 的展开式的各项系数之和等于 展开式中的常数项,求 展开式中含 的项的二项式系数.20. 如图,在底面是菱形的四棱锥P﹣ABCD中,∠ABC=60°,PA=AC=a,PB=PD= ,点E在PD上,且PE:ED=2:1.
(Ⅰ)证明PA⊥平面ABCD;
(Ⅱ)求以AC为棱,EAC与DAC为面的二面角θ的大小;
(Ⅲ)在棱PC上是否存在一点F,使BF∥平面AEC?证明你的结论.
21. 某班级举行一次知识竞赛活动,活动分为初赛和决赛两个阶段、现将初赛答卷成绩(得分均为整数,满分为100分)进行统计,制成如下频率分布表.分数(分数段)
频数(人数)
频率
[60,70)
①
0.16
[70,80)
22
②
[80,90)
14
0.28
[90,100)
③
④
合计
50
1
(1)、填充频率分布表中的空格(在解答中直接写出对应空格序号的答案);(2)、决赛规则如下:参加决赛的每位同学依次口答4道小题,答对2道题就终止答题,并获得一等奖.如果前三道题都答错,就不再答第四题.某同学进入决赛,每道题答对的概率P的值恰好与频率分布表中不少于80分的频率的值相同.①求该同学恰好答满4道题而获得一等奖的概率;
②记该同学决赛中答题个数为X,求X的分布列及数学期望.
22. 设不等式﹣2<|x﹣1|﹣|x+2|<0的解集为M,a,b∈M.(Ⅰ)证明:| a+ b|< ;
(Ⅱ)比较|1﹣4ab|与2|a﹣b|的大小.