2015年高考文数真题试卷（新课标Ⅰ卷）

试卷更新日期：2016-04-15 类型：高考真卷

进入出卷网下载

一、选择题：本大题共12小题，每小题5分，在每题给出的四个选项中，只有一项是符合题目要求的

1. 已知集合A={x|-1 $<$ x $<$ 2}，B={x|0 $<$ x $<$ 3}，则A $\cup$ B=（）

A、（-1，3） B、（-1，0） C、（0，2） D、（2，3）

查看试题解析
2. 若a为实数，且 $\frac{2 + a i}{1 + i}$ =3+i，则a=（）

A、-4 B、-3 C、3 D、4

查看试题解析
3.
根据下面给出的2004年至2013年我国二氧化碳年排放量（单位：万吨）柱形图，以下结论中不正确的是（）

A、逐年比较，2008年减少二氧化碳排放量的效果最显著 B、2007年我国治理二氧化碳排放显现成效 C、2006年以来我国二氧化碳年排放量呈减少趋势 D、2006年以来我国二氧化碳年排放量与年份正相关

查看试题解析
4. 已知a=（1，-1），b=（-1,2），则（2a+b） $\cdot$ a=（）

A、-1 B、0 C、1 D、2

查看试题解析
5. 设S_n是等差数列{a_n}的前n项和，若a₁+a₃+a₅=3，则S₅=（）

A、5 B、7 C、9 D、11

查看试题解析
6.
一个正方体被一个平面截去一部分后，剩余部分的三视图如下图，则截去部分体积与剩余部分体积的比值为（）

A、 $\frac{1}{8}$ B、 $\frac{1}{7}$ C、 $\frac{1}{6}$ D、 $\frac{1}{5}$

查看试题解析
7. 已知三点 $A (1 ， 0) ， B (0 ， \sqrt{3}) ， C (2 ， \sqrt{3})$ ，则 $△ A B C$ 外接圆的圆心到原点的距离为（）

A、 $\frac{5}{3}$ B、 $\frac{\sqrt{21}}{3}$ C、 $\frac{2 \sqrt{5}}{3}$ D、 $\frac{4}{3}$

查看试题解析
8.
下边程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”，执行该程序框图，若输入的a，b 分别为14，18，则输出的a 为（）

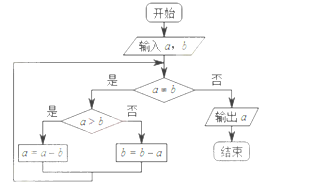A、0 B、2 C、4 D、14

查看试题解析
9. 已知等比数列{a_n}满足a₁= $\frac{1}{4}$ ， a₃a₅=4（a₄-1），则a₂=（）

A、2 B、1 C、 $\frac{1}{2}$ D、 $\frac{1}{8}$

查看试题解析
10. 已知A，B是球O的球面上两点， $∠$ AOB=90 $°$ ， C为该球面上的动点，若三棱锥O-ABC体积的最大值为36，则球O的表面积为（）

A、36 $π$ B、64 $π$ C、144 $π$ D、256 $π$

查看试题解析
11.
如图，长方形的边AB=2，BC=1，O是AB的中点，点P沿着边BC，CD与DA运动，记 $∠$ BOP=x，将动点P到A，B两点距离之和表示为x的函数f（x），则图像大致为（）

A、 B、 C、 D、

查看试题解析
12. 设函数f（x）=ln（1+|x|）- $\frac{1}{1 + x^{2}}$ ，则使得f（x） $>$ f（2x-1）成立的x的取值范围是（）

A、（ $\frac{1}{3}$ ， 1） B、（- $\infty$ ， $\frac{1}{3}$ ） $\cup$ （1，+ $\infty$ ） C、（- $\frac{1}{3}$ ， $\frac{1}{3}$ ） D、（- $\infty$ ， - $\frac{1}{3}$ ） $\cup$ （ $\frac{1}{3}$ ， + $\infty$ ）

查看试题解析

二、填空题：本大题共4小题，每小题5分

13. 已知函数f(x)=ax³-2x的图像过点（-1，4），则a= .

查看试题解析
14.
若x，y满足约束条件{ $\begin{matrix} x + y - 5 \leq 0 \\ 2 x - y - 1 \geq 0 \\ x - 2 y + 1 \leq 0 \end{matrix}$ ，则z=2x+y的最大值为。

查看试题解析
15. 已知双曲线过点（4， $\sqrt{3}$ ），且渐近线方程为y= $\pm$ $\frac{1}{2}$ x，则该双曲线的标准方程为。

查看试题解析
16. 已知曲线y=x+lnx在点（1，1）处的切线与曲线y=ax²+（a+2）x+1相切，则a= 。

查看试题解析

三、解答题

17. $△$ ABC中 D是BC上的点，AD评分 $∠$ BAC，BD=2DC

(1)、(I)求 $\frac{\sin ∠ B}{\sin ∠ C}$

(2)、（II）若 $∠ B A C$ =60 $°$ ，求 $∠$ B

查看试题解析
18.
某公司为了了解用户对其产品的满意度，从A ， B两地区分别随机调查了40个用户，根据用户对其产品的满意度的评分，得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频率分布表.A地区用户满意度评分的频率分布直方图
B地区用户满意度评分的频率分布表
满意度评分分组
[50，60)
[50，60)
[50，60)
[50，60)
[50，60)
频数
2
8
14
10
6

(1)、
（I）在答题卡上作出B地区用户满意度评分的频率分布直方图，并通过此图比较两地区满意度评分的平均值及分散程度.（不要求计算出具体值，给出结论即可）
B地区用户满意度评分的频率分布直方图

(2)、（II）根据用户满意度评分，将用户的满意度评分分为三个等级：
满意度评分
低于70分
70分到89分
不低于90分
满意度等级
不满意
满意
非常满意
估计那个地区的用户的满意度等级为不满意的概率大，说明理由.

查看试题解析
19.
如图，长方体ABCD-A₁B₁C₁D₁中，AB=16，BC=10，AA₁=8，点E，F分别在A₁B_1，D₁C_1上，A₁E=D₁F=4.过点E，F的平面 $α$ 与此长方体的面相交，交线围成一个正方形。

(1)、（I）在图中画出这个正方形（不必说明画法与理由）；

(2)、（II）求平面把该长方体分成的两部分体积的比值.

查看试题解析
20. 已知椭圆C： $\frac{x^{2}}{a^{2}}$ + $\frac{y^{2}}{b^{2}}$ =1,(a $>$ b $>$ 0)的离心率为 $\frac{\sqrt{2}}{2}$ ，点（2， $\sqrt{2}$ ）在C上

(1)、求C的方程；

(2)、直线l不经过原点O,且不平行于坐标轴,l与C有两个交点A,B,线段AB中点为M,证明：直线OM的斜率与直线l的斜率乘积为定值.

查看试题解析
21. 已知f（x）=lnx+a（1-x），问：（1）讨论f（x）的单调性；（2）当 f（x）有最大值，且最大值大于2a-2 时，求a的取值范围.

(1)、讨论f（x）的单调性；

(2)、当 f（x）有最大值，且最大值大于2a-2 时，求a的取值范围.

查看试题解析
22.
如图O是等腰三角形ABC内一点，圆O与△ABC的底边BC交于M ， N两点，与底边上的高交于点G ，且与AB ， AC分别相切于E ， F两点.

(1)、(I)证明EF//BC

(2)、(II)若AG等于圆O半径，且AE=MN=2 $\sqrt{3}$ ，求四边形EBCF的面积

查看试题解析
23. 在直角坐标系xO_y中，曲线C₁： $\{\begin{matrix} x = t \cos α \\ y = t \sin α \end{matrix}$ (t为参数，且t≠0)，其中0 $\leq$ $α$ $< π$ ，在以O为极点x轴正半轴为极轴的极坐标系中，曲线C_2：： $ρ$ =2sin $θ$ ， C₃： $ρ$ =2 $\sqrt{3}$ cos $θ，求解下列问题：$

(1)、求C₂与C₃交点的直角坐标

(2)、若C₁与C₂相交于点A，C₁与C₃相交于点B，求|AB|最大值

查看试题解析
24. 设a，b，c，d均为正数，且a+b=c+d，证明：（1）若ab > cd，则 $\sqrt{a}$ + $\sqrt{b}$ > $\sqrt{c}$ + $\sqrt{d}$ ；（2） $\sqrt{a}$ + $\sqrt{b}$ > $\sqrt{c}$ + $\sqrt{d}$ 是|a-b| < |c-d|的充要条件

(1)、（I）若ab $>$ cd，则 $\sqrt{a}$ + $\sqrt{b}$ $>$ $\sqrt{c}$ + $\sqrt{d}$

(2)、(II) $\sqrt{a}$ + $\sqrt{b}$ $>$ $\sqrt{c}$ + $\sqrt{d}$ 是|a-b| $<$ |c-d|的充要条件

查看试题解析

满意度评分分组	[50，60)	[50，60)	[50，60)	[50，60)	[50，60)
频数	2	8	14	10	6

满意度评分	低于70分	70分到89分	不低于90分
满意度等级	不满意	满意	非常满意