初中数学人教版八年级下学期 第十七章测试卷
试卷更新日期:2020-03-10 类型:单元试卷
一、单选题
-
1. 三角形各边长度如下,其中不是直角三角形的是( )A、3,4,5 B、6,8,10 C、5,11,12 D、8,15,172. 在 Rt△ABC 中, ∠C = 90° , AB = 3 , AC = 2, 则 BC 的值( )A、 B、 C、 D、3. 如图,在△ABC中,AB=AC=5,BC=8,点P是BC边上的动点,过点P作PD⊥AB于点D,PE⊥AC于点E,则PD+PE的长是( )
 A、4.8 B、4.8或3.8 C、3.8 D、54. 如图,开口玻璃罐长、宽、高分别为16、6和6,在罐內点E处有一小块饼干碎末,此时一只蚂蚁正好在罐外长方形ABCD的中心H处,蚂蚁到达饼干的最短距离是多少( )
A、4.8 B、4.8或3.8 C、3.8 D、54. 如图,开口玻璃罐长、宽、高分别为16、6和6,在罐內点E处有一小块饼干碎末,此时一只蚂蚁正好在罐外长方形ABCD的中心H处,蚂蚁到达饼干的最短距离是多少( )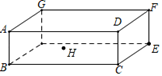 A、 B、17 C、 D、5. 如图,点A坐标为(3,0),B是y轴正半轴上一点,AB=5,则点B的坐标为( )
A、 B、17 C、 D、5. 如图,点A坐标为(3,0),B是y轴正半轴上一点,AB=5,则点B的坐标为( )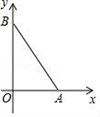 A、(4,0) B、(0,4) C、(0,5) D、(0, )6. 如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为( )
A、(4,0) B、(0,4) C、(0,5) D、(0, )6. 如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为( )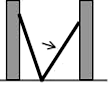 A、2.2米 B、2.3米 C、2.4米 D、2.5米7. 如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为( ).
A、2.2米 B、2.3米 C、2.4米 D、2.5米7. 如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为( ).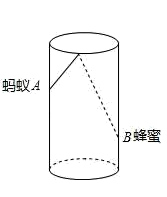 A、13cm B、 cm C、2 cm D、20cm
A、13cm B、 cm C、2 cm D、20cm二、填空题
-
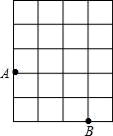
8. 一艘轮船以16km/h的速度离开港口向东北方向航行,另一艘轮船同时离开港口以12km/h的速度向东南方向航行,它们离开港口半小时后相距km9. 如图,A、B是网格中的两个格点,点C也是网格中的一个格点,连接AB、BC、AC,当△ABC为等腰三角形时,设网格中的每个小正方形的边长为1,则所有满足题意的等腰三角形ABC的面积之和等于 .
 10. 如图,一架15m长的梯子AB斜靠在一竖直的墙OA上,这时梯子的顶端A离地面距离OA为12m,如果梯子顶端A沿墙下滑3m至C点,那么梯子底端B向外移至D点,则BD的长为m.
10. 如图,一架15m长的梯子AB斜靠在一竖直的墙OA上,这时梯子的顶端A离地面距离OA为12m,如果梯子顶端A沿墙下滑3m至C点,那么梯子底端B向外移至D点,则BD的长为m.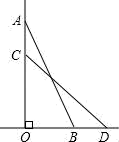 11. 如图,已知所有的四边形都是正方形,所有的三角形都是直角三角形,其中A,B,C,D四个小正方形的面积之和等于8,则最大正方形的边长为 .
11. 如图,已知所有的四边形都是正方形,所有的三角形都是直角三角形,其中A,B,C,D四个小正方形的面积之和等于8,则最大正方形的边长为 .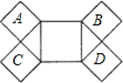 12. 如图所示,“赵爽弦图”是由8个全等的直角三角形拼接而成的,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为 ,已知 ,则 的值是.
12. 如图所示,“赵爽弦图”是由8个全等的直角三角形拼接而成的,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为 ,已知 ,则 的值是.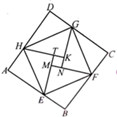 13. 如图,要为一段高为5米,长为13米的楼梯铺上红地毯,则红地毯至少要米长.
13. 如图,要为一段高为5米,长为13米的楼梯铺上红地毯,则红地毯至少要米长.
三、解答题
-
14. 如图在四边形ABCD中, AD=1,AB=BC=2,DC=3,AD⊥AB,求

四、综合题
-
15. 如图,在边长为1的小正方形组成的网格中,四边形ABCD的四个顶点都在格点上,请按要求完成下列各题:
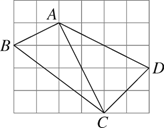 (1)、线段AB的长为 , BC的长为 , CD的长为;(2)、连接AC,通过计算说明△ACD和△ABC各是什么特殊三角形.16. 一块长方体木块的各棱长如图所示,一只蜘蛛在木块的一个顶点A处,一只苍蝇在这个长方体上和蜘蛛相对的顶点B处,蜘蛛急于捉住苍蝇,沿着长方体的表面向上爬.
(1)、线段AB的长为 , BC的长为 , CD的长为;(2)、连接AC,通过计算说明△ACD和△ABC各是什么特殊三角形.16. 一块长方体木块的各棱长如图所示,一只蜘蛛在木块的一个顶点A处,一只苍蝇在这个长方体上和蜘蛛相对的顶点B处,蜘蛛急于捉住苍蝇,沿着长方体的表面向上爬. (1)、如果D是棱的中点,蜘蛛沿“AD→DB”路线爬行,它从A点爬到B点所走的路程为多少?(2)、若蜘蛛还走前面和右面这两个面,你认为“AD-DB"是最短路线吗?如果不是,请求出最短路程,如果是,请说明理由
(1)、如果D是棱的中点,蜘蛛沿“AD→DB”路线爬行,它从A点爬到B点所走的路程为多少?(2)、若蜘蛛还走前面和右面这两个面,你认为“AD-DB"是最短路线吗?如果不是,请求出最短路程,如果是,请说明理由
-