陕西省西安市莲湖区2019-2020学年七年级上学期数学期末考试试卷
试卷更新日期:2020-03-10 类型:期末考试
一、选择题(共10小题,每小题3分,共30分。)
-
1. 6的相反数是( )A、 6 B、 C、-6 D、2. 方程2x-4=-2x+4的解是( )A、x=2 B、x=-2 C、x=1 D、x=03. 在下列几何体中,从正面看到的平面图形为三角形的是( )A、
 B、
B、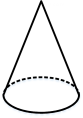 C、
C、 D、
D、 4. 下列运算中,正确的是( )A、2x2+3x2=5x4 B、3x+2y=5xy C、7x2-4x2=3 D、5a2b-4a2b=a2b5. 如图,若x为最小正整数,则表示x- 的值的点落在( )
4. 下列运算中,正确的是( )A、2x2+3x2=5x4 B、3x+2y=5xy C、7x2-4x2=3 D、5a2b-4a2b=a2b5. 如图,若x为最小正整数,则表示x- 的值的点落在( ) A、段① B、段② C、段③ D、段④6. ∠AOB的大小可由量角器测得(如右图所示),则180°-∠AOB的大小为( )
A、段① B、段② C、段③ D、段④6. ∠AOB的大小可由量角器测得(如右图所示),则180°-∠AOB的大小为( )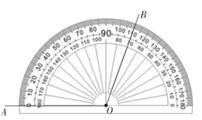 A、0° B、70° C、110° D、180°7. 下列调查方式,你认为最合适的是( )A、为了了解同学们对央视《主持人大赛》栏目的喜爱程度,小华在学校随机采访了10名七年级学生 B、咸阳机场对旅客上飞机进行安检,采用抽样调查方式 C、为了了解西安市七年级学生的身高情况,采用全面调查方式 D、为了了解我省居民的日平均用电量,采用抽样调查方式8. 已知线段AB=12cm,C是AB的中点,在线段AB上有一点D,且CD=2cm。则AD的长是( )A、8cm B、8cm或2cm C、8cm或4cm D、2cm或4cm9. 在公元前4世纪的印度巴克沙利手稿中记载着一题:甲乙丙丁四人各持金,乙为甲的二倍,丙为乙的三倍,丁为丙的四倍,并知四人总持金数为132卢比,则乙的持金数为( )A、4卢比 B、8卢比 C、12卢比 D、16卢比10. 如图,从左到右在每个小格子中都填入一个整数,使得其任意三个相邻格子中所填整数之和都相等,则第2020个格子中的数为( )
A、0° B、70° C、110° D、180°7. 下列调查方式,你认为最合适的是( )A、为了了解同学们对央视《主持人大赛》栏目的喜爱程度,小华在学校随机采访了10名七年级学生 B、咸阳机场对旅客上飞机进行安检,采用抽样调查方式 C、为了了解西安市七年级学生的身高情况,采用全面调查方式 D、为了了解我省居民的日平均用电量,采用抽样调查方式8. 已知线段AB=12cm,C是AB的中点,在线段AB上有一点D,且CD=2cm。则AD的长是( )A、8cm B、8cm或2cm C、8cm或4cm D、2cm或4cm9. 在公元前4世纪的印度巴克沙利手稿中记载着一题:甲乙丙丁四人各持金,乙为甲的二倍,丙为乙的三倍,丁为丙的四倍,并知四人总持金数为132卢比,则乙的持金数为( )A、4卢比 B、8卢比 C、12卢比 D、16卢比10. 如图,从左到右在每个小格子中都填入一个整数,使得其任意三个相邻格子中所填整数之和都相等,则第2020个格子中的数为( )-2 a b c 3 -1 …… A、3 B、-1 C、2 D、-2二、填空题(共4小题,每小题3分,共12分)
-
11. 若单项式 x2ya与-2xby5的和仍为单项式,则ab=。12. 如图,按图中的程序进行计算,如果输入的数是-2,那么输出的数是。
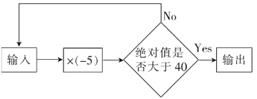 13. 某一时刻闹钟的时针和分针的夹角是108000“,此时这个夹角等于。14. 如图,有一种电子游戏,电子屏幕上有一条直线,在直线上有A,B,C,D四点,且AB=BC= CD,点P沿直线l从右向左移动,当出现点P与A,B,C,D四点中的至少两个点距离相等时,就会发出警报,则直线l上会发出警报的点P有个。
13. 某一时刻闹钟的时针和分针的夹角是108000“,此时这个夹角等于。14. 如图,有一种电子游戏,电子屏幕上有一条直线,在直线上有A,B,C,D四点,且AB=BC= CD,点P沿直线l从右向左移动,当出现点P与A,B,C,D四点中的至少两个点距离相等时,就会发出警报,则直线l上会发出警报的点P有个。
三、解答题(共11小题,共78分。)
-
15. 计算-13-3×(-2)2÷( )16. 解方程17. 先化简,再求值:2a+2(a-b)-(3a-2b)+b,其中a=-2,b=5。18.(1)、如图,已知三点A,B,C,按要求画图:画直线AB;画射线AC;画线段BC。
 (2)、如图,用适当的语句表述点A,P与直线l的关系
(2)、如图,用适当的语句表述点A,P与直线l的关系 19. 如图,在一个正方体的平面展开图中每面标有不同的数字,若将平面展开图折叠成正方体后,相对面上的两个数字之和均为5,求x+y+z的值。
19. 如图,在一个正方体的平面展开图中每面标有不同的数字,若将平面展开图折叠成正方体后,相对面上的两个数字之和均为5,求x+y+z的值。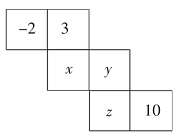 20.(1)、如图,下面两个圈分别表示负数集和分数集,请你把下列各数填入它所在数集的圈里。
20.(1)、如图,下面两个圈分别表示负数集和分数集,请你把下列各数填入它所在数集的圈里。3.4 ,-15% , 0 , , -5 , 3
 (2)、上图中,这两个圈的重叠部分表示什么数集合?(3)、列式并计算:在(1)的数据中,求最大的数与最小的数的和。21. 如图,A,B,C三棵树在同一直线上,若小明正好站在线段AC的中点Q处,BC=2BQ。
(2)、上图中,这两个圈的重叠部分表示什么数集合?(3)、列式并计算:在(1)的数据中,求最大的数与最小的数的和。21. 如图,A,B,C三棵树在同一直线上,若小明正好站在线段AC的中点Q处,BC=2BQ。 (1)、填空:AQ==AC,AQ-BC=。(2)、若BQ=3米,求AC的长。22. 如图,已知射线OC在∠AOB内,OM和ON分别平分∠AOC和∠BOC。
(1)、填空:AQ==AC,AQ-BC=。(2)、若BQ=3米,求AC的长。22. 如图,已知射线OC在∠AOB内,OM和ON分别平分∠AOC和∠BOC。 (1)、若∠AOC=50°,∠BOC=30°,求∠MON的度数。(2)、探究∠MON与∠AOB的数量关系。23. 某校为了组织一次球类对抗赛,在本校随机抽取了若干名学生,对他们每个人最喜欢的一项球类运动进行了统计,将调查结果整理后绘制成如图所示的不完整的统计图,请你依据图中的信息回答下列问题:
(1)、若∠AOC=50°,∠BOC=30°,求∠MON的度数。(2)、探究∠MON与∠AOB的数量关系。23. 某校为了组织一次球类对抗赛,在本校随机抽取了若干名学生,对他们每个人最喜欢的一项球类运动进行了统计,将调查结果整理后绘制成如图所示的不完整的统计图,请你依据图中的信息回答下列问题: (1)、求本次被调查的学生人数。(2)、通过计算补全条形统计图。(3)、若全校有4000名学生,请你估计该校最喜欢篮球和足球运动的学生共有多少人?24. 小方家的住房户型呈长方形,平面图如下(单位:米).现准备铺设地面,其中三间卧室的地面铺设木地板,其他区域的地面铺设地砖。
(1)、求本次被调查的学生人数。(2)、通过计算补全条形统计图。(3)、若全校有4000名学生,请你估计该校最喜欢篮球和足球运动的学生共有多少人?24. 小方家的住房户型呈长方形,平面图如下(单位:米).现准备铺设地面,其中三间卧室的地面铺设木地板,其他区域的地面铺设地砖。 (1)、求a的值。(2)、问铺设地面需要木地板和地砖各多少平方米?(用含x的代数式表示)(3)、按市场价格,木地板价格为300元/平方米,地砖价格为100元/平方米,装修公司有A,B两种活动方案,如表所示:
(1)、求a的值。(2)、问铺设地面需要木地板和地砖各多少平方米?(用含x的代数式表示)(3)、按市场价格,木地板价格为300元/平方米,地砖价格为100元/平方米,装修公司有A,B两种活动方案,如表所示:活动方案
本地板价格
地砖价格
总安装费
A
8折
8.5折
2000元
B
9折
8.5折
免费
已知卧室2的面积为21平方米,则小方家应选择哪种活动方案,可使铺设地面的总费用(含材料费及安装费)更低?请说明理由。
25. 阅读理解:若A,B,C为数轴上的三点,且点C到点A的距离是点C到点B的距离的2倍,我们就称点C是【A,B】的好点。

例如,如图1,点A表示的数为-1,点B表示的数为2,表示1的点C到点A的距离是2,到点B的距离是1,那么点C是【A,B】的好点,又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D就不是【A,B】的好点,但点D是【B,A】的好点。
知识运用:
(1)、如图2,M,N为数轴上的两点,点M所表示的数为-2,点N所表示的数为4.①在点M和点N中间,数所表示的点是【M,N】的好点;
②在数轴上,数和数所表示的点都是【N,M】的好点。
(2)、如图3,A,B为数轴上的两点,点A所表示的数为-20,点B所表示的数为40.现有一只电子蚂蚁P从点B出发,以每秒4个单位长度的速度向左运动,到达点A时停止,则经过几秒后,P,A和B中恰有一个点为其余两点的好点?