广西南宁市2019-2020学年八年级上学期数学期末考试试卷

试卷更新日期：2020-03-10 类型：期末考试

进入出卷网下载

一、选择题(共12小题，每小题3分，共36分．)

1. 下列图形是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 芯片是手机、电脑等高科技产品的核心部件，目前我国芯片已可采用14纳米工艺，已知14纳米为0.000000014米，数据0.000000014科学记数法表示为（）

A、1.4×10^-10 B、1.4×10^-8 C、14×10^-8 D、1.4×10^-9

查看试题解析
3. 在平面直角坐标系中，点A(-3，2)关于x轴的对称点坐标为（）

A、(2，-3) B、(3，2) C、(3，-2) D、(-3，-2)

查看试题解析
4. 如图，窗户打开后，用窗钩AB可将其固定，其所运用的几何原理是（）

A、三角形的稳定性 B、垂线段最短 C、两点确定一条直线 D、两点之间，线段最短

查看试题解析
5. 下列长度的三条线段能组成三角形的是（）

A、2cm， 3cm， 6cm B、3cm， 4cm， 7cm C、5cm， 6cm， 8cm D、7cm， 8cm， 16cm

查看试题解析
6. 将一副三角板按如图所示的方式放置，则∠CAF的大小为（）

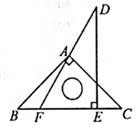A、50° B、60° C、75° D、85°

查看试题解析
7. 若把分式 $\frac{x}{x + y}$ 中的x和y都扩大5倍，则分式的值（）

A、扩大到原来的5倍 B、不变 C、缩小为原来的 $\frac{1}{5}$ 倍 D、扩大到原来的25倍

查看试题解析
8. 下列运算中正确的是

A、x²·x²=2x⁴ B、(ab)²=ab² C、(-x²)³=-x⁶ D、6x²·3xy=9x³y

查看试题解析
9. 工人师傅常用角尺平分一个角，具体做法如下：如图，在∠AOB的边OA，OB上分别取OM=ON，移动角尺，使角尺两边相同的刻度分别与点M，N重合，则过角尺顶点P的射线OC便是∠AOB的平分线，其中证明△MOP≌△NOP时运用的判定定理是（）

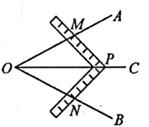A、SSS B、SAS C、ASA D、AAS

查看试题解析
10. 两个工程队共同参与一项筑路工程，甲队单独施工1个月完成总工程的 $\frac{1}{3}$ ，这时增加了乙队，两队又共同工作了半个月，总工程全部完成，如果乙队单独完成总工程需多少个月？设乙队单独完成总工程需x个月，则下列方程正确的是（）

A、 $\frac{1}{3} + \frac{1}{2} + \frac{1}{x} = 1$ B、 $\frac{1}{3} + \frac{1}{6} + \frac{1}{x} = 1$ C、 $\frac{1}{3} + \frac{1}{2} + \frac{1}{2 x} = 1$ D、 $\frac{1}{3} + \frac{1}{2} (\frac{1}{3} + \frac{1}{x}) = 1$

查看试题解析
11. 观察下面的变形规律 $\frac{1}{1 \times 2} = 1 - \frac{1}{2}$ ， $\frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3}$ ， $\frac{1}{3 \times 4} = \frac{1}{3} - \frac{1}{4}$ ， $\frac{1}{4 \times 5} = \frac{1}{4} - \frac{1}{5}$ ，……回答问题：若 $\frac{1}{(x + 1) (x + 2)} + \frac{1}{(x + 2) (x + 3)} + \frac{1}{(x + 3) (x + 4)} + ...... + \frac{1}{(x + 99) (x + 100)} = \frac{1}{x + 100}$ ，则x的值为（）

A、100 B、98 C、1 D、 $\frac{1}{2}$

查看试题解析
12. 如图，在△ABC中，AB=AC，AC的垂直平分线交AC于点N，交AB于点M，AB=12cm，△BMC的周长是20cm．若点P在直线MN上，则PA-PB的最大值为（）

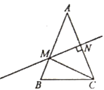A、12cm B、8cm C、6cm D、2cm

查看试题解析

二、填空题(本大题共6小题，每小题3分，共18分)

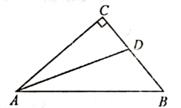
13. 计算：x⁵÷x³= ．

查看试题解析
14. 一个多边形的每个外角都等于60°，则这个多边形的边数是。

查看试题解析
15. 分解因式：4x²+2x=。

查看试题解析
16. 如图，在Rt△ABC中，∠C=90°，∠BAC的平分线AD交BC于点D．若CD=3，AB=8则△ABD的面积是。

查看试题解析
17. 已知2^x=a，32^y=b，x，y为正整数，则2^3x+10y= 。

查看试题解析
18. 如图，图1是一个四边形纸条ABCD，其中AB∥CD，E，F分别为边AB，CD上的两点，且∠BEF=27°，将纸条ABCD沿EF所在直线折叠得到图2，再将图2中的四边形BCFM沿DF所在直线折叠得到图3，则图3中∠EFC的度数为度。

查看试题解析

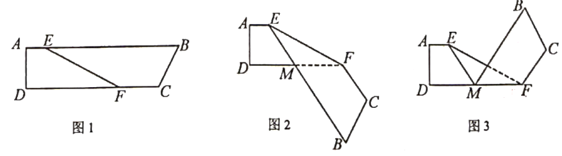
三、解答题(本大题共8小题，共66分．)

19. 计算：2019⁰-( $\frac{1}{3}$ )^-1+2³÷(-2)²

查看试题解析
20. 先化简，再求值： $\frac{a^{2} - a}{a^{2} - 4 a + 4} \times (1 - \frac{1}{a - 1})$ ，其中a=4

查看试题解析
21. 如图，△ABC三个顶点的坐标分别为A(1，2)，B(3，0)，C(5，3)。

(1)、①请画出△ABC向下平移4个单位长度后得△A₁B₁C₁；
②请画出△ABC关于y轴对称的△A₂B₂C₂；

(2)、若坐标轴上存在点M，使得△A₂B₂M是以A₂B₂为底边的等腰三角形，请直接写出满足条件的点M坐标。

查看试题解析
22. 如图，点A、E、F、C在同一直线上，DE∥BF，DE=BF，AE=CF。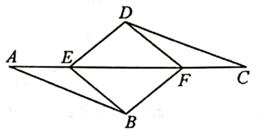

(1)、证明：△ABF≌△CDE；

(2)、若DE=DF=CF，且∠A=20°，求∠EDF的度数。

查看试题解析
23. 某商场计划购进甲、乙两种玩具，已知甲种玩具的单价与乙种玩具的单价和为40元，用900元购得甲种玩具的件数与用1500元购得乙种玩具的件数相同．求甲种、乙种玩具的单价各是多少元？

查看试题解析
24. 如图，在△ABC中，∠ABC=90°，BA=BC，点A在x轴上，点B坐标为(0，-2)。

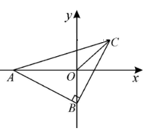(1)、求点C到y轴的距离；

(2)、连接OC，当∠AOC=135°时，求点C的坐标；

(3)、在(2)的条件下，猜想线段OA和线段OB的数量关系，并说明理由。

查看试题解析
25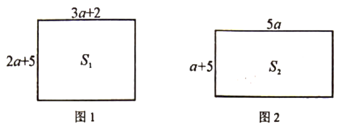. 阅读下列材料：

利用完全平方公式，可以将多项式x²+bx+c变形为(x+m)²+n的形式。

例如：x²-8x+17=x²-2·x·4+4²-4²+17=(x-4)²+1

(1)、填空：将多项式x²-2x+3变形为(x+m)²+n的形式，并判断x²-2x+3与0的大小关系
因为x²-2x+3=(x-)2+

所以x²-2x+30(填“>”、“<”、“≥”、“≤”、“=”)；

(2)、如图1所示的长方形边长分别是2a+5，3a+2，求长方形面积S₁(用含a的式子表示)；如图2所示的长方形边长分别是5a，a+5，求长方形的面积为S₂(用含a的式子表示)

(3)、比较(2)中S₁与S₂的大小，并说明理由。

查看试题解析
26. 在等边△ABC中，点O在BC边上，点D在AC的延长线上，且OA=OD。

(1)、如图1，若点O为BC中点，求∠COD的度数；

(2)、如图2，若点O为BC上的任意一点，求证：AD=AB+BO；

(3)、如图3，若点O为BC上的任意一点，点D关于直线BC的对称点为点P，连接AP，OP，请判断△AOP的形状，并说明理由。

查看试题解析