辽宁省鞍山市铁西2019届九年级下学期数学3月月考试卷

试卷更新日期：2020-03-10 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列几何体中，主视图和左视图都是矩形的是（）

A、 B、 C、 D、

查看试题解析
2. π、 $\frac{22}{7}, - \sqrt{3}, \sqrt[3]{343}, 3.1416, 0.3$ 中，无理数的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 下列运算中，正确的是（）

A、 $a^{3} {(- 3 a)}^{2} = 6 a^{5}$ B、 $a^{3} \div a \cdot \frac{1}{a} = a^{3}$ C、 ${(- 2 a - 1)}^{2} = 4 a^{2} + 4 a + 1$ D、 $2 a^{2} + 3 a^{3} = 5 a^{5}$

查看试题解析
4. 关于 $x$ 的一元二次方程 $(m - 1) x^{2} - 2 x - 1 = 0$ 有两个实数根，则实数 $m$ 的取值范围是（）

A、 $m \geq 0$ B、 $m > 0$ C、 $m > 0$ 且 $m \neq 1$ D、 $m \geq 0$ 且 $m \neq 1$

查看试题解析
5. 某公司今年销售一种产品，一月份获得利润10万元，由于产品畅销，利润逐月增加，一季度共获利36.4万元，已知2月份和3月份利润的月增长率相同．设2，3月份利润的月增长率为x，那么x满足的方程为（）

A、10（1+x）²=36.4 B、10+10（1+x）²=36.4 C、10+10（1+x）+10（1+2x）=36.4 D、10+10（1+x）+10（1+x）²=36.4

查看试题解析
6. 三角形两边长分别为3和6，第三边的长是方程x²﹣13x+36=0的两根，则该三角形的周长为（　　）

A、13 B、15 C、18 D、13或18

查看试题解析
7. 抛物线y₁=ax²+bx+c与直线y₂=mx+n的图象如图所示，下列判断中：①abc＜0；②a+b+c＞0；③5a-c=0；④当x＜ $\frac{1}{2}$ 或x＞6时，y₁＞y₂ ，其中正确的个数有（）

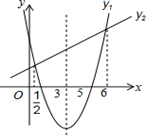A、1 B、2 C、3 D、4

查看试题解析
8. 将一副三角尺（在 $R t Δ A B C$ 中， ∠ACB=90°， ∠B=60° ，在 $R t Δ E D F$ 中， ∠EDF=90°， ∠E=45° ）如图摆放，点 $D$ 为 $A B$ 的中点， $D E$ 交 $A C$ 于点 $P$ ， $D F$ 经过点 $C$ ，将 $Δ E D F$ 绕点 $D$ 顺时针方向旋转 $α$ （ 0°＜α＜60°）， $D E^{'}$ 交 $A C$ 于点 $M$ ， $D F^{'}$ 交 $B C$ 于点 $N$ ，则 $\frac{P M}{C N}$ 的值为（）

A、 $\sqrt{3}$ B、 $\frac{\sqrt{3}}{2}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{1}{2}$

查看试题解析

二、填空题

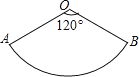
9. 把多项式8a³﹣2a分解因式的结果是.

查看试题解析
10. 若关于 $x$ 的一元二次方程 $m x^{2} - 2 x - 1 = 0$ 无实数根，则一次函数 $y = m x + m$ 的图象不经过第象限.

查看试题解析
11. 一个袋子中装有3个红球和2个黄球，这些球的形状、大小.质地完全相同，在看不到球的条件下，随机从袋子里同时摸出2个球，其中2个球的颜色相同的概率是.

查看试题解析
12.
如图所示的扇形是一个圆锥的侧面展开图，若∠AOB=120°，弧AB的长为12πcm，则该圆锥的侧面积为 cm² ．

查看试题解析
13. 在△ABC中，AB=13cm，AC=20cm，BC边上的高为12cm，则△ABC的面积为 cm² ．

查看试题解析
14. 如图，在扇形CAB中，CD⊥AB，垂足为D，⊙E是△ACD的内切圆，连接AE，BE，则∠AEB的度数为.

查看试题解析
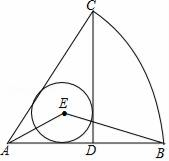15. 如图，OA＝AB，∠OAB＝90°，双曲线y＝ $\frac{k}{x}$ 经过点A，双曲线y＝﹣ $\frac{k}{x}$ 经过点B，已知点A的纵坐标为﹣2，则点B的坐标为.

查看试题解析
16. 如图放置的 $Δ O A B_{1} ， Δ B_{1} A_{1} B_{2} ， Δ B_{2} A_{2} B_{3} ， \dots$ 都是边长为1的等边三角形，点 $A$ 在 $x$ 轴上，点 $O ， B_{1} ， B_{2} ， B_{3} ， \dots$ 都在直线 $l$ 上，则点 $A_{2019}$ 的坐标是.

查看试题解析

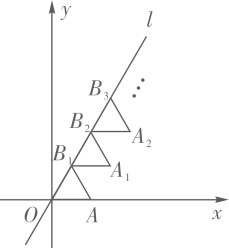
三、解答题

17. 计算： $2 \cos 30^{0} - | \sqrt{3} - 1 | + {(\frac{1}{2})}^{- 1}$ .

查看试题解析
18. 先化简再求值： $(\frac{3}{x - 1} - x - 1) \div \frac{x - 2}{x^{2} - 2 x + 1}$ ，其中x是方程x²=2x的根．

查看试题解析
19.
如图，在平行四边形ABCD中，AB＜BC．

(1)、利用尺规作图，在BC边上确定点E，使点E到边AB，AD的距离相等（不写作法，保留作图痕迹）；

(2)、若BC=8，CD=5，则CE= ．

查看试题解析
20. 中华文明，源远流长；中华汉字，寓意深广．为了传承中华民族优秀传统文化，我市某中学举行“汉字听写”比赛，赛后整理参赛学生的成绩，将学生的成绩分为A ， B ， C ， D四个等级，并将结果绘制成如图所示的条形统计图和扇形统计图，但均不完整．

请你根据统计图解答下列问题：

(1)、参加比赛的学生共有名；

(2)、在扇形统计图中，m的值为，表示“D等级”的扇形的圆心角为度；

(3)、组委会决定从本次比赛获得A等级的学生中，选出2名去参加全市中学生“汉字听写”大赛．已知A等级学生中男生有1名，请用列表法或画树状图法求出所选2名学生恰好是一名男生和一名女生的概率．

查看试题解析
21.
如图，在一次军事演习中，蓝方在一条东西走向的公路上的A处朝正南方向撤退，红方在公路上的B处沿南偏西60°方向前进实施拦截，红方行驶1000米到达C处后，因前方无法通行，红方决定调整方向，再朝南偏西45°方向前进了相同的距离，刚好在D处成功拦截蓝方，求拦截点D处到公路的距离（结果不取近似值）．

查看试题解析
22. 如图，一次函数 $y = x + b$ 与反比例函数 $y = \frac{k}{x}$ 的图象交于 $A (m ， 3) ， B (- 3 ， n)$ 两点，过点 $B$ 作 $B C ⊥ x$ 轴，垂足为点 $C$ ，且 $S_{A B C} = 5$ 。

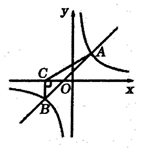(1)、求一次函数与反比例函数的表达式；

(2)、根据所给条件，请直接写出不等式 $x + b \leq \frac{k}{x}$ 的解集；

(3)、若 $P (p ， y_{1}) ， Q (- 2 ， y_{2})$ 是反比例函数 $y = \frac{k}{x}$ 图象上的两点，且 $y_{1} \geq y_{2}$ ，求实数 $P$ 的取值范围。

查看试题解析
23. 已知：如图，在△ABC中，AB=AC，点P是底边BC上一点且满足PA=PB，⊙O是△PAB的外接圆，过点P作PD∥AB交AC于点D.

(1)、求证：PD是⊙O的切线；

(2)、若BC=8，tan∠ABC= $\frac{\sqrt{2}}{2}$ ，求⊙O的半径.

查看试题解析
24. 一租赁公司拥有某种型号的汽车10辆，公司在经营中发现每辆汽车每天的租赁价为120元时可全部出租，租赁价每涨3元就少出租1辆，公司决定采取涨价措施.

(1)、填空：每天租出的汽车数 $y ($ 辆 $)$ 与每辆汽车的租赁价 $x ($ 元 $)$ 之间的关系式为.

(2)、已知租出的汽车每辆每天需要维护费30元，求租出汽车每天的实际收入 $w ($ 元 $)$ 与每辆汽车的租赁价 $x ($ 元 $)$ 之间的关系式； $($ 租出汽车每天的实际收入 $=$ 租出收入 $-$ 租出汽车维护费 $)$

(3)、若未租出的汽车每辆每天需要维护费12元，则每辆汽车每天的租赁价 $x ($ 元 $)$ 定为多少元时，才能使公司获得日收益 $z ($ 元 $)$ 最大？并求出公司的最大日收益.

查看试题解析