江苏省盐都区2019届九年级下学期数学第一次月考试卷
试卷更新日期:2020-03-10 类型:月考试卷
一、单选题
-
1. 一元二次方程(x﹣2)2=9的两个根分别是( )A、x1=1,x2=﹣5 B、x1=﹣1,x2=﹣5 C、x1=1,x2=5 D、x1=﹣1,x2=52. ⊙O的半径为4,点P到圆心O的距离为d,如果点P在圆内,则d( )A、d<4 B、d=4 C、d>4 D、0≤d<43. 若x1和x2为一元二次方程x2+2x﹣1=0的两个根.则x12x2+x1x22值为( )A、4 B、2 C、4 D、34. 若△ABC∽△DEF,且△ABC与△DEF的面积比是 ,则△ABC与△DEF对应中线的比为( )A、 B、 C、 D、5. 二次函数 的对称轴是A、直线 B、直线 C、y轴 D、x轴6. 如图,在△ABC中,AB=8,AC=6,∠BAC=30°,将△ABC绕点A逆时针旋转60°得到△AB1C1 , 连接BC1 , 则BC1的长为( )
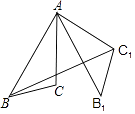 A、6 B、8 C、10 D、127. 若二次函数y=kx2﹣4x+1的图象与x轴有交点,则k的取值范围是( )A、k≤4 B、k≥4 C、k>4且k≠0 D、k≤4且k≠08. 如图,AB是⊙O的直径,C、D是⊙O上两点,∠AOC=130°,则∠D等于( )
A、6 B、8 C、10 D、127. 若二次函数y=kx2﹣4x+1的图象与x轴有交点,则k的取值范围是( )A、k≤4 B、k≥4 C、k>4且k≠0 D、k≤4且k≠08. 如图,AB是⊙O的直径,C、D是⊙O上两点,∠AOC=130°,则∠D等于( ) A、65° B、35° C、25° D、15°
A、65° B、35° C、25° D、15°二、填空题
-
9. 一组数据﹣1,3,7,4的极差是.10. 若一三角形的三边长分别为5、12、13,则此三角形的内切圆半径为.
 11. 把抛物线y=﹣(x﹣2)2﹣2先向左平移1个单位,再向下平移1个单位,得到的抛物线的解析式为。12. 如图,AB是⊙O的直径,弦CD⊥AB于点E,
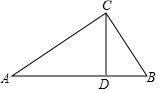
11. 把抛物线y=﹣(x﹣2)2﹣2先向左平移1个单位,再向下平移1个单位,得到的抛物线的解析式为。12. 如图,AB是⊙O的直径,弦CD⊥AB于点E, (1)、若CD=16,BE=4,则⊙O的半径为;(2)、点M在⊙O上,MD恰好经过圆心O,连接MB,若∠M=∠D,则∠D的度数为.13. 如图,用圆心角为120°,半径为6cm的扇形纸片卷成一个圆锥形无底纸帽,则这个纸帽的高是cm .
(1)、若CD=16,BE=4,则⊙O的半径为;(2)、点M在⊙O上,MD恰好经过圆心O,连接MB,若∠M=∠D,则∠D的度数为.13. 如图,用圆心角为120°,半径为6cm的扇形纸片卷成一个圆锥形无底纸帽,则这个纸帽的高是cm .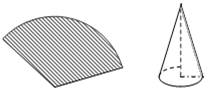 14. 一个正n边形的中心角等于18°,那么n=.15. 请你写出一个正方形具有而平行四边形不一定具有的特征: .16. 已知:如图,∠MON=90°,四边形ABCD为矩形,A、B两点分别在射线ON、OM上,AD=2,AB=4,A、B两点在ON、OM上滑动时,C、D点随之运动,则线段OD的最大值为.
14. 一个正n边形的中心角等于18°,那么n=.15. 请你写出一个正方形具有而平行四边形不一定具有的特征: .16. 已知:如图,∠MON=90°,四边形ABCD为矩形,A、B两点分别在射线ON、OM上,AD=2,AB=4,A、B两点在ON、OM上滑动时,C、D点随之运动,则线段OD的最大值为.
三、解答题
-
17. 解方程:(1)、x2﹣3x=0(2)、2x2﹣4x﹣5=0(3)、x(x﹣1)=0(4)、(x﹣1)2=3x﹣318. 计算:﹣24﹣ +|1﹣4sin60°|+(2015π)0.19. 关于x的一元二次方程x2+2x+2k﹣4=0有两个不相等的实数根.(1)、求k的取值范围;(2)、若方程的一个根为2,求另一个根.20. 为了让同学们了解自己的体育水平,初二1班的体育刘老师对全班45名学生进行了一次体育模拟测试(得分均为整数),成绩满分为10分,1班的体育委员根据这次测试成绩,制作了统计图和分析表如下:

初二1班体育模拟测试成绩分析表
平均分
方差
中位数
众数
男生
2
8
7
女生
7.92
1.99
8
根据以上信息,解答下列问题:
(1)、这个班共有男生人,共有女生人;(2)、补全初二1班体育模拟测试成绩分析表.21. 今年某市为创评“全国文明城市”称号,周末团市委组织志愿者进行宣传活动.班主任梁老师决定从4名女班干部(小悦、小惠、小艳和小倩)中通过抽签的方式确定2名女生去参加.抽签规则:将4名女班干部姓名分别写在4张完全相同的卡片正面,把四张卡片背面朝上,洗匀后放在桌面上,梁老师先从中随机抽取一张卡片,记下姓名,再从剩余的3张卡片中随机抽取第二张,记下姓名.
(1)、该班男生“小刚被抽中”是事件,“小悦被抽中”是事件(填“不可能”或“必然”或“随机”);第一次抽取卡片“小悦被抽中”的概率为;(2)、试用画树状图或列表的方法表示这次抽签所有可能的结果,并求出“小惠被抽中”的概率.22. 如图,已知:二次函数y=x2+bx+c 的图象与x轴交于A,B两点,其中A点坐标为(-3,0),与 y 轴交于点 C(0,-3)在抛物线上. (1)、求抛物线的表达式;(2)、抛物线的对称轴上有一动点 P,求出当 PB+PC 最小时点 P的坐标;(3)、若抛物线上有一动点Q,使△ABQ的面积为6,求Q点坐标.23. 如图1,2分别是某款篮球架的实物图与示意图,已知AB⊥BC于点B,底座BC的长为1米,底座BC与支架AC所成的角∠ACB=60°,点H在支架AF上,篮板底部支架EH∥BC,EF⊥EH于点E,已知AH长 米,HF长 米,HE长1米.
(1)、求抛物线的表达式;(2)、抛物线的对称轴上有一动点 P,求出当 PB+PC 最小时点 P的坐标;(3)、若抛物线上有一动点Q,使△ABQ的面积为6,求Q点坐标.23. 如图1,2分别是某款篮球架的实物图与示意图,已知AB⊥BC于点B,底座BC的长为1米,底座BC与支架AC所成的角∠ACB=60°,点H在支架AF上,篮板底部支架EH∥BC,EF⊥EH于点E,已知AH长 米,HF长 米,HE长1米. (1)、求篮板底部支架HE与支架AF所成的角∠FHE的度数.(2)、求篮板底部点E到地面的距离.(结果保留根号)24. 某商店销售一种成本为20元的商品,经调研,当该商品每件售价为30元时,每天可销售200件:当每件的售价每增加1元,每天的销量将减少5件.(1)、求销量 件 与售价 元 之间的函数表达式;(2)、如果每天的销量不低于150件,那么,当售价为多少元时,每天获取的利润最大,最大利润是多少?(3)、该商店老板热心公益事业,决定从每天的销售利润中捐出100元给希望工程,为保证捐款后每天剩余利润不低于2900元,请直接写出该商品售价的范围.25. 如图,点C是以AB为直径的⊙O上一点,CP与AB的延长线相交于点P,已知AB=2BP,AC= BP.
(1)、求篮板底部支架HE与支架AF所成的角∠FHE的度数.(2)、求篮板底部点E到地面的距离.(结果保留根号)24. 某商店销售一种成本为20元的商品,经调研,当该商品每件售价为30元时,每天可销售200件:当每件的售价每增加1元,每天的销量将减少5件.(1)、求销量 件 与售价 元 之间的函数表达式;(2)、如果每天的销量不低于150件,那么,当售价为多少元时,每天获取的利润最大,最大利润是多少?(3)、该商店老板热心公益事业,决定从每天的销售利润中捐出100元给希望工程,为保证捐款后每天剩余利润不低于2900元,请直接写出该商品售价的范围.25. 如图,点C是以AB为直径的⊙O上一点,CP与AB的延长线相交于点P,已知AB=2BP,AC= BP. (1)、求证:PC与⊙O相切;(2)、若⊙O的半径为3,求阴影部分弓形的面积.26. 在矩形ABCD中,AB=4,AD=8.
(1)、求证:PC与⊙O相切;(2)、若⊙O的半径为3,求阴影部分弓形的面积.26. 在矩形ABCD中,AB=4,AD=8. (1)、如图①若E从B到C运动,F从D到A运动且BE=2DF,
(1)、如图①若E从B到C运动,F从D到A运动且BE=2DF,( i)当DF为何值时四边形ECDF是矩形.
( ii)当DF为何值时EF=2 .
(2)、如图②E在BC上,BE=3,F在CD上,将△ECF沿EF折叠,当C点恰好落在AD边上的G处时,求折痕EF的长.27. 如图,在平面直角坐标系中,直线y= +2分别交x轴、y轴于点A、B,抛物线y=﹣x2+bx+c经过点A、B.点P是x轴上一个动点,过点P作垂直于x轴的直线分别交抛物线和直线AB于点E和点F.设点P的横坐标为m. (1)、点A的坐标为 .(2)、求这条抛物线所对应的函数表达式.(3)、点P在线段OA上时,若以B、E、F为顶点的三角形与△FPA相似,求m的值.(4)、若E、F、P三个点中恰有一点是其它两点所连线段的中点(三点重合除外),称E、F、P三点为“共谐点”.直接写出E、F、P三点成为“共谐点”时m的值.
(1)、点A的坐标为 .(2)、求这条抛物线所对应的函数表达式.(3)、点P在线段OA上时,若以B、E、F为顶点的三角形与△FPA相似,求m的值.(4)、若E、F、P三个点中恰有一点是其它两点所连线段的中点(三点重合除外),称E、F、P三点为“共谐点”.直接写出E、F、P三点成为“共谐点”时m的值.