江苏省兴化市顾庄学区2019届九年级下学期数学第一次月考试卷
试卷更新日期:2020-03-10 类型:月考试卷
一、单选题
-
1. 抛物线 与 轴的交点坐标为( )A、(3 ,0) B、(0 ,3) C、(0, ) D、( ,0)2. 在Rt△ABC中,∠C=90°,如果AC=4,BC=3,那么∠A的正切值为( )A、 B、 C、 D、3. 有15位学生参加学校组织的“爱我中华”演讲比赛,比赛结束后根据每位学生的最后得分计算出平均数、中位数、众数、方差.如果修改规则:先去掉一个最高分,去掉一个最低分,再进行统计,则上述四个统计量中,一定不会发生变化的是( )A、平均数 B、中位数 C、众数 D、方差4. 在一个不透明的盒子里有3个红球和若干个白球,这些球除颜色外其余完全相同,摇匀后随机摸出一个,摸到红球的概率是 ,则白球的个数是( )A、3 B、4 C、6 D、95. 如图,∠APD=90°,AP=PB=BC=CD,则下列结论成立的是( )
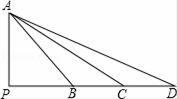 A、△PAB∽△PCA B、△ABC∽△DBA C、△PAB∽△PDA D、△ABC∽△DCA6. 如图,分别过点Pi(i,0)(i=1、2、…、n)作x轴的垂线,交 的图象于点Ai , 交直线 于点Bi.则 + 的值为( )
A、△PAB∽△PCA B、△ABC∽△DBA C、△PAB∽△PDA D、△ABC∽△DCA6. 如图,分别过点Pi(i,0)(i=1、2、…、n)作x轴的垂线,交 的图象于点Ai , 交直线 于点Bi.则 + 的值为( )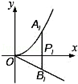 A、 B、2 C、 D、
A、 B、2 C、 D、二、填空题
-
7. 小明沿坡比为1︰ 的山坡向上走了100米.那么他升高了米.8. 如图,四边形ABCD内接于⊙O,AB为⊙O的直径,C为弧BD的中点,若∠DAB=40°,则∠ADC=.
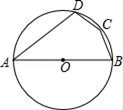 9. 某地区2017年投入教育经费2 500万元,2019年计划投入教育经费3 025万元,则2017年至2019年,该地区投入教育经费的年平均增长率为.10. 若一个扇形的半径是18cm,且它的弧长是12πcm,则此扇形的圆心角等于°.11. 已知一组数据6,6,5,x,1,请你给正整数x一个值 , 使这组数据的众数为6,中位数为5.12. 小丽同学今年在六次数学考试中的成绩分别是:117,118,120,116,118,119,则她这六次考试成绩的方差是.13. 随着北京申办冬奥会的成功,愈来愈多的同学开始关注我国的冰雪体育项目. 小健从新闻中了解到:在2018年平昌冬奥会的短道速滑男子500米决赛中,中国选手武大靖以39秒584的成绩打破世界纪录,收获中国男子短道速滑队在冬奥会上的首枚金牌. 同年11月12日,武大靖又以39秒505的成绩再破世界纪录. 于是小健对同学们说:“2022年北京冬奥会上武大靖再获金牌的可能性大小是 .”你认为小健的说法(填“合理”或“不合理”),理由是.14. 如图,双曲线y= 与抛物线y=ax2+bx+c交于点A(x1 , y1),B(x2 , y2),C(x3 , y3),由图象可得不等式组0< +bx+c的解集为.
9. 某地区2017年投入教育经费2 500万元,2019年计划投入教育经费3 025万元,则2017年至2019年,该地区投入教育经费的年平均增长率为.10. 若一个扇形的半径是18cm,且它的弧长是12πcm,则此扇形的圆心角等于°.11. 已知一组数据6,6,5,x,1,请你给正整数x一个值 , 使这组数据的众数为6,中位数为5.12. 小丽同学今年在六次数学考试中的成绩分别是:117,118,120,116,118,119,则她这六次考试成绩的方差是.13. 随着北京申办冬奥会的成功,愈来愈多的同学开始关注我国的冰雪体育项目. 小健从新闻中了解到:在2018年平昌冬奥会的短道速滑男子500米决赛中,中国选手武大靖以39秒584的成绩打破世界纪录,收获中国男子短道速滑队在冬奥会上的首枚金牌. 同年11月12日,武大靖又以39秒505的成绩再破世界纪录. 于是小健对同学们说:“2022年北京冬奥会上武大靖再获金牌的可能性大小是 .”你认为小健的说法(填“合理”或“不合理”),理由是.14. 如图,双曲线y= 与抛物线y=ax2+bx+c交于点A(x1 , y1),B(x2 , y2),C(x3 , y3),由图象可得不等式组0< +bx+c的解集为.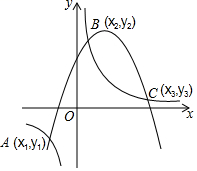 15. 如图,点G为△ABC的重心,连接AG、BG并延长,分别交BC、AC于点D、E,过点E作EF∥BC交AD于点F,那么AF:AG=.
15. 如图,点G为△ABC的重心,连接AG、BG并延长,分别交BC、AC于点D、E,过点E作EF∥BC交AD于点F,那么AF:AG=.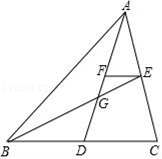 16. 如图,正方形ABCD的对角线相交于点O,正方形OEFG的一边OG经过点D,且D是OG的中点,OG= AB,若正方形ABCD固定,将正方形OEFG绕O点逆时针旋转α角,(0°<α<360°)得到正方形OE′F′G′,当α=度时,∠OAG′=90°.
16. 如图,正方形ABCD的对角线相交于点O,正方形OEFG的一边OG经过点D,且D是OG的中点,OG= AB,若正方形ABCD固定,将正方形OEFG绕O点逆时针旋转α角,(0°<α<360°)得到正方形OE′F′G′,当α=度时,∠OAG′=90°.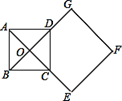
三、解答题
-
17.(1)、计算:2cos60°+4sin60°•tan30°﹣6cos245°.(2)、已知:线段a、b、c,且 .a+b+c=27,求a﹣b+c的值.18. 已知抛物线(1)、请用配方法求出顶点的坐标;(2)、如果该抛物线沿 轴向左平移 个单位后经过原点,求 的值.19. 小明周末要乘坐公交车到植物园游玩,从地图上查找路线发现,几条线路都需要换乘一次.在出发站点可选择空调车A、空调车B、普通车a,换乘站点可选择空调车C,普通车b、普通车c,且均在同一站点换乘.空调车投币2元,普通车投币1元.(1)、求小明在出发站点乘坐空调车的概率;(2)、求小明到达植物园恰好花费3元公交费的概率.20. 某校课程中心为了了解学生对开设的3D打印、木工制作、机器人和电脑编程四门课程的喜爱程度,随机调查了部分学生,每人只能选一项最喜爱的课程.图①是四门课程最喜爱人数的扇形统计图,图②是四门课程男、女生最喜爱人数的条形统计图.
 (1)、求图①中 的值,补全图②中的条形统计图,标上相应的人数;(2)、若该校共有1800名学生,则该校最喜爱3D打印课程的学生约有多少人?21. 如图,已知直线AC与⊙O相交于点C,直线AO与⊙O相交于D,B两点.已知∠ACD=∠B.
(1)、求图①中 的值,补全图②中的条形统计图,标上相应的人数;(2)、若该校共有1800名学生,则该校最喜爱3D打印课程的学生约有多少人?21. 如图,已知直线AC与⊙O相交于点C,直线AO与⊙O相交于D,B两点.已知∠ACD=∠B.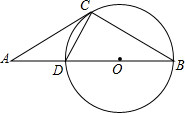 (1)、求证:AC是⊙O的切线;(2)、若AC=6,AD=4,求⊙O的半径;22. 如图,一块材料的形状是锐角三角形ABC,边BC长120mm,高AD为80mm,把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1)、求证:AC是⊙O的切线;(2)、若AC=6,AD=4,求⊙O的半径;22. 如图,一块材料的形状是锐角三角形ABC,边BC长120mm,高AD为80mm,把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.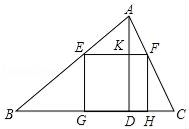 (1)、图中与△ABC相似的三角形是哪一个,说明理由;(2)、这个正方形零件的边长为多少?23. 如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡AF上的D处测得大树顶端B的仰角是30°,在地面上A处测得大树顶端B的仰角是45°.若坡角∠FAE=30°,AD=6m,求大树的高度.(结果保留整数,参考数据: ≈1.73)
(1)、图中与△ABC相似的三角形是哪一个,说明理由;(2)、这个正方形零件的边长为多少?23. 如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡AF上的D处测得大树顶端B的仰角是30°,在地面上A处测得大树顶端B的仰角是45°.若坡角∠FAE=30°,AD=6m,求大树的高度.(结果保留整数,参考数据: ≈1.73) 24. 如图,在平面直角坐标系 中,抛物线 与 轴相交于原点 和点 ,点 在抛物线上.
24. 如图,在平面直角坐标系 中,抛物线 与 轴相交于原点 和点 ,点 在抛物线上. (1)、求抛物线的表达式,并写出它的对称轴;(2)、求 的值.25. 如图,在矩形ABCD中,AC为对角线,点P为BC边上一动点,连接AP,过点B作BQ⊥AP,垂足为Q,连接CQ.
(1)、求抛物线的表达式,并写出它的对称轴;(2)、求 的值.25. 如图,在矩形ABCD中,AC为对角线,点P为BC边上一动点,连接AP,过点B作BQ⊥AP,垂足为Q,连接CQ. (1)、证明:△ABP∽△BQP;(2)、当点P为BC的中点时,若∠BAC=37°,求∠CQP的度数;(3)、当点P运动到与点C重合时,延长BQ交CD于点F,若AQ=AD,则 等于多少.26. 在平面直角坐标系中,已知二次函数y=ax2﹣2ax﹣3a(a>0)图象与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,顶点为D.(1)、求点A,B的坐标;(2)、若M为对称轴与x轴交点,且DM=2AM.
(1)、证明:△ABP∽△BQP;(2)、当点P为BC的中点时,若∠BAC=37°,求∠CQP的度数;(3)、当点P运动到与点C重合时,延长BQ交CD于点F,若AQ=AD,则 等于多少.26. 在平面直角坐标系中,已知二次函数y=ax2﹣2ax﹣3a(a>0)图象与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,顶点为D.(1)、求点A,B的坐标;(2)、若M为对称轴与x轴交点,且DM=2AM.①求二次函数解析式;
②当t﹣2≤x≤t时,二次函数有最大值5,求t值;
③若直线x=4与此抛物线交于点E,将抛物线在C,E之间的部分记为图象记为图象P(含C,E两点),将图象P沿直线x=4翻折,得到图象Q,又过点(10,﹣4)的直线y=kx+b与图象P,图象Q都相交,且只有两个交点,求b的取值范围.