江苏省东台市第三联盟2019届九年级下学期数学第一次月考试卷

试卷更新日期：2020-03-10 类型：月考试卷

进入出卷网下载

一、单选题

1. 计算 $1 - 2 =$ （）

A、0 B、1 C、－1 D、－2

查看试题解析
2. 下列计算正确的是（）

A、 $2 a + 3 b = 5 a b$ B、 ${(a - b)}^{2} = a^{2} - b^{2}$ C、 $a^{6} \div a^{3} = a^{2}$ D、 ${(a b)}^{2} = a^{2} b^{2}$

查看试题解析
3.
如图，BC= $\frac{1}{2}$ AB，D为AC的中点，DC=3cm，则AB的长是（　　）

A、3cm B、4cm C、5cm D、6cm

查看试题解析
4. 同学们都玩过跷跷板的游戏，如图，是一个跷跷板的示意图，立柱 $O C$ 与地面垂直， $O A = O B$ ，当跷跷板的一头着地时， $∠ O A C = 25^{0}$ ，则当跷跷板的另一头 $B$ 着地时 $∠ A O A'$ 等于（）

A、 $25^{0}$ B、 $50^{0}$ C、 $60^{0}$ D、 $130^{0}$

查看试题解析
5.
如图，在平面直角坐标系中，以O为圆心，适当长为半径画弧，交x轴于点M，交y轴于点N，再分别以点M、N为圆心，大于 $\frac{1}{2}$ MN的长为半径画弧，两弧在第二象限交于点P．若点P的坐标为（2a，b+1），则a与b的数量关系为（　　）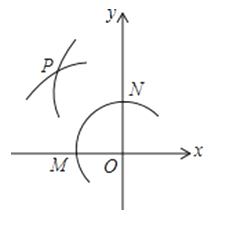

A、a=b B、2a+b=﹣1 C、2a﹣b=1 D、2a+b=1

查看试题解析
6. 下列图案是一副扑克牌的四种花色，其中既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
7. 如图，一次函数 $y = a x + b$ 与 $x$ 轴， $y$ 轴交于 $A ， B$ 两点，与反比例函数 $y = \frac{k}{x}$ 相交于 $C ， D$ 两点，分别过 $C ， D$ 两点作 $y$ 轴， $x$ 轴的垂线，垂足为 $E ， F$ ，连接 $C F ， D E ， E F$ ，有下列四个结论：① $Δ C E F$ 与 $Δ D E F$ 的面积相等；② $Δ A O B$ ∽ $Δ F O E$ ；③ $Δ D C E ≅ Δ C D F$ ；④ $A C = B D$ ，其中正确的结论个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

8. 我国是一个严重缺水的国家，大家应加倍珍惜水资源，节约用水，据测试，拧不紧的水龙头每秒钟会滴下 2 滴水，每滴水约 0.05 毫升.小明同学在洗手后，没有把水龙头拧紧，当小明离开 4 小时后水龙头滴了约毫升水（用科学记数法表示）.

查看试题解析
9. 若 $a^{2} - b^{2} = 8$ ， $b - a = 3$ ，则 $a + b =$ .

查看试题解析
10. 若关于 $x$ 方程 $k x^{2} - 6 x + 1 = 0$ 有两个实数根，则 $k$ 的取值范围是.

查看试题解析
11. 如图，在 $Δ A B C$ 中， $A B = A C$ ， $∠ B = 50^{0}$ ，⊙ $A$ 与 $B C$ 相切于点 $D$ ，与 $A B$ 相交于点 $E$ ，则 $∠ A E D =$ °.

查看试题解析
12.
如图，△ABC中，CD⊥AB于D，E是AC的中点．若AD=6，DE=5，则CD的长等于

查看试题解析
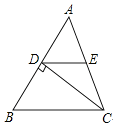13. 如图，在 8×4 的矩形网格中，每个小正方形的边长都是 1，若 $Δ A B C$ 的三个顶点在图中相应的格点上，则 $\tan ∠ A C B$ 的值为

查看试题解析
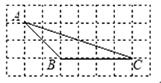14. 甲、乙、丙三台机床生产直径为 $60 m m$ 的螺丝，为了检验产品质量，从三台机床生产的螺丝中各抽取了 20 个，测量其直径，进行数据处理后，发现三组数据的平均数都是 $60 m m$ ，它们的方差依次为 $S_{甲}^{2} = 0.612$ ， $S_{乙}^{2} = 0.058$ ， $S_{丙}^{2} = 0.149$ ，根据以上提供的信息，你认为生产螺丝的质量最好的是机床.

查看试题解析
15. 如图，矩形纸片 $A B C D$ 中， $A B = 6 c m$ ， $B C = 10 c m$ ，点 $E$ 在 $A B$ 边上，将 $Δ E B C$ 沿 $E C$ 所在直线折叠，使点 $B$ 落在 $A D$ 边上的点 $B'$ 处，则 $A E$ 的长为 $c m$ .

查看试题解析
16. 五羊自行车厂组织 78 位劳动模范参观科普展览，为了节省经费，决定让其中 10 位劳模兼任司机.厂里有 2 种汽车：大车需 1 名司机，可坐 11 位乘客；小车需 1 名司机，可坐 4 名乘客.大车每辆出车费用为 150元，小车每辆出车费用为 70 元.现备有大车 7 辆，小车 8 辆.为使费用最省，应安排开出大车辆.

查看试题解析
17.
如图，直线l₁⊥x轴于点A（2，0），点B是直线l₁上的动点．直线l₂：y=x+1交l₁于点C，过点B作直线l₃垂直于l₂ ，垂足为D，过点O，B的直线l₄交l₂于点E，当直线l₁ ， l₂ ， l₃能围成三角形时，设该三角形面积为S₁ ，当直线l₂ ， l₃ ， l₄能围成三角形时，设该三角形面积为S₂ ．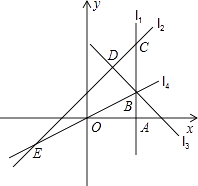

(1)、若点B在线段AC上，且S₁=S₂ ，则B点坐标为；

(2)、若点B在直线l₁上，且S₂= $\sqrt{3}$ S₁ ，则∠BOA的度数为．

查看试题解析

三、解答题

18. 计算： $2^{- 1} - 3 \tan 30^{0} + {(1 - \sqrt{2})}^{0} + \sqrt{12}$

查看试题解析
19. 先化简，再求值： $\frac{1}{x + 2} - \frac{x^{2} - 4 x + 4}{x^{2} - x} \div (x + 1 - \frac{3}{x - 1})$ ，其中 $x$ 满足 $x^{2} + 2 x - 4 = 0$ .

查看试题解析
20. 如图，把一个转盘分成四等份，依次标上数字：1，2，3，4，若连续自由转动转盘二次，指针指向的数字分别记作a，b，把a，b作为点A的横、纵坐标.

(1)、用列表法或树状图表示出A（a，b）所有可能出现的结果；

(2)、求点A（a，b）在函数 $y = x$ 的图象上的概率.

查看试题解析
21. 某中学开展“绿化家乡、植树造林”活动，为了解全校植树情况，对该校甲、乙、丙、丁四个班级植树的棵树和所占百分比情况进行了调查，将收集的数据整理并绘制成图 1 和图 2 两幅不完整的统计图，请根据图中的信息，完成下列问题：

(1)、这四个班共植树棵；

(2)、请补全两幅统计图；

(3)、若四个班级植树的平均成活率是 95%，全校共植树 2000 棵，请你估计全校种植的树中成活的树大约有多少棵？

查看试题解析
22. 如图所示，在矩形 $A B C D$ 中， $E$ 是 $B C$ 边上的点， $A E = B C$ ， $D F ⊥ A E$ ，垂足为 $F$ ，连接 $D E$ .

(1)、求证： $A B = D F$ ；

(2)、若 $A D = 10$ ， $A B = 6$ ，求 $\tan ∠ E D F$ 的值.

查看试题解析
23. 如图，在平面直角坐标系中，直线 $y_{1} = 2 x - 2$ 与反比例函数 $y_{2} = \frac{k}{x}$ 的图像在第一象限交于点 $A (2 ， n)$ ，在第三象限交于点 $B$ ，过 $B$ 作 $B D ⊥ x$ 轴于 $D$ ，连接 $A D$ .

(1)、求反比例函数的解析式；

(2)、求 $Δ A B D$ 的面积 $S_{Δ A B D}$ ；

(3)、根据图象直接写出 $y_{1} > y_{2}$ 时自变量 $x$ 的取值范围.

查看试题解析

24. 为了节约资源，科学指导居民改善居住条件，小王向房管部门提出了一个购买商品房的政策性方案.

人均住房面积（平方米）	单价（万元/平方米）
不超过30（平方米）	0.3
超过30平方米不超过m（平方米）部分（45≤m≤60）	0.5
超过m平方米部分	0.7

根据这个购房方案：

(1)、若某三口之家欲购买120平方米的商品房，求其应缴纳的房款；

(2)、设该家庭购买商品房的人均面积为x平方米，缴纳房款y万元，请求出y关于x的函数关系式；

(3)、若该家庭购买商品房的人均面积为50平方米，缴纳房款为y万元，且57＜y≤60 时，求m的取值范围.

查看试题解析

25. 如图，已知 $Δ A B C$ 为直角三角形， $∠ A C B = 90^{0}$ ， $A C = B C$ ，点 $A ， C$ 在 $x$ 轴上，点 $B$ 坐标为 $(3 ， m) (m > 0)$ ，线段 $A B$ 与 $y$ 轴相交于点 $D$ ，以 $P (1 ， 0)$ 为顶点的抛物线过点 $B ， D$ .

(1)、求点 $A$ 的坐标（用 $m$ 表示）；

(2)、求抛物线的解析式；

(3)、设点 $Q$ 为抛物线上点 $P$ 至点 $B$ 之间的一动点，连接 $P Q$ 并延长交 $B C$ 于点 $E$ ，连接 $B Q$ 并延长交 $A C$ 于点 $F$ ，试证明： $F C (A C + E C)$ 为定值.

查看试题解析
26. 如图，矩形ABCD的边AB=3cm，AD=4cm，点E从点A出发，沿射线AD移动，以CE为直径作圆O，点F为圆O与射线BD的公共点，连接EF、CF，过点E作EG⊥EF，EG与圆O相交于点G，连接CG．

(1)、试说明四边形EFCG是矩形；

(2)、当圆O与射线BD相切时，点E停止移动，在点E移动的过程中，
①矩形EFCG的面积是否存在最大值或最小值？若存在，求出这个最大值或最小值；若不存在，说明理由；
②求点G移动路线的长．

查看试题解析