江苏南通市崇川区2019届九年级下学期数学第一次月考试卷
试卷更新日期：2020-03-10 类型：月考试卷
一、单选题
-
1. 若反比例函数y＝ (k≠0)的图象经过点P(2，﹣3)，则该函数的图象不经过的点是（ ）A、(3，﹣2) B、(1，﹣6) C、(﹣1，6) D、(﹣1，﹣6)2. 小王抛一枚质地均匀的硬币，连续抛4次，硬币均正面朝上落地，如果他再抛第5次，那么硬币正面朝上的概率为（ ）A、1 B、 C、 D、3. 点P1(－1，y1)，P2(3，y2)，P3(5，y3)均在二次函数y=－x2＋2x＋c的图象上，则y1 ， y2 ， y3的大小关系是（ ）A、y3>y2>y1 B、y3>y1=y2 C、y1>y2>y3 D、y1=y2>y34. 如图，Rt△ABC中，∠ACB＝90°，线段BC绕点B逆时针旋转α°（0＜α＜180）得到线段BD，过点A作AE⊥射线CD于点E，则∠CAE的度数是（ ）
A、90﹣α B、α C、 D、5. 若圆锥的底面半径为6cm，母线为8cm，则圆锥的侧面积是 （ ）A、 cm2 B、 cm2 C、 cm2 D、 cm26. 反比例函数y＝ 图象经过A（1，2），B（n，﹣2）两点，则n＝（ ）A、1 B、3 C、﹣1 D、﹣37. 在⊙O中，弦AB的长为2 cm，圆心O到AB的距离为1cm，则⊙O的半径是（ ）A、2 B、3 C、 D、8. 在不透明的袋子里装有16个红球和若干个白球，这些球除颜色不同外无其它差别 每次从袋子里摸出一个球记录下颜色后再放回，经过多次重复试验，发现摸到白球的频率稳定在 ，则袋中白球有A、12个 B、20个 C、24个 D、40个9. 如图，AB是⊙O的直径，CD是⊙O的切线，切点为D ， CD与AB的延长线交于点C ， ∠A＝30°，CD＝3，则AB的值是（ ）
A、3 B、 C、6 D、10. 在同一直角坐标系中，二次函数y＝x2与反比例函数y （x＞0）的图象如图所示，若两个函数图象上有三个不同的点A（x1 ， m），B（x2 ， m），C（x3 ， m），其中m为常数，令ω＝x1+x2+x3 ， 则ω的值为（ ）
A、1 B、m C、m2 D、二、填空题
-
11. 已知正六边形的边心距为 ，则它的周长是 ．12. 若抛物线C1：y＝x2+mx+2与抛物线C2：y＝x2﹣3x+n关于y轴对称，则m+n＝.13. 如图，已知直线 a∥b∥c，直线 m，n 与直线 a，b，c 分别交于点 A，C，E，B，D，F， 若 AC＝4，CE＝6，BD＝3，则 DF 的值是.
14. 已知 的半径为4cm，点P在直线l上，且点P到圆心O的距离为4cm，则直线l与 .15. 反比例函数y＝ 的图象满足：在所在象限内，y随x的增大而减小，则n的取值范围是.16. 如图，在长方形ABCD中，AB＝4cm，BC＝8cm.E、F分别是AB、BC的中点.则E到DF的距离是cm.
17. 抛物线 经过原点，那么该抛物线在对称轴左侧的部分是的.（填“上升”或“下降”）18. 如图，A，B，C三点在正方形网格线的交点处，将△ACB绕着点A逆时针旋转得到△AC′B′，若A，C，B′三点共线，则tan∠B′CB=.
三、解答题
-
19. 已知反比例函数的图象经过点A(2，6).(1)、求这个反比例函数的解析式；(2)、这个函数的图象位于哪些象限？y随x的增大如何变化？(3)、点B(3，4)，C(5，2)，D( ， )是否在这个函数图象上？为什么？20. 如图所示，Rt△ABC中，∠C＝90°，点D、E分别在AC、AB上，BD平分∠ABC，DE⊥AB，cotA＝ ，求tan∠DBC的值.
21. 现如今，“垃圾分类”意识已深入人心，如图是生活中的四个不同的垃圾分类投放桶.其中甲投放了一袋垃圾，乙投放了两袋垃圾.
(1)、直接写出甲投放的垃圾恰好是“厨余垃圾”的概率；(2)、求乙投放的两袋垃圾不同类的概率.22. 已知△ABC在平面直角坐标系中的位置如图所示：
(1)、画出△ABC绕点A按逆时针方向旋转90°后的△A′B′C′；
(2)、在（1）的条件下，求点C旋转到点C′所经过的路线长及线段AC旋转到新位置时所划过区域的面积.
23. 如图，在四边形ABCD中，AD∥BC，AB⊥BC，点E在AB上，∠DEC＝90°.
(1)、求证：△ADE∽△BEC.(2)、若AD＝1，BC＝3，AE＝2，求AB的长.24. 如图，AB是⊙O的直径，点C在⊙O上，CE⊥AB于E，BD交CE于点F，CF＝BF，
(1)、求证：C是 的中点；(2)、若CD＝4，AC＝8，则⊙O的半径为.25. 矩形AOBC中，OB=4，OA=3.分别以OB，OA所在直线为x轴，y轴，建立如图1所示的平面直角坐标系.F是BC边上一个动点（不与B，C重合），过点F的反比例函数y= （k＞0）的图象与边AC交于点E。
(1)、当点F运动到边BC的中点时，求点E的坐标；(2)、连接EF，求∠EFC的正切值；(3)、如图2，将△CEF沿EF折叠，点C恰好落在边OB上的点G处，求此时反比例函数的解析式.26. 某农户承包荒山种植某产品种蜜柚.已知该蜜柚的成本价为8元/千克，投入市场销售时，调查市场行情，发现该蜜柚销售不会亏本，且每天销量y(千克)与销售单价x(元/千克)之间的函数关系如图所示.
(1)、求y与x的函数关系式，并写出x的取值范围；(2)、当该品种蜜柚定价为多少时，每天销售获得的利润最大？最大利润是多少？27. 已知锐角∠MBN的余弦值为 ，点C在射线BN上，BC＝25，点A在∠MBN的内部，且∠BAC＝90°，∠BCA＝∠MBN.过点A的直线DE分别交射线BM、射线BN于点D、E.点F在线段BE上（点F不与点B重合），且∠EAF＝∠MBN.
(1)、如图1，当AF⊥BN时，求EF的长；(2)、如图2，当点E在线段BC上时，设BF＝x，BD＝y，求y关于x的函数解析式并写出函数定义域；(3)、联结DF，当△ADF与△ACE相似时，请直接写出BD的长.28. 已知二次函数y=ax2+bx+c图象的对称轴为y轴，且过点(1，2)，(2，5).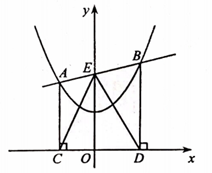
(1)、求二次函数的解析式；(2)、如图，过点E(O，2)的一次函数图象与二次函数的图象交于A，B两点（A点在B点的左侧），过点A，B分别作AC⊥x轴于点C，BD⊥x轴于点D。①当CD=3时，求该一次函数的解析式；
②分别用S1 ， S2 ， S3表示△ACE，△ECD，△EDB的面积，问是否存在实数t，使得 =tS1S3 ， 都成立？若存在，求出t的值；若不存在，说明理由。