浙江省绍兴市六校2018-2019学年七年级下学期数学3月月考试卷

试卷更新日期：2020-03-10 类型：月考试卷

进入出卷网下载

一、单选题

1. 已知 ${\begin{array}{l} x = 1 \\ y = - 1 \end{array}$ 是方程 $2 x - a y = 3$ 的一组解，那么 $a$ 的值为（）

A、1 B、3 C、-3 D、-15

查看试题解析
2. 下列各图中， $∠ 1$ 与 $∠ 2$ 是同位角的是（）

A、 B、 C、 D、

查看试题解析
3. 如图，a∥b，将一块三角板的直角顶点放在直线a上，∠1=42°，则∠2的度数为（）

A、46° B、48° C、56° D、72°

查看试题解析
4. 在① $\frac{2}{x}$ +y=1；②3x-2y=1；③5xy=1；④ $\frac{x}{2}$ +y=1四个式子中，不是二元一次方程的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 如图，已知AB∥CD，BC平分∠ABE，∠C=33°，则∠BED的度数是（）

A、16° B、33° C、49° D、66°

查看试题解析
6. 下列现象属于平移的是（）
①打气筒活塞的轮复运动，②电梯的上下运动，③钟摆的摆动，④转动的门，⑤汽车在一条笔直的马路上行走．

A、③ B、②③ C、①②④ D、①②⑤

查看试题解析
7. 如图，点E在AC的延长线上，下列条件能判断AB∥CD的是（）
①∠1=∠2；②∠3=∠4；③∠A=∠DCE； ④∠D+∠ABD=180°.

A、①③④ B、①②③ C、①②④ D、②③④

查看试题解析
8. 互联网“微商”经营已成为大众创业新途径，某微信平台上一件商品进价为200元，按标价的五折销售，仍可获利10%，设这件商品的标价为x元，根据题意列出方程（）.

A、 $0.5 x - 200 = 10 % \times 200$ B、 $0.5 x - 200 = 10 % \times 0.5 x$ C、 $200 = (1 - 10 %) \times 0.5 x$ D、 $0.5 x = (1 - 10 %) \times 200$

查看试题解析
9. 在3×3方格上做填字游戏，要求每行每列及对角线上三个方格中的数字和都等于S，又填在图中三格中的数字如图，若要能填成，则（）

A、S=24 B、S=30 C、S=31 D、S=39

查看试题解析
10. 如图在 $Δ A B C$ 中，已知 $∠ 1 + ∠ 2 = 180 °$ ， $∠ 3 = ∠ B = 72 °$ ， $⊥$ ，则 $∠ C =$ （）

A、 $32 °$ B、 $58 °$ C、 $72 °$ D、 $108 °$

查看试题解析

二、填空题

11. 将方程3x+2y=7变形成用含y的代数式表示x，得到.

查看试题解析
12. 买14支铅笔和6本练习本，共用5.4元．若铅笔每支x元，练习本每本y元，写出以x和y为未知数的方程为．

查看试题解析
13. 如图，将 $Δ A B C$ 平移到 $Δ A' B' C'$ 的位置（点 $B'$ 在 $A C$ 边上），若 $∠ B = 55 °$ ， $∠ C = 100 °$ ，则 $∠ A B' A'$ 的度数为.

查看试题解析
14. 如果关于x、y的方程组 ${\begin{array}{l} x + 2 y = 6 + k \\ 2 x - y = 9 - 2 k \end{array}$ 的解满足3x+y＝5，则k的值＝.

查看试题解析
15. 如图1是我们常用的折叠式小刀，图2中刀柄外形是一个矩形挖去一个小半圆，其中刀片的两条边缘线可看成两条平行的线段，转动刀片时会形成如图2所示的∠1与∠2，则∠1与∠2的度数和是度．

查看试题解析
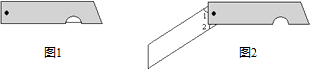16. 如果 $∠ 1$ 两边与 $∠ 2$ 的两边互相平行，且 $∠ 1 = (3 x + 20) °$ ， $∠ 2 = (8 x - 5) °$ ，则 $∠ 1$ 的度数为.

查看试题解析
17. 如图，一条公路修到湖边时，需拐弯绕湖而过，在A，B，C三处经过三次拐弯，此时道路恰好和第一次拐弯之前的道路平行（即AE∥CD），若∠A=120°，∠B=150°，则∠C的度数是．

查看试题解析
18. 如图，已知 $Δ A B C$ 的面积为16， $B C = 8$ ，现将 $Δ A B C$ 沿直线BC向右平移a个单位到 $Δ D E F$ 的位置，当 $Δ A B C$ 所扫过的面积为32时，a的值为；

查看试题解析
19. 定义一种新运算“※”，规定 $x$ ※ $y$ = $a x + b y^{2}$ ，其中 $a$ 、 $b$ 为常数，且1※2=5,2※1=3，则2※3=.

查看试题解析
20. 若关于 $x$ ， $y$ 方程组的 ${\begin{array}{l} a_{1} x + b_{1} y = c_{1} \\ a_{2} x + b_{2} y = c_{2} \end{array}$ 解为 ${\begin{array}{l} x = 5 \\ y = 6 \end{array}$ ，则方程组 ${\begin{array}{l} 5 a_{1} (x - 1) + 3 b_{1} (y + 1) = 4 c_{1} \\ 5 a_{2} (x - 1) + 3 b_{2} (y + 1) = 4 c_{2} \end{array}$ 的解为.

查看试题解析

三、解答题

21. 计算：

(1)、 $- 2^{2} + {(\sqrt{2} - 3)}^{0} - {(- \frac{1}{2})}^{- 1}$

(2)、 $(10 a^{4} b - 20 a^{2} b^{2}) \div 4 a^{2} b$

查看试题解析
22. 解方程组

(1)、 ${\begin{array}{l} 3 x + 5 y = 8 \\ 2 x - y = 1 \end{array}$

(2)、 ${\begin{array}{l} \frac{x}{4} - \frac{y}{3} = \frac{5}{6} \\ \frac{x}{3} + \frac{y}{2} = \frac{1}{6} \end{array}$

查看试题解析
23. 如图， $∠ A E D = ∠ C$ ， $∠ 1 = ∠ B$ ，说明： $E F / / A B$ .

查看试题解析
24. 如图，某工程队从A点出发，沿北偏西67°方向修一条公路AD，在BD路段出现塌陷区，就改变方向，由B点沿北偏东23°的方向继续修建BC段，到达C点又改变方向，从C点继续修建CE段，若使所修路段CE∥AB，∠ECB应为多少度？试说明理由.此时CE与BC有怎样的位置关系？

以下是小刚不完整的解答，请帮她补充完整.

解：由已知，根据

得∠1=∠A=67°

所以，∠CBD=23°+67°=°；

根据

当∠ECB+∠CBD=°时，可得CE∥AB.

所以∠ECB=°

此时CE与BC的位置关系为.

查看试题解析
25. 在解方程组 ${\begin{matrix} a x + 5 y = 10 \\ 4 x - b y = - 4 \end{matrix}$ 时，由于粗心，甲看错了方程组中的a，得到的解为 ${\begin{matrix} x = - 3 \\ y = - 1 \end{matrix}$ ，乙看错了方程组中的b，得到的解为 ${\begin{matrix} x = 5 \\ y = 4 \end{matrix}$ ．

(1)、求正确的a，b的值；

(2)、求原方程组的解．

查看试题解析
26. $Δ A B C$ 在网格中的位置如图所示，请根据下列要求解答：

(1)、①过点 $C$ 作 $A B$ 的平行线；
②过点 $A$ 作 $B C$ 的垂线段，垂足为 $D$ ；

③比较 $A B$ 和 $A D$ 的大小，并说明理由；

④将 $Δ A B C$ 先向下平移5格，再向右平移6格得到 $Δ E F G$ （点 $A$ 的对应点为点 $E$ ，点 $B$ 的对应点为点 $F$ ，点 $C$ 的对应点为点 $G$ ）.

查看试题解析
27. 如图，已知 $A B / / C D$ ，分别探讨下面的四个图形中 $∠ A P C$ 、 $∠ P A B$ 和 $∠ P C D$ 的关系，并请你从所得的四个关系中任选一个，说明成立的理由.

(1)、图①的关系是；

(2)、图②的关系是；

(3)、图③的关系是；

(4)、图④的关系是；

查看试题解析
28. 某铁件加工厂用如图1的长方形和正方形铁片(长方形的宽与正方形的边长相等)加工成如图2的竖式与横式两种无盖的长方体铁容器.(加工时接缝材料不计)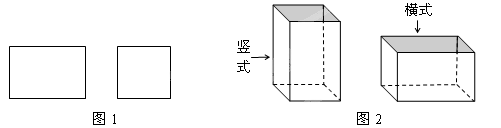

(1)、如果加工竖式铁容器与横式铁容器各1个，则共需要长方形铁片张，正方形铁片张.

(2)、现有长方形铁片2014张，正方形铁片1176张，如果加工成这两种铁容器，刚好铁片全部用完，那么加工的竖式铁容器、横式铁容器各有多少个?

(3)、把长方体铁容器加盖可以加工成为铁盒.现用35张铁板做成与如图相同的长方形铁片和正方形铁片，已知每张铁板可做成3个长方形铁片或4个正方形铁片，也可以将一张铁板做成1个长方形铁片和2个正方形铁片.该如何充分利用这些铁板加工成铁盒，最多可以加工成多少个铁盒?

查看试题解析