重庆市2019年数学中考冲刺试卷(四）

试卷更新日期：2020-03-10 类型：中考模拟

进入出卷网下载

一、单选题

1. 夏新同学上午卖废品收入13元，记为+13元，下午买旧书支出9元，记为（）元.

A、+4 B、﹣9 C、﹣4 D、+9

查看试题解析
2. 下列计算正确的是（）.

A、 $3 a - a = 2$ B、 $a^{2} \cdot a^{3} = a^{6}$ C、 ${(a + b)}^{2} = a^{2} + b^{2}$ D、 $a^{2} + 2 a^{2} = 3 a^{2}$

查看试题解析
3. 下列调查中，适宜采用全面调查（普查）方式的是（（）

A、对一批圆珠笔使用寿命的调查 B、对韩江水质现状的调查 C、对某品牌烟花爆竹燃放安全的调查 D、对一枚用于发射于卫星的运载火箭各零部件的检查

查看试题解析
4. 下列扑克牌中，中心对称图形有 $($ $)$

A、1张 B、2张 C、3张 D、4张

查看试题解析
5. 在一个不透明的袋子里装有两个黄球和一个白球，它们除颜色外都相同，随机从中摸出一个球，记下颜色后放回袋子中，充分摇匀后，再随机摸出一个球．两次都摸到黄球的概率是（）

A、 $\frac{4}{9}$ B、 $\frac{1}{3}$ C、 $\frac{2}{9}$ D、 $\frac{1}{9}$

查看试题解析
6. 为估计池塘两岸A，B间的距离，小明的办法是在地面上取一点O，连接OA，OB，测得OB=15.1m，OA=25.6m.这样小明估算出A，B间的距离不会大于（）

A、26m B、38m C、40m D、41m

查看试题解析
7. 某商场把一个双肩背包按进价提高 $50 %$ 标价，然后再按标价八折出售，这样商场每卖出一个书包仍可赢利8元，则这款双肩包的进价是（）

A、16元 B、24元 C、30元 D、40元

查看试题解析
8. “圆材埋壁”是我国著名的数学著作《九章算术》中的一个问题，“今有圆材，埋于壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？” 用现代的数学语言表达是：“如图，CD是⊙O的直径，弦AB⊥CD，垂足为E，CE = 1寸，AB = 1尺，求直径的长”. 依题意，CD长为（）

A、 $\frac{25}{2}$ 寸 B、13寸 C、25寸 D、26寸

查看试题解析
9. 在某次海上搜救工作中，A船发现在它的南偏西30°方向有一漂浮物，同时在A船正东10km处的B船发现该漂浮物在它的南偏西60°方向，此时，B船到该漂浮物的距离是（　　）

A、5 $\sqrt{3}$ km B、10 $\sqrt{3}$ km C、10km D、20km

查看试题解析
10. 关于 $x$ 的不等式组 ${\begin{array}{l} x \leq - \frac{1}{2} \\ x > m \end{array}$ 的所有整数解的积为2，则 $m$ 的取值范围为（）

A、 $m > - 3$ B、 $m < - 2$ C、 $- 3 \leq m < - 2$ D、 $- 3 < m \leq - 2$

查看试题解析
11. 如图，一段抛物线：y=﹣x（x﹣2）（0≤x≤2）记为C₁ ，它与x轴交于两点O，A₁；将C₁绕A₁旋转180°得到C₂ ，交x轴于A₂；将C₂绕A₂旋转180°得到C₃ ，交x轴于A₃；…如此进行下去，直至得到C₂₀₁₈ ，若点P（4035，m）在第2018段抛物线C₂₀₁₈上，则m的值是（）

A、1 B、－1 C、0 D、4035

查看试题解析
12. 如图，在 $△ A B C$ 中， $A C = 50 m$ ， $B C = 40 m$ ， $∠ C = 90^{\circ}$ ，点P从点A开始沿AC边向点C以 $2 m / s$ 的速度匀速移动，同时另一点Q由C点开始以 $3 m / s$ 的速度沿着射线CB匀速移动，当 $△ P C Q$ 的面积等于 $300 m^{2}$ 运动时间为 $($ $)$

A、5秒 B、20秒 C、5秒或20秒 D、不确定

查看试题解析

二、填空题

13. 计算：(3－π)⁰＋(－0.2)^－2＝.

查看试题解析
14. 现有两张铁片：长方形铁皮长为x+2y，宽为x﹣2y（其中x﹣2y＞0）；正方形铁皮的边长为2（x﹣y），根据需要把两张铁皮裁剪后焊接成一张长方形的铁片，铁皮一边长为6x，则新铁片的另一边长为（不计损失）

查看试题解析
15. 已知，在△ABC中，∠A＞∠B，分别以点A，C为圆心，大于 $\frac{1}{2}$ AC长为半径画弧，两弧交于点P，点Q，作直线PQ交AB于点D，再分别以点B，D为圆心，大于 $\frac{1}{2}$ BD长为半径画弧，两弧交于点M，点N，作直线MN交BC于点E，若△CDE是等边三角形，则∠A= ．

查看试题解析
16. 如图，这是一幅长为3m，宽为2m的长方形世界杯宣传画，为测量宣传画上世界杯图案的面积，现将宣传画平铺在地上，向长方形宣传画内随机投掷骰子（假设骰子落在长方形内的每一点都是等可能的），经过大量重复投掷试验，发现骰子落在世界杯图案中的频率稳定在常数0.4附近，由此可估计宣传画上世界杯图案的面积约为m² ．

查看试题解析
17. 小明到商场购买某个牌子的铅笔 $x$ 支，用了 $y$ 元（ $y$ 为整数）.后来他又去商场时，发现这种牌子的铅笔降价 $20 %$ ，于是他比上一次多买了 $10$ 支铅笔，用了 $4$ 元钱，那么小明两次共买了铅笔支.

查看试题解析
18. 大于1的正整数 $m$ 的三次方可“分裂”成若干个连续奇数的和， $2^{3} = 3 + 5$ ， $3^{3} = 7 + 9 + 11$ ， $4^{3} = 13 + 15 + 17 + 19$ ，…，若 $m^{3}$ 分裂后，其中有一个奇数是1007，则 $m$ 的值是．

查看试题解析

三、解答题

19. 已知：如图，在等边△ABC 中，DB 是 AC 边上的高，E 是 BC 延长线上一点，且 DB＝DE，求∠E 的度数.

查看试题解析
20.

(1)、计算： $(a + 1) (a - 1) - {(a - 2)}^{2}$ ；

(2)、解不等式： $x - 1 \geq \frac{x - 2}{2} + 3$

查看试题解析
21. 2018年12月份，我市迎来国家级文明城市复查，为了了解学生对文明城市的了解情况，学校随机抽取了部分学生进行问卷调查，将调查结果按照“A非常了解 $. B$ 了解 $. C$ 了解较少 $. D$ 不了解”四类分别统计，并绘制了下列两幅统计图(不完整 $) .$ 请根据图中信息，解答下列问题：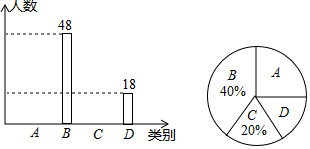

(1)、此次共调查了名学生；

(2)、扇形统计图中D所在的扇形的圆心角为；

(3)、将条形统计图补充完整；

(4)、若该校共有800名学生，请你估计对文明城市的了解情况为“非常了解”的学生的人数.

查看试题解析
22. 如图，直线y=﹣x+1与x轴，y轴分别交于B，A两点，动点P在线段AB上移动，以P为顶点作∠OPQ=45°交x轴于点Q.

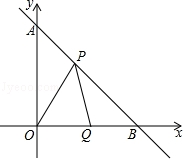(1)、求点A和点B的坐标；

(2)、比较∠AOP与∠BPQ的大小，说明理由.

(3)、是否存在点P，使得△OPQ是等腰三角形？若存在，请求出点P的坐标；若不存在，请说明理由.

查看试题解析
23. 某学校准备采购一批茶艺耗材和陶艺耗材.经查询，如果按照标价购买两种耗材，当购买茶艺耗材的数量是陶艺耗材数量的2倍时，购买茶艺耗材共需要18000元，购买陶艺耗材共需要12000元，且一套陶艺耗材单价比一套茶艺耗材单价贵150元.

(1)、求一套茶艺耗材、一套陶艺耗材的标价分别是多少元？

(2)、学校计划购买相同数量的茶艺耗材和陶艺耗材.商家告知，因为周年庆，茶艺耗材的单价在标价的基础上降价2 $m$ 元，陶艺耗材的单价在标价的基础降价150元，该校决定增加采购数量，实际购买茶艺耗材和陶艺耗材的数量在原计划基础上分别增加了2.5 $m$ %和 $m ％$ ，结果在结算时发现，两种耗材的总价相等，求 $m$ 的值.

查看试题解析
24. 如图，等腰直角△ABC中，CA=CB，点E为△ABC外一点，CE=CA，且CD平分∠ACB交AE于D，且∠CDE=60°．

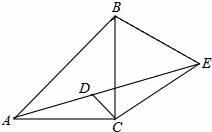(1)、求证：△CBE为等边三角形；

(2)、若AD=5，DE=7，求CD的长．

查看试题解析
25. 阅读材料：各类方程的解法
求解一元一次方程，根据等式的基本性质，把方程转化为x=a的形式.求解二元一次方程组，把它转化为一元一次方程来解；类似的，求解三元一次方程组，把它转化为解二元一次方程组.求解一元二次方程，把它转化为两个一元一次方程来解.求解分式方程，把它转化为整式方程来解，由于“去分母”可能产生增根，所以解分式方程必须检验.各类方程的解法不尽相同，但是它们有一个共同的基本数学思想 $- -$ 转化，把未知转化为已知.

用“转化”的数学思想，我们还可以解一些新的方程.例如，一元三次方程x³+x²-2x=0，可以通过因式分解把它转化为x(x²+x-2)=0，解方程x=0和x²+x-2=0，可得方程x³+x²-2x=0的解.

(1)、问题：方程x³+x²-2x=0的解是x₁=0，x₂= ， x₃=；

(2)、拓展：用“转化”思想求方程 $\sqrt{2 x + 3} = x$ 的解；

(3)、应用：如图，已知矩形草坪ABCD的长AD=8m，宽AB=3m，小华把一根长为10m的绳子的一端固定在点B，沿草坪边沿BA，AD走到点P处，把长绳PB段拉直并固定在点P，然后沿草坪边沿PD、DC走到点C处，把长绳剩下的一段拉直，长绳的另一端恰好落在点C.求AP的长.

查看试题解析
26. 如图，二次函数y＝ax²+bx+ $\sqrt{3}$ 的图象经过A（﹣1，0），B（3，0），与y轴相交于点C．点P为第一象限的抛物线上的一个动点，过点P分别做BC和x轴的垂线，交BC于点E和F，交x轴于点M和N．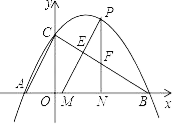

(1)、求这个二次函数的解析式；

(2)、求线段PE最大值，并求出线段PE最大时点P的坐标；

(3)、若S_△_PMN＝3S_△_PEF时，求出点P的坐标．

查看试题解析