浙江省嘉兴市嘉善县2019年数学中考三模试卷

试卷更新日期：2020-03-10 类型：中考模拟

进入出卷网下载

一、单选题

1. -2的倒数是（）

A、-2 B、 $- \frac{1}{2}$ C、 $\frac{1}{2}$ D、2

查看试题解析
2. 2018年嘉兴市实现GDP总量4853亿元，位居浙江省第六，4853亿用科学记数法表示正确的是（）

A、 4.853×10¹¹ B、4.853×10¹⁰ C、0.4853×10¹² D、0.4853×10¹¹

查看试题解析
3. 下列图形中，既是轴对称又是中心对称的图形是（）

A、正三角形 B、矩形 C、平行四边形 D、正五边形

查看试题解析
4. 大于 $\sqrt{7}$ 的最小整数是（）

A、1 B、2 C、3 D、4

查看试题解析
5. 若a＞b，则下列各式中一定成立的是（）

A、b＞a B、a﹣c＞b﹣c C、ac＞bc D、 $\frac{a}{c} > \frac{b}{c}$

查看试题解析
6. 如图，等边△AOB中，点B在x轴正半轴上，点A坐标为（1， $\sqrt{3}$ ），将△AOB绕点O顺时针旋转15°，此时点A对应点A′的坐标是（）

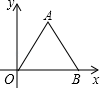A、（2，2） B、（ $\sqrt{3}$ ，1） C、 $(\frac{3}{2} ， \frac{3}{2})$ D、（ $\sqrt{2}$ ， $\sqrt{2}$ ）

查看试题解析
7. 某中学对2016年、2017年、2018年住校人数统计发现，2017年比2016年增加20%，2018年比2017年减少20%，那么2018年比2016年（）

A、增加4% B、减少4% C、减少2% D、不增不减

查看试题解析
8. 已知Rt△ABC中，∠C＝90°，若BC＝a，AC＝b，AB＝c，且a²﹣ab﹣2b²＝0，则a：b：c＝（）

A、1：2： $\sqrt{5}$ B、2：1： $\sqrt{5}$ C、1：2： $\sqrt{3}$ D、2：1： $\sqrt{3}$

查看试题解析
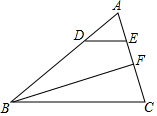9. 如图，在△ABC中，BC＝9，∠ABC的平分线BF交AC于点F，点D、点E分别是边AB、AC上的点，若 $\frac{A D}{A B} = \frac{A E}{A C} = \frac{E F}{E C} = \frac{1}{3}$ ，则BD﹣DE的值为（）

A、3 B、3.5 C、4 D、4.5

查看试题解析
10. 在平面直角坐标系中，已知点A（1，2）和点B（4，5），当直线y＝kx﹣2k（k为常数）与线段AB有交点时，k的取值范围为（）

A、k≤﹣2或k≥ $\frac{5}{2}$ B、﹣2≤k≤ $\frac{5}{2}$ C、﹣2≤k≤0或0≤k≤ $\frac{5}{2}$ D、﹣2＜k＜0或0＜k＜ $\frac{5}{2}$

查看试题解析

二、填空题

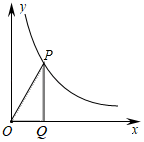
11. 分解因式：a²﹣1＝．

查看试题解析
12. 如图，在平面直角坐标系中，点P是函数y＝ $\frac{k}{x}$ （x＞0）图象上的一点，作PQ⊥x轴于点Q，连结OP，若△OPQ的面积等于2，则k的值是.

查看试题解析
13. 如图，网格中小正方形的边长为1，点A、B、C都落在格点上，则sinA＝.

查看试题解析
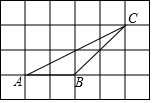14. 如图，圆柱的侧面是由一张长16πcm、宽3cm的长方形纸条围成（接缝处重叠部分忽略不计），那么该圆柱的体积是cm³.

查看试题解析
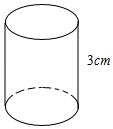15. 在矩形ABCD中，∠ABC的平分线交边AD于点E，∠BED的平分线交直线CD于点F.若AB＝3，CF＝1，则BC＝.

查看试题解析
16. 如图，在平面直角坐标系中，正方形ABCD的顶点A与原点O重合，顶点B在直线l上，将正方形沿射线OB方向无滑动地翻滚.若直线 $y = \frac{\sqrt{3}}{3} x$ ，正方形边长为2 $\sqrt{3}$

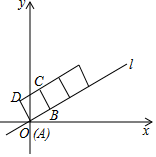(1)、翻滚后点A第一次落在直线l上的坐标是；

(2)、当正方形翻滚2002次点A对应点的坐标是.

查看试题解析

三、解答题

17.

(1)、计算：2sin30°+（2﹣π）⁰﹣ ${(\frac{1}{3})}^{- 1}$ ；

(2)、解方程：2x²+x﹣6＝0.

查看试题解析
18. 先化简，再求值： $(1 - \frac{1}{a + 1}) \cdot \frac{a^{2} + 2 a + 1}{a}$ ，其中a ＝ $\sqrt{2}$ －1.

查看试题解析
19. 如图，已知△ABC中，D是BC的中点，DE⊥AB于E，DF⊥AC于F，且DE＝DF.试说明AB＝AC的理由.

查看试题解析

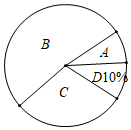
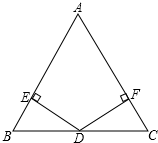20. 嘉善县将开展以“珍爱生命，铁拳护航”为主题的交通知识竞赛，某校对参加选拔赛的若干名同学的成绩按A，B，C，D四个等级进行统计，绘制成如下不完整的频数统计表和扇形统计图

成绩等级	频数（人数）	频率
A	4	0.08
B	m	0.52
C		n
D
合计		1

(1)、求m＝， n＝；

(2)、在扇形统计图中，求“C等级”所对应圆心角的度数；

(3)、“A等级”的4名同学中有3名男生和1名女生，现从中随机挑选2名同学代表学校参加全县比赛，请用树状图法或列表法求出恰好选中“一男一女”的概率.

查看试题解析

21. （阅读材料）在平面直角坐标系中，点P（x₀ ， y₀）到直线Ax+By+C＝0的距离公式是 $d = \frac{| {Ax}_{0} + {By}_{0} + C |}{\sqrt{A^{2} + B^{2}}}$
如：求点P（1，2）到直线y＝﹣ $\frac{4}{3}$ x+1的距离d

解：将直线解析式变形为4x+3y﹣3＝0，则A＝4，B＝3，C＝﹣3

所以 $d = \frac{| 4 \times 1 + 3 \times 2 - 3 |}{\sqrt{4^{2} + 3^{2}}} = \frac{7}{5}$

（解决问题）已知直线l₁的解析式是y＝- $\frac{1}{2}$ x+1

(1)、若点P的坐标为（1，﹣2），则点P到直线l₁的距离是；

(2)、若直线l₂与直线l₁平行，且两条平行线间的距离是 $\sqrt{5}$ ，请求出直线l₂的解析式.

查看试题解析
22. 在某县美化城市工程招投标中，有甲、乙两个工程队投标经测算：甲队单独完成这项工程需要30天，若由甲队先做10天，剩下的工程由甲、乙合作12天可完成.问：

(1)、乙队单独完成这项工程需要多少天？

(2)、甲队施工一天需付工程款3.5万元，乙队施工一天需工程款2万元，该工程计划用时不超过35天，在不超过计划天数的前提下，由甲队先单独施工若干天，剩下的工程由乙队单独完成，那么安排甲队单独施工多少天工程款最省？最省的工程款是多少万元？

查看试题解析
23. 已知点P是抛物线 $y = \frac{1}{8} x^{2} + 1$ 上的任意一点，设点P到直线y＝﹣1的距离为d₁ ，点P到点F（0，3）的距离为d₂

(1)、求抛物线的顶点坐标和对称轴；

(2)、判断d₁ ， d₂的大小关系并证明；

(3)、若线段PF的延长线交抛物线于点Q，且线段PQ的长度是m，线段PQ的中点M到x轴的距离是n.直接写出m与n关系式.

查看试题解析
24. 如图，分别以△ABC的边AB、AC为一边，向外作正方形ABEF和正方形AGHC像这样的两个正方形称为△ABC的“依伴正方形”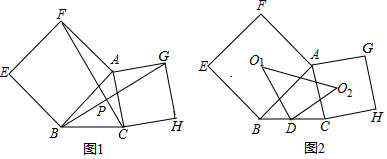

(1)、如图1，连接BG，CF相交于点P，求证：BG＝CF且BG⊥CF；

(2)、如图2，点D是BC的中点，两个依伴正方形的中心分别为O₁ ， O₂连结O₁D，O₂D，O₁O₂：，判断△DO₁O₂的形状并说明由；

(3)、如图2，若AB＝6，AC＝ $\sqrt{3}$ ，∠BAC＝60°，求O₁O₂的长.

查看试题解析