浙江省杭州市萧山区2019年数学中考一模试卷
试卷更新日期:2020-03-10 类型:中考模拟
一、单选题
-
1. 计算﹣3+2=( )A、﹣1 B、1 C、﹣5 D、52. 已知买 千克苹果共花了 元,则买2千克苹果要花( )元.A、 B、 C、 D、3. 某景区在“五一”小长假期间,每天接待的旅客人数统计如下表.
日期
5月1日
5月2日
5月3日
5月4日
5月5日
人数(万人)
1.2
2
2.5
2
1.1
表中表示人数的一组数据中,众数和中位数分别为( )
A、2.5万,2万 B、2.5万,2.5万 C、2万,2.5万 D、2万,2万4. 如图,将一正方形纸片沿图(1)、( 2)的虚线对折,得到图(3),然后沿图(3)中虚线的剪去一个角,展开得平面图形(4),则图(3)的虚线是( )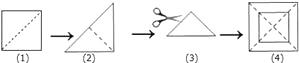 A、
A、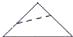 B、
B、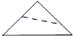 C、
C、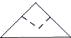 D、
D、 5. 如图,Rt△ABC中,∠ACB=90°,点D是BC边上一点.若∠B=α,∠ADC=β,则 为( )
5. 如图,Rt△ABC中,∠ACB=90°,点D是BC边上一点.若∠B=α,∠ADC=β,则 为( ) A、 B、 C、 D、6. 某公司第4月份投入1000万元科研经费,计划6月份投入科研经费比4月多500万元.设该公司第5、6个月投放科研经费的月平均增长率为x,则所列方程正确的为( )A、1000(1+x)2=1000+500 B、1000(1+x)2=500 C、500(1+x)2=1000 D、1000(1+2x)=1000+5007. 如图,菱形ABCD中,边CD的中垂线交对角线BD于点E,交CD于点F,连结AE.若∠ABC=50°,则∠AEB的度数为( )
A、 B、 C、 D、6. 某公司第4月份投入1000万元科研经费,计划6月份投入科研经费比4月多500万元.设该公司第5、6个月投放科研经费的月平均增长率为x,则所列方程正确的为( )A、1000(1+x)2=1000+500 B、1000(1+x)2=500 C、500(1+x)2=1000 D、1000(1+2x)=1000+5007. 如图,菱形ABCD中,边CD的中垂线交对角线BD于点E,交CD于点F,连结AE.若∠ABC=50°,则∠AEB的度数为( ) A、30° B、40° C、50° D、60°8. 如图,记图①中阴影部分面积为 ,图②中阴影部分面积为 ,设 ,则( )
A、30° B、40° C、50° D、60°8. 如图,记图①中阴影部分面积为 ,图②中阴影部分面积为 ,设 ,则( )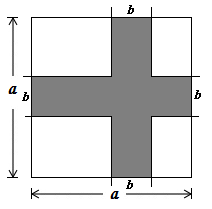

图① 图②
A、 B、 C、 D、9. 已知点(﹣3,y1),(5,y2)在二次函数y=ax2+bx+c(a≠0)的图象上,点(x0 , y0)是函数图象的顶点.则( )A、当y1>y2≥y0时,x0的取值范围是1<x0<5 B、当y1>y2≥y0时,x0的取值范围是x0>5 C、当y0≥y1>y2时,x0的取值范围是x0<﹣3 D、当y0≥y1>y2时,x0的取值范围是x0<110. 如图,△ABC中,D为边AB上一点,E是CD的中点,且∠ACD=∠ABE.已知AC=2,设AB=x,AD=y,则y与x满足的关系式为( ) A、xy=4 B、2xy﹣y2=4 C、xy﹣y2=4 D、x2+xy﹣2y2=4
A、xy=4 B、2xy﹣y2=4 C、xy﹣y2=4 D、x2+xy﹣2y2=4二、填空题
-
11. 计算:a5÷(﹣a)3=.12. 如图,直线a∥b,直线a,b被直线c所截若∠1=2∠2,则∠2的度数为.
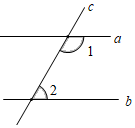 13. 一个盒子里装有除颜色外都相同的10个球,其中有a个红球,b个黄球,3个白球.从盒子里随意摸出1个球,摸出黄球的概率是 ,那么a= , b=.14. 如图,Rt△ABC中,∠ABC=90°,点D是BC边上一点,以BD为直径的半圆与边AC相切于点E.若AB=3,BC=4,则BD=.
13. 一个盒子里装有除颜色外都相同的10个球,其中有a个红球,b个黄球,3个白球.从盒子里随意摸出1个球,摸出黄球的概率是 ,那么a= , b=.14. 如图,Rt△ABC中,∠ABC=90°,点D是BC边上一点,以BD为直径的半圆与边AC相切于点E.若AB=3,BC=4,则BD=.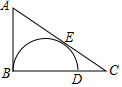 15. 已知直线y=3x﹣2经过点A(a,b),B(a+m,b+k),其中k≠0,则 的值为.16. 如图,线段AB=a,点P是AB中垂线MN上的一动点,过点P作直线CD∥AB.若在直线CD上存在点Q使得△ABQ为等腰三角形,且满足条件的点Q有且只有3个,则PM的长为.
15. 已知直线y=3x﹣2经过点A(a,b),B(a+m,b+k),其中k≠0,则 的值为.16. 如图,线段AB=a,点P是AB中垂线MN上的一动点,过点P作直线CD∥AB.若在直线CD上存在点Q使得△ABQ为等腰三角形,且满足条件的点Q有且只有3个,则PM的长为.
三、解答题
-
17. 萧山区垃圾分类掀起“绿色革命”为调查居民对垃圾分类的了解情况,调查小组对某小区进行抽样调查并将调查结果绘制成了统计图(如图).已知调查中“基本了解”的人数占调查人数的60%.
 (1)、计算此次调查人数,并补全统计图;(2)、若该小区有住户1000人,请估计该小区对垃圾分类“基本了解”的人数.18. 已知M=x2﹣3,N=4(x﹣ ).(1)、当x=﹣1时,求M﹣N的值;(2)、当1<x<2时,试比较M,N的大小.19. 如图,△ABC中,AB=AC,AD⊥BC于点D,DE⊥AC于点E,CF⊥AB于点F.
(1)、计算此次调查人数,并补全统计图;(2)、若该小区有住户1000人,请估计该小区对垃圾分类“基本了解”的人数.18. 已知M=x2﹣3,N=4(x﹣ ).(1)、当x=﹣1时,求M﹣N的值;(2)、当1<x<2时,试比较M,N的大小.19. 如图,△ABC中,AB=AC,AD⊥BC于点D,DE⊥AC于点E,CF⊥AB于点F. (1)、求证:△BCF∽△CDE;(2)、若DE=3,求CF的长.20. 已知一次函数y1=kx+b的图象与反比例函数y2= 的图象交于点A(2,2),B(﹣1,a)(1)、求一次函数和反比例函数的表达式;(2)、设点P(h,y1),Q(h,y2)分别是两函数图象上的点;
(1)、求证:△BCF∽△CDE;(2)、若DE=3,求CF的长.20. 已知一次函数y1=kx+b的图象与反比例函数y2= 的图象交于点A(2,2),B(﹣1,a)(1)、求一次函数和反比例函数的表达式;(2)、设点P(h,y1),Q(h,y2)分别是两函数图象上的点;①试直接写出当y1>y2时h的取值范围;
②若y1﹣y2=2,试求h的值.
21. 如图,矩形ABCD中,BC>AB,E是AD上一点,△ABE沿BE折叠,点A恰好落在线段CE的点F处,连结BF. (1)、求证:BC=CE;(2)、设 =k.
(1)、求证:BC=CE;(2)、设 =k.①若k= ,求sin∠DCE的值;
②设 =m,试求m与k满足的关系式.
22. 已知二次函数y=x2﹣(2m+1)x﹣3m.(1)、若m=2,写出该函数的表达式,并求出函数图象的对称轴.(2)、已知点P(m,y1),Q(m+4,y2)在该函数图象上,试比较y1 , y2的大小.(3)、对于此函数,在﹣1≤x≤1的范围内至少有x值使得y≥0,求m的取值范围.23. 如图,已知AB是⊙O的直径,弦CD⊥AB于点E.点P是劣弧 上任一点(不与点A,D重合),CP交AB于点M,AP与CD的延长相交于点F.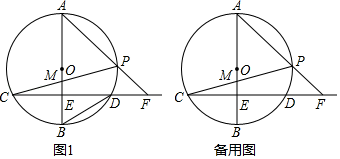 (1)、设∠CPF=α,∠BDC=β,求证:α=β+90°;(2)、若OE=BE,设tan∠AFC=x, .①求∠APC的度数;
(1)、设∠CPF=α,∠BDC=β,求证:α=β+90°;(2)、若OE=BE,设tan∠AFC=x, .①求∠APC的度数;②求y关于x的函数表达式及自变量x的取值范围.