浙江省杭州市2020年数学中考一模试卷
试卷更新日期:2020-03-10 类型:中考模拟
一、单选题
-
1.
如图,四个有理数在数轴上的对应点M,P,N,Q,若点M,N表示的有理数互为相反数,则图中表示绝对值最小的数的点是( )
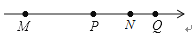 A、点M B、点N C、点P D、点Q2. 长兴是浙江省的北大门,与苏、皖两省接壤,位于太湖西南岸,全县区域面积1430平方公里,现有户籍人口约64万.将1430用科学记数法表示为( )A、0.143×104 B、1.43×103 C、14.3×102 D、143×103. 下列图形中,是中心对称图形又是轴对称图形的是( )A、
A、点M B、点N C、点P D、点Q2. 长兴是浙江省的北大门,与苏、皖两省接壤,位于太湖西南岸,全县区域面积1430平方公里,现有户籍人口约64万.将1430用科学记数法表示为( )A、0.143×104 B、1.43×103 C、14.3×102 D、143×103. 下列图形中,是中心对称图形又是轴对称图形的是( )A、 B、
B、 C、
C、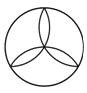 D、
D、 4. 在我市举行的中学生春季田径运动会上,参加男子跳高的15名运动员的成绩如下表所示:
4. 在我市举行的中学生春季田径运动会上,参加男子跳高的15名运动员的成绩如下表所示:成绩(m) 1.50 1.60 1.65 1.70 1.75 1.80 人数 1 2 4 3 3 2 这些运动员跳高成绩的中位数和众数分别是()
A、1.70,1.65 B、1.70,1.70 C、1.65,1.70 D、3,45. 下列运算中,正确的是( )A、3a2﹣a2=2 B、(a2)3=a5 C、a2•a3=a5 D、(2a2)2=2a46. 《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.意思是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相等.两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计).问黄金、白银每枚各重多少两?设每枚黄金重x两,每枚白银重y两,根据题意得( )A、 B、 C、 D、7. 如图,AB∥GH∥CD,点H在BC上,AC与BD交于点G,AB=2,CD=3,则GH长为( ) A、1 B、1.2 C、2 D、2.58. 解分式方程 ,正确的结果是( )A、x=0 B、x=1 C、x=2 D、无解9. 如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标(1,n),与y轴的交点在(0,3),(0,4)之间(包含端点),则下列结论:①abc>0;②3a+b<0;③﹣ ≤a≤﹣1;④a+b≥am2+bm(m为任意实数);⑤一元二次方程ax2+bx+c=n有两个不相等的实数根,其中正确的有( )
A、1 B、1.2 C、2 D、2.58. 解分式方程 ,正确的结果是( )A、x=0 B、x=1 C、x=2 D、无解9. 如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标(1,n),与y轴的交点在(0,3),(0,4)之间(包含端点),则下列结论:①abc>0;②3a+b<0;③﹣ ≤a≤﹣1;④a+b≥am2+bm(m为任意实数);⑤一元二次方程ax2+bx+c=n有两个不相等的实数根,其中正确的有( )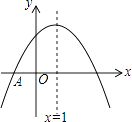 A、2个 B、3个 C、4个 D、5个10. 如图,在矩形ABCD中,AD= AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:
A、2个 B、3个 C、4个 D、5个10. 如图,在矩形ABCD中,AD= AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF,
其中正确的有( )
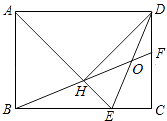 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
11. 因式分解: .12. 规定: ,如: ,若 ,则 =.13. 从分别标有1、2、3、4的四张卡片中,一次同时抽2张,其中和为奇数的概率是.14. 已知AB是⊙O的直径,弦CD⊥AB于点E,弦PQ∥AB交弦CD于点M,BE=18,CD=PQ=24,则OM的长为.
 15. 图甲是小明设计的带菱形图案的花边作品,该作品由形如图乙的矩形图案拼接而成(不重叠,无缝隙).图乙种, ,EF=4cm,上下两个阴影三角形的面积之和为54cm2 , 其内部菱形由两组距离相等的平行线交叉得到,则该菱形的周长为cm
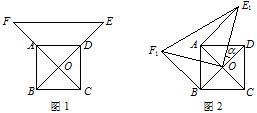
15. 图甲是小明设计的带菱形图案的花边作品,该作品由形如图乙的矩形图案拼接而成(不重叠,无缝隙).图乙种, ,EF=4cm,上下两个阴影三角形的面积之和为54cm2 , 其内部菱形由两组距离相等的平行线交叉得到,则该菱形的周长为cm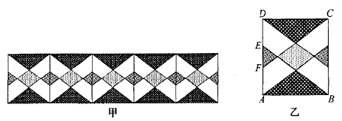 16. 如图所示,Rt△AOB中,∠AOB=90°,OA=4,OB=2,点B在反比例函数y= 图象上,则图中过点A的双曲线解析式是.
16. 如图所示,Rt△AOB中,∠AOB=90°,OA=4,OB=2,点B在反比例函数y= 图象上,则图中过点A的双曲线解析式是.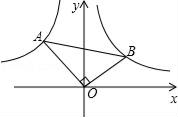
三、解答题
-
17. “分组合作学习”成为我市推动课堂教学改革,打造自主高效课堂的重要举措.某中学从全校学生中随机抽取100人作为样本,对“分组合作学习”实施前后学生的学习兴趣变化情况进行调查分析,统计如下:
分组前学生学习兴趣 分组后学生学习兴趣
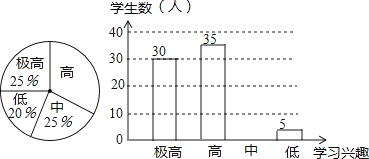
请结合图中信息解答下列问题:
(1)、求出分组前学生学习兴趣为“高”的所占的百分比为;(2)、补全分组后学生学习兴趣的统计图;(3)、通过“分组合作学习”前后对比,请你估计全校2000名学生中学习兴趣获得提高的学生有多少人?请根据你的估计情况谈谈对“分组合作学习”这项举措的看法.18. 已知抛物线 ( 是常数)经过点 .
(1)、求该抛物线的解析式和顶点坐标.
(2)、抛物线与 轴另一交点为点 ,与 轴交于点 ,平行于 轴的直线 与抛物线交于点 , ,与直线 交于点 .①求直线 的解析式.
②若 ,结合函数的图象,求 的取值范围.
19. 如图,一次函数y=kx+b(k≠0)的图象与x轴,y轴分别交于A(﹣9,0),B(0,6)两点,过点C(2,0)作直线l与BC垂直,点E在直线l位于x轴上方的部分.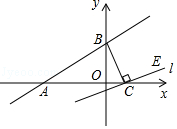 (1)、求一次函数y=kx+b(k≠0)的表达式;(2)、若△ACE的面积为11,求点E的坐标;(3)、当∠CBE=∠ABO时,点E的坐标为.20. 某化工车间发生有害气体泄漏,自泄漏开始到完全控制利用了40min,之后将对泄漏有害气体进行清理,线段DE表示气体泄漏时车间内危险检测表显示数据y与时间x(min)之间的函数关系(0≤x≤40),反比例函数y= 对应曲线EF表示气体泄漏控制之后车间危险检测表显示数据y与时间x(min)之间的函数关系(40≤x≤?).根据图象解答下列问题:
(1)、求一次函数y=kx+b(k≠0)的表达式;(2)、若△ACE的面积为11,求点E的坐标;(3)、当∠CBE=∠ABO时,点E的坐标为.20. 某化工车间发生有害气体泄漏,自泄漏开始到完全控制利用了40min,之后将对泄漏有害气体进行清理,线段DE表示气体泄漏时车间内危险检测表显示数据y与时间x(min)之间的函数关系(0≤x≤40),反比例函数y= 对应曲线EF表示气体泄漏控制之后车间危险检测表显示数据y与时间x(min)之间的函数关系(40≤x≤?).根据图象解答下列问题: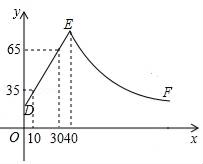 (1)、危险检测表在气体泄漏之初显示的数据是;(2)、求反比例函数y= 的表达式,并确定车间内危险检测表恢复到气体泄漏之初数据时对应x的值.21. 已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.
(1)、危险检测表在气体泄漏之初显示的数据是;(2)、求反比例函数y= 的表达式,并确定车间内危险检测表恢复到气体泄漏之初数据时对应x的值.21. 已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.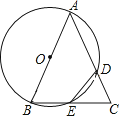 (1)、求证:AB=AC;(2)、若AB=4,BC=2 ,求CD的长.
(1)、求证:AB=AC;(2)、若AB=4,BC=2 ,求CD的长.