云南省2020年数学中考二模试卷
试卷更新日期:2020-03-10 类型:中考模拟
一、单选题
-
1. 若代数式 在实数范围内有意义,则x的取值范围是( )A、x<3 B、x≤3 C、x>3 D、x≥32. 下列几何体中,俯视图为三角形的是( )A、
 B、
B、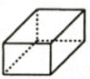 C、
C、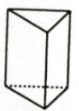 D、
D、 3. 下列计算正确的是( )A、a4+a5=a9 B、(2a2b3)2=4a4b6 C、﹣2a(a+3)=﹣2a2+6a D、(2a﹣b)2=4a2﹣b24. 在下列图形中,既是轴对称图形又是中心对称图形的是( )A、
3. 下列计算正确的是( )A、a4+a5=a9 B、(2a2b3)2=4a4b6 C、﹣2a(a+3)=﹣2a2+6a D、(2a﹣b)2=4a2﹣b24. 在下列图形中,既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、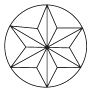 5. 某中学篮球队12名队员的年龄情况如下表,则这个队队员年龄的众数和中位数分别( )
5. 某中学篮球队12名队员的年龄情况如下表,则这个队队员年龄的众数和中位数分别( )年龄(岁)
14
15
16
17
18
人数(人)
1
4
3
2
2
A、15,16 B、15,15 C、15,15.5 D、16,156. 如图所示,直线a∥b,∠1=35°,∠2=90°,则∠3的度数为( )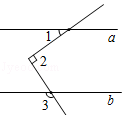 A、125° B、135° C、145° D、155°7. 如图,Rt△ABC中,∠ACB=90°,AB=5,AC=4,CD⊥AB于D,则tan∠BCD的值为( )
A、125° B、135° C、145° D、155°7. 如图,Rt△ABC中,∠ACB=90°,AB=5,AC=4,CD⊥AB于D,则tan∠BCD的值为( )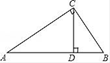 A、 B、 C、 D、8. 如图,函数 (x>0)和 (x>0)的图象分别是 和 .设点P在 上,PA∥y轴交 于点A,PB∥x轴,交 于点B,△PAB的面积为( )
A、 B、 C、 D、8. 如图,函数 (x>0)和 (x>0)的图象分别是 和 .设点P在 上,PA∥y轴交 于点A,PB∥x轴,交 于点B,△PAB的面积为( )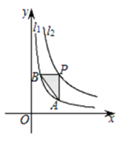 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
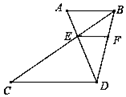
9. 的相反数是.10. 据旅游业数据显示,2018年上半年我国出境旅游超过129 000 000人次,将数据129 000 000用科学记数法表示为 .11. 若反比例函数y= 的图象经过点(-1,2),则k的值是.12. 分解因式: =.13. 如图,AB∥CD,AD、BC相交于点E,过点E作EF∥CD交BD于点F,AB:CD=2:3,那么 =.
 14. 在Rt△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,a∶b=2∶3,c= ,则a=.
14. 在Rt△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,a∶b=2∶3,c= ,则a=.三、解答题
-
15. 计算:16. 如图,∠A=∠D,∠B=∠E,AF=DC.求证:BC=EF.
 17. 孔明同学对本校学生会组织的“为贫困山区献爱心”自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据.如图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为3:4:5:10:8,又知此次调查中捐款30元的学生一共16人.
17. 孔明同学对本校学生会组织的“为贫困山区献爱心”自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据.如图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为3:4:5:10:8,又知此次调查中捐款30元的学生一共16人.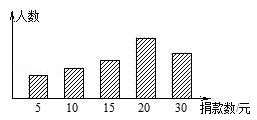 (1)、孔明同学调查的这组学生共有人;(2)、这组数据的众数是元,中位数是元;(3)、若该校有2000名学生,都进行了捐款,估计全校学生共捐款多少元?18. 在一个不透明的口袋里装有四个球,这四个球上分别标记数字﹣3、﹣1、0、2,除数字不同外,这四个球没有任何区别.(1)、从中任取一球,求该球上标记的数字为正数的概率;(2)、从中任取两球,将两球上标记的数字分别记为x、y,求点(x,y)位于第二象限的概率.19. 观察下列各式及其验证过程: ,验证: ,验证: .(1)、按照上述两个等式及其验证过程,猜想 的变形结果并进行验证;(2)、针对上述各式反映的规律,直接写出用a(a≥2的整数)表示的等式.20. 在平面直角坐标系中,抛物线y=(x﹣h)2+k的对称轴是直线x=1.(1)、若抛物线与x轴交于原点,求k的值;(2)、当﹣1<x<0时,抛物线与x轴有且只有一个公共点,求k的取值范围.21. 某电器商场销售甲、乙两种品牌空调,已知每台乙种品牌空调的进价比每台甲种品牌空调的进价高20%,用7200元购进的乙种品牌空调数量比用3000元购进的甲种品牌空调数量多2台.(1)、求甲、乙两种品牌空调的进货价;(2)、该商场拟用不超过16000元购进甲、乙两种品牌空调共10台进行销售,其中甲种品牌空调的售价为2500元/台,乙种品牌空调的售价为3500元/台.请您帮该商场设计一种进货方案,使得在售完这10台空调后获利最大,并求出最大利润.22. 如图,在△ABC中,AB=AC,以AB为直径作半圆⊙O,交BC于点D,连接AD.过点D作DE⊥AC,垂足为点E.
(1)、孔明同学调查的这组学生共有人;(2)、这组数据的众数是元,中位数是元;(3)、若该校有2000名学生,都进行了捐款,估计全校学生共捐款多少元?18. 在一个不透明的口袋里装有四个球,这四个球上分别标记数字﹣3、﹣1、0、2,除数字不同外,这四个球没有任何区别.(1)、从中任取一球,求该球上标记的数字为正数的概率;(2)、从中任取两球,将两球上标记的数字分别记为x、y,求点(x,y)位于第二象限的概率.19. 观察下列各式及其验证过程: ,验证: ,验证: .(1)、按照上述两个等式及其验证过程,猜想 的变形结果并进行验证;(2)、针对上述各式反映的规律,直接写出用a(a≥2的整数)表示的等式.20. 在平面直角坐标系中,抛物线y=(x﹣h)2+k的对称轴是直线x=1.(1)、若抛物线与x轴交于原点,求k的值;(2)、当﹣1<x<0时,抛物线与x轴有且只有一个公共点,求k的取值范围.21. 某电器商场销售甲、乙两种品牌空调,已知每台乙种品牌空调的进价比每台甲种品牌空调的进价高20%,用7200元购进的乙种品牌空调数量比用3000元购进的甲种品牌空调数量多2台.(1)、求甲、乙两种品牌空调的进货价;(2)、该商场拟用不超过16000元购进甲、乙两种品牌空调共10台进行销售,其中甲种品牌空调的售价为2500元/台,乙种品牌空调的售价为3500元/台.请您帮该商场设计一种进货方案,使得在售完这10台空调后获利最大,并求出最大利润.22. 如图,在△ABC中,AB=AC,以AB为直径作半圆⊙O,交BC于点D,连接AD.过点D作DE⊥AC,垂足为点E.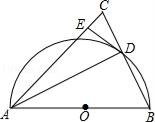 (1)、求证:DE是⊙O的切线;(2)、当⊙O半径为3,CE=2时,求BD长.23. 在直角坐标系中,过原点O及点A(8,0),C(0,6)作矩形OABC、连结OB,点D为OB的中点,点E是线段AB上的动点,连结DE,作DF⊥DE,交OA于点F,连结EF.已知点E从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒.
(1)、求证:DE是⊙O的切线;(2)、当⊙O半径为3,CE=2时,求BD长.23. 在直角坐标系中,过原点O及点A(8,0),C(0,6)作矩形OABC、连结OB,点D为OB的中点,点E是线段AB上的动点,连结DE,作DF⊥DE,交OA于点F,连结EF.已知点E从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒.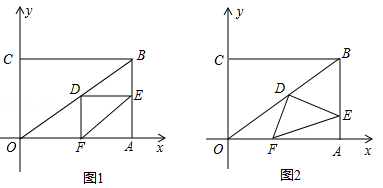 (1)、如图1,当t=3时,求DF的长.(2)、如图2,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠DEF的值.(3)、连结AD,当AD将△DEF分成的两部分的面积之比为1:2时,求相应的t的值.
(1)、如图1,当t=3时,求DF的长.(2)、如图2,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠DEF的值.(3)、连结AD,当AD将△DEF分成的两部分的面积之比为1:2时,求相应的t的值.