陕西省2020年数学中考模拟试卷
试卷更新日期:2020-03-10 类型:中考模拟
一、单选题
-
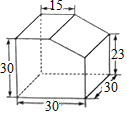
1. 计算20200的结果是( )A、2020 B、1 C、0 D、2. 如图所示的几何体,它的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 如图, ,则 的度数为( )
3. 如图, ,则 的度数为( ) A、115° B、110° C、105° D、65°4. 已知直线y=2x经过点(1,a),则a的值为( )A、a=2 B、a=-1 C、a=-2 D、a=15. 下列计算正确的是( )A、 B、 C、 D、6. 如图,在四边形ABDC中,∠B=∠D=90°,∠BAC与∠ACD的平分线交于点O,且点O在线段BD上,BD=4,则点O到边AC的距离是( )
A、115° B、110° C、105° D、65°4. 已知直线y=2x经过点(1,a),则a的值为( )A、a=2 B、a=-1 C、a=-2 D、a=15. 下列计算正确的是( )A、 B、 C、 D、6. 如图,在四边形ABDC中,∠B=∠D=90°,∠BAC与∠ACD的平分线交于点O,且点O在线段BD上,BD=4,则点O到边AC的距离是( )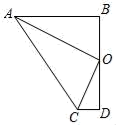 A、1 B、1.5 C、2 D、37. 将直线y=﹣2x+1向上平移2个单位长度,所得到的直线解析式为( )A、y=2x+1 B、y=﹣2x﹣1 C、y=2x+3 D、y=﹣2x+38. 如图,在矩形ABCD中,AB=8,AD=6,过点D作直线m∥AC,点E、F是直线m上两个动点,在运动过程中EF∥AC且EF=AC,四边形ACFE的面积是( )
A、1 B、1.5 C、2 D、37. 将直线y=﹣2x+1向上平移2个单位长度,所得到的直线解析式为( )A、y=2x+1 B、y=﹣2x﹣1 C、y=2x+3 D、y=﹣2x+38. 如图,在矩形ABCD中,AB=8,AD=6,过点D作直线m∥AC,点E、F是直线m上两个动点,在运动过程中EF∥AC且EF=AC,四边形ACFE的面积是( )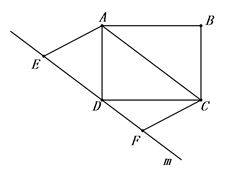 A、48 B、40 C、24 D、309. 如图,AB是⊙O的直径,点C、D在⊙O上,∠BOC=110°,AD//OC,则∠ABD等于( )
A、48 B、40 C、24 D、309. 如图,AB是⊙O的直径,点C、D在⊙O上,∠BOC=110°,AD//OC,则∠ABD等于( )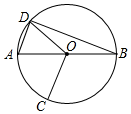 A、 B、 C、 D、10. 在同一平面直角坐标系中,若抛物线 与 关于y轴对称,则符合条件的m,n的值为( )A、m= ,n= B、m=5,n= -6 C、m= -1,n=6 D、m=1,n= -2
A、 B、 C、 D、10. 在同一平面直角坐标系中,若抛物线 与 关于y轴对称,则符合条件的m,n的值为( )A、m= ,n= B、m=5,n= -6 C、m= -1,n=6 D、m=1,n= -2二、填空题
-
11. 实数 ,﹣3, , ,0中的无理数是.12. 在半径为r的圆中,圆内接正六边形的边长为 .13. 如图,已知直线 与坐标轴交于A,B两点,矩形ABCD的对称中心为M,双曲线 (x>0)正好经过C,M两点,则直线AC的解析式为:.
 14. 如图,已知正方形ABCD的边长为8,点E是正方形内部一点,连接BE,CE,且∠ABE=∠BCE,点P是AB边上一动点,连接PD,PE,则PD+PE的长度最小值为.
14. 如图,已知正方形ABCD的边长为8,点E是正方形内部一点,连接BE,CE,且∠ABE=∠BCE,点P是AB边上一动点,连接PD,PE,则PD+PE的长度最小值为.
三、解答题
-
15. 计算: ×(﹣ )+|2﹣3 |16. 化简: ÷(x- )17. 如图,△ABC中,AB=AC,过点A作AD⊥BC于点D.
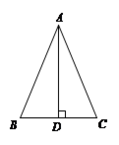 (1)、确定△ABC外接圆的圆心O,并画出△ABC的外接圆⊙O;(尺规作图,保留作图痕迹,不写作法)(2)、若BC=4,∠BAC=45°,求⊙O的半径.18. 如图,已知AF=DC,BC∥EF,∠E=∠B,求证:EF=BC.
(1)、确定△ABC外接圆的圆心O,并画出△ABC的外接圆⊙O;(尺规作图,保留作图痕迹,不写作法)(2)、若BC=4,∠BAC=45°,求⊙O的半径.18. 如图,已知AF=DC,BC∥EF,∠E=∠B,求证:EF=BC.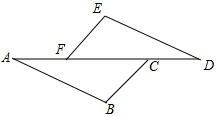 19. 甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
19. 甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图: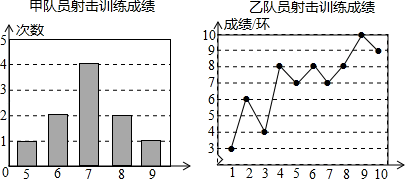
根据以上信息,整理分析数据如下:
平均成绩/环
中位数/环
众数/环
方差
甲
a
7
7
1.2
乙
7
b
8
c
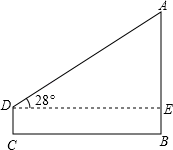
(1)、写出表格中a,b,c的值:a= , b= , c=.(2)、如果乙再射击一次,命中7环,那么乙的射击成绩的方差.(填“变大”“变小”“不变”)(3)、教练根据这10次成绩若选择甲参加比赛,教练的理由是什么?20. 某数学课外活动小组的同学.利用所学的数学知识,测底部可以到达的学校操场上的旗杆AB高度,他们采用了如下两种方法:方法1:在地面上选一点C,测得CB为40米,用高为1.6米的测角仪在C处测得旗杆顶部A的仰角为28°;
方法2:在相同时刻测得旗杆AB的影长为17.15米,又测得已有的2米高的竹杆的影长为1.5米.
你认为这两种方法可行吗?若可行,请你任选一种方法算出旗杆高度(精确到0.1米)若不可行,自己另设计一种测量方法(旗杆顶端不能到达),算出旗杆高度(结果可用字母表示)
 21. 甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线OBCDA表示轿车离甲地距离y(千米)与时间x(小时)之间的函数关系.请根据图象解答下列问题:
21. 甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线OBCDA表示轿车离甲地距离y(千米)与时间x(小时)之间的函数关系.请根据图象解答下列问题: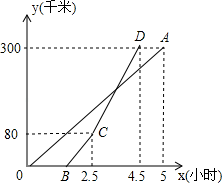 (1)、当轿车刚到乙地时,此时货车距离乙地千米;(2)、当轿车与货车相遇时,求此时x的值;(3)、在两车行驶过程中,当轿车与货车相距20千米时,求x的值.22. 小明和小亮玩一个游戏:取三张大小、质地都相同的卡片,上面分别标有数字2,3,4(背面完全相同),现将标有数字的一面朝下.小明从中任意抽取一张,记下数字后放回洗匀,然后小亮从中任意抽取一张,计算小明和小亮抽得的两个数字之和.(1)、请你用画树状图或列表的方法,求出这两数和为6的概率.
(1)、当轿车刚到乙地时,此时货车距离乙地千米;(2)、当轿车与货车相遇时,求此时x的值;(3)、在两车行驶过程中,当轿车与货车相距20千米时,求x的值.22. 小明和小亮玩一个游戏:取三张大小、质地都相同的卡片,上面分别标有数字2,3,4(背面完全相同),现将标有数字的一面朝下.小明从中任意抽取一张,记下数字后放回洗匀,然后小亮从中任意抽取一张,计算小明和小亮抽得的两个数字之和.(1)、请你用画树状图或列表的方法,求出这两数和为6的概率.
(2)、如果和为奇数,则小明胜;若和为偶数,则小亮胜.你认为这个游戏规则对双方公平吗?做出判断,并说明理由.23. 如图,△ABC内接于⊙O,AB为直径,作OD⊥AB交AC于点D,延长BC,OD交于点F,过点C作⊙O的切线CE,交OF于点E.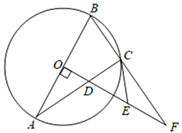 (1)、求证:EC=ED;(2)、如果OA=4,EF=3,求弦AC的长.24. 在平面直角坐标系中,已知抛物线L: 经过点A(-3,0)和点B(0,-6),L关于原点O对称的抛物线为 .
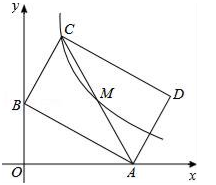
(1)、求证:EC=ED;(2)、如果OA=4,EF=3,求弦AC的长.24. 在平面直角坐标系中,已知抛物线L: 经过点A(-3,0)和点B(0,-6),L关于原点O对称的抛物线为 . (1)、求抛物线L的表达式;(2)、点P在抛物线 上,且位于第一象限,过点P作PD⊥y轴,垂足为D.若△POD与△AOB相似,求符合条件的点P的坐标.25. 如图,在直角坐标系中,长方形ABCD(每个内角都是90°)的顶点的坐标分别是A(0,m),B(n,0),(m>n>0),点E在AD上,AE=AB,点F在y轴上,OF=OB,BF的延长线与DA的延长线交于点M,EF与AB交于点N.
(1)、求抛物线L的表达式;(2)、点P在抛物线 上,且位于第一象限,过点P作PD⊥y轴,垂足为D.若△POD与△AOB相似,求符合条件的点P的坐标.25. 如图,在直角坐标系中,长方形ABCD(每个内角都是90°)的顶点的坐标分别是A(0,m),B(n,0),(m>n>0),点E在AD上,AE=AB,点F在y轴上,OF=OB,BF的延长线与DA的延长线交于点M,EF与AB交于点N. (1)、试求点E的坐标(用含m,n的式子表示);(2)、求证:AM=AN;(3)、若AB=CD=12cm,BC=20cm,动点P从B出发,以2cm/s的速度沿BC向C运动的同时,动点Q从C出发,以vcm/s的速度沿CD向D运动,是否存在这样的v值,使得△ABP与△PQC全等?若存在,请求出v值;若不存在,请说明理由.
(1)、试求点E的坐标(用含m,n的式子表示);(2)、求证:AM=AN;(3)、若AB=CD=12cm,BC=20cm,动点P从B出发,以2cm/s的速度沿BC向C运动的同时,动点Q从C出发,以vcm/s的速度沿CD向D运动,是否存在这样的v值,使得△ABP与△PQC全等?若存在,请求出v值;若不存在,请说明理由.