辽宁省抚顺市望花区2019年数学中考二模试卷
试卷更新日期：2020-03-10 类型：中考模拟
一、单选题
-
1. 一元二次方程（x﹣2）＝x（x﹣2）的解是（ ）A、x＝1 B、x＝2 C、x1＝2，x2＝0 D、x1＝1，x2＝22. 如图，抛物线顶点坐标是P（1，﹣3），则函数y随自变量x的增大而减小的x的取值范围是（ ）
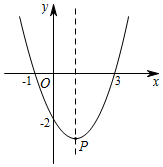A、x＞1 B、x＜1 C、x＞3 D、x＜33.如图，该图形围绕点O按下列角度旋转后，不能与其自身重合的是（ ）
A、72° B、108° C、144° D、216°4.如图，四边形ABCD是⊙O的内接四边形，∠B=70°，则∠D的度数是（ ）
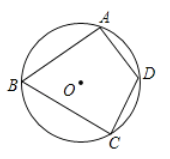A、110° B、90° C、70° D、50°5. 下列事件中，属于必然事件的是（ ）A、随意翻到一本书的某页，这页的页码是奇数 B、测量某天的最低气温，结果为﹣150℃ C、把4个球放到3个抽屉里，其中一个抽屉里至少有2个球 D、我市天气预报中说“明天降雪的概率是80%”，表示明天我市有80%的地区降雪6. 根据辽宁省人力资源和社会保障厅、辽宁省财政厅关于2018年调整退休人员基本养老金的通知文件精神，从2018年1月1日起，对我市企业退休人员基本养老金进行调整.已知企业退休职工李师傅2016年月退休金为2159元，2018年达到2394元.设李师傅的月退休金从2016年到2018年的年平均增长率为x，可列方程为（ ）A、2394（1﹣x）2＝2159 B、2159（1+x）2＝2394 C、2159（1﹣x）＝2394 D、2159+2159（1+x）+2159（1+x）2＝23947. 如图，一只花猫发现一只老鼠溜进了一个内部连通的鼠洞，鼠洞只有三个出口A，B，C，要想同时顾及这三个出口以防老鼠出洞，这只花猫最好蹲守在（ ）
A、△ABC的三边高线的交点处 B、△ABC的三角平分线的交点处 C、△ABC的三边中线的交点处 D、△ABC的三边中垂线的交点处8. 小明在一次用频率估计概率的实验中，统计了某一结果出现的频率，并绘制了如图所示的统计图，则符合这一结果的实验可能是（ ）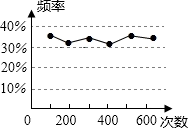
A、从一个装有2个白球和1个红球的不透明袋子中任意摸出一球（小球除颜色外，完全相同），摸到红球的概率 B、掷一枚质地均匀的硬币，正面朝上的概率 C、从一副去掉大小王的扑克牌，任意抽取一张，抽到黑桃的概率 D、任意买一张电影票，座位号是2的倍数的概率9.如图，A，B是半径为1的⊙O上两点，且OA⊥OB，点P从点A出发，在⊙O上以每秒一个单位长度的速度匀速运动，回到点A运动结束，设运动时间为x（单位：s），弦BP的长为y，那么下列图象中可能表示y与x函数关系的是（ ）
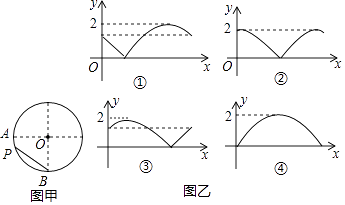A、① B、③ C、②或④ D、①或③10. 下列图形中，可以看作是中心对称图形的是（ ）A、
B、
C、
D、
二、填空题
-
11. 二次函数y＝（m﹣1）x2的图象开口向下，则m.12. 若关于x的一元二次方程x2﹣2x﹣k=0没有实数根，则k的取值范围是 ．
13. 如图，量角器的直径与直角三角板ABC的斜边AB重合，其中量角器0刻度线的端点N与点A重合，射线CP从CA处出发绕点C沿顺时针方向以每秒3度的速度旋转，CP与量角器的半圆弧交于点E，第10秒时，点E在量角器上对应的读数是度.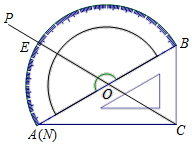
14. 要得到抛物线y＝ （x﹣4）2 ， 可将抛物线y＝ x2向平移4个单位.15. 已知点I是△ABC的内心，∠BIC＝130°，则∠BAC的度数是度.16. 如图，⊙O的半径为13，AB＝24，若点P在弦AB上运动，则OP的取值范围是.
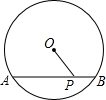17. 某航空公司有若干个飞机场，每两个飞机场之间都开辟一条航线，一共开辟了15条航线，则这个航空公司共有个飞机场.18. 如图，正六边形A1B1C1D1E1F1的边长为1，它的6条对角线围成一个正六边形A2B2C2D2E2F2；正六边形A2B2C2D2E2F2的6条对角线又围成一个正六边形A3B3C3D3E3F3…；如此继续下去，则六边形A4B4C4D4E4F4的面积是.
三、解答题
-
19. 先化简，再求值： ，其中x是一元二次方程x2+2x﹣3＝0的根.20. 抚顺市位于辽宁省东部，素有“煤都”之称，她不仅是清王朝的发祥地，还是中国最具幸福感城市，中国最具成长竞争力城市，《魅力中国城》“十佳魅力城市”，2018年9月28日上午，我们敬爱的习近平总书记亲自到抚顺市.小明所在的九年（3）班要召开一次“我可爱的家乡”主题班会活动，准备选取1名主持人及4名学生介绍抚顺风光.班主任准备了“①号一雷锋纪念馆”、“②号一赫图阿拉城”、“③号一清永陵”、“④号一高尔山”这四处景点的照片各一张，并将它们背面朝上放置（照片背面完全相同）.
(1)、已知九年（3）班共有48名同学，请写出小明被选中为主持人的概率；(2)、小明、小丽入选介绍抚顺风光.小明同学从四处景点的照片中随机抽取一张，不放回；小丽再从剩下的照片中随机抽取一张，若要根据抽取的照片作相关景点介绍，请用画树状图或列表法求小明、小丽两人中恰好有一人介绍“雷锋纪念馆”的概率.21. 如图，在平面直角坐标系中，A（﹣1，4），B（﹣4，0），C（﹣1，0）.
(1)、①△A1B1C1与△ABC关于原点O对称，画出△A1B1C1并写出点A1的坐标；②△A2B2C2是△ABC绕原点O顺时针旋转90°得到的，画出△A2B2C2并写出点A2的坐标；
(2)、连接OA、OA2 ， 在△ABC绕原点O顺时针旋转90°得到的△A2B2C2的过程中，计算线段OA变换到OA2过程中扫过区域的面积是多少？（直接写出答案）22. 如图，隧道的截面由抛物线和长方形构成，长方形OABC的长是12m，宽是4m，按照图中所示的平面直角坐标系，抛物线可以用y＝﹣ x2+2x+c表示.
(1)、请写出该抛物线的函数关系式；(2)、一辆货运汽车载一长方体集装箱后高为6m，宽为4m，如果隧道内设双向行车道，那么这辆货车能否安全通过？(3)、在抛物线形拱壁上需要安装两排灯，使它们离地面的高度相等.如果灯离地面的高度不超过8m，那么两排灯的水平距离最小是多少米？23. 如图，AB是⊙O的直径，BC交⊙O于点D，E是弧 的中点，AE与BC交于点F，∠C=2∠EAB.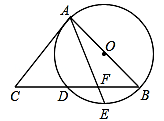
(1)、求证：AC是⊙O的切线；(2)、已知CD=4，CA=6，求AF的长.24. 某商店经销一种学生用双肩包，已知这种双肩包的成本价为每个30元.市场调查发现，这种双肩包每天的销售量y（个）与销售单价x（元）有如下关系：y=﹣x+60（30≤x≤60）.设这种双肩包每天的销售利润为w元.(1)、求w与x之间的函数关系式；(2)、这种双肩包销售单价定为多少元时，每天的销售利润最大？最大利润是多少元？(3)、如果物价部门规定这种双肩包的销售单价不高于42元，该商店销售这种双肩包每天要获得200元的销售利润，销售单价应定为多少.25. 已知△ABC是等边三角形，点P在射线AC上（点P与点A、点C不重合），点D在线段BC的延长线上，且AP＝CD，△PCD′与△PCD关于直线AC对称.
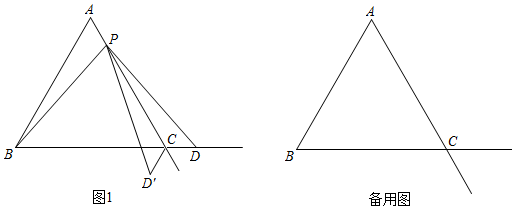(1)、如图1，当点P在线段AC上时，①求证：PB＝PD；
②请求出∠BPD′的度数；
(2)、当点P在射线AC上运动时，请直接回答：①PB＝PD是否仍然成立？
②∠BPD′的度数是否发生变化？
(3)、将△PCD′绕点P顺时针旋转，在旋转的过程中，PD′与PB能否重合？若能重合，请直接写出旋转的角度；若不能重合，请说明理由；(4)、若AB＝4，当点P为AC边的中点时，请直接写出PD'的长26. 如图1，在平面直角坐标系中，抛物线y＝﹣x2+bx+c与x轴分别交于A（﹣3，0），B两点，与y轴交于点C，点D为抛物线的顶点，抛物线的对称轴是x＝﹣1，且与x轴交于E点.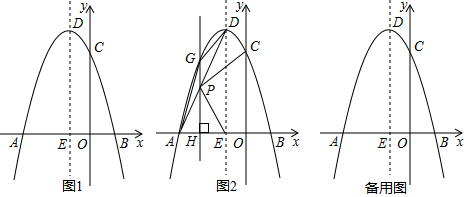
(1)、请直接写出抛物线的解析式及顶点D的坐标；(2)、如图2，连接AD，设点P是线段AD上的一个动点，过点P作x轴的垂线交抛物线于点G，交x轴于点H，连接AG、GD，当△ADG的面积为1时，①求点P的坐标；
②连接PC、PE，探究PC、PE的数量关系和位置关系，并说明理由；
(3)、设M为抛物线上一动点，N为抛物线的对称轴上一动点，Q为x轴上一动点，当以Q、M、N、E为顶点的四边形为正方形时，请直接写出点Q的坐标.