辽宁省大连市金普新区2019年数学中考二模试卷

试卷更新日期：2020-03-10 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列实数中，无理数是（）

A、0 B、－1 C、 $\sqrt{3}$ D、 $\frac{1}{3}$

查看试题解析
2.
如图是某一立体图形的三视图，则这个立体图形是（　　）

A、正三棱柱 B、三棱锥 C、圆柱 D、圆锥

查看试题解析
3. 在平面直角坐标系中，点 $P (- 3 ， 2)$ 所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 若点 $A (- 2, m)$ 在反比例函数 $y = \frac{2}{x}$ 的图象上，则 $m$ 的值是（）

A、 $\frac{1}{4}$ B、 $- \frac{1}{4}$ C、1 D、-1

查看试题解析
5. 如图，AB∥CD，∠A＝45°，∠C＝28°，则∠AEC的大小为（）

A、17° B、62° C、63° D、73°

查看试题解析
6. 将抛物线y＝x²向左平移2个单位，所得抛物线的解析式为（）

A、y＝x²﹣2 B、y＝x²+2 C、y＝（x+2）² D、y＝（x﹣2）²

查看试题解析
7. 如图，在菱形ABCD中，AB=5，对角线AC=6.若过点A作AE⊥BC，垂足为E，则AE的长为（）

A、4 B、2.4 C、4.8 D、5

查看试题解析
8. 小军旅行箱的密码是一个六位数，由于他忘记了密码的末位数字，则小军能一次打开该旅行箱的概率是（）

A、 $\frac{1}{10}$ B、 $\frac{1}{9}$ C、 $\frac{1}{6}$ D、 $\frac{1}{5}$

查看试题解析
9. 如果圆锥的底面半径为3，母线长为6，那么它的侧面积等于（）

A、9π B、18π C、24π D、36π

查看试题解析
10. 正方形ABCD、正方形BEFG，点A，B，E在半圆O的直径上，点D，C，F在半圆O上，若EF＝4，则该半圆的半径为（）

A、 $4 \sqrt{5}$ B、8 C、 $4 \sqrt{3}$ D、 $4 \sqrt{2}$

查看试题解析

二、填空题

11. 135万用科学记数法可表示为.

查看试题解析
12. 某区10名学生参加实际汉字听写大赛，他们得分情况如下表：

人数

3

4

2

1

分数

80

85

90

95

那么10名学生所得分数的中位数是.

查看试题解析
13. 若正n边形的内角和等于它的外角和，则边数n为.

查看试题解析
14. 某运输队只有大、小两种货车，已知1辆大车能运3吨货物，3辆小车能运1吨货物，100吨货物恰好由100辆车一次运完.设有x辆大车，y辆小车，根据题意可列方程组为.

查看试题解析
15. 在平面直角坐标系xOy中，A（1，1），B（3，1），双曲线y＝ $\frac{k}{x}$ 与线段AB有公共点，则k的取值范围是.

查看试题解析
16. 如图，△ABC内接于⊙O ， AB是⊙O直径，∠ACB的平分线交⊙O于D ，若AC＝m ， BC＝n ，则CD的长为（用含m、n的代数式表示）．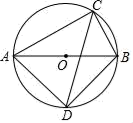

查看试题解析

三、解答题

17. 计算： $6 \sin 60^{0} - {(\frac{1}{3})}^{- 2} - \sqrt{12} + | 2 - \sqrt{3} |$ .

查看试题解析
18. 先化简，再求值：（1﹣ $\frac{b}{a + b}$ ）÷ $\frac{a}{a^{2} - b^{2}}$ ，其中a＝ $\sqrt{3}$ +1，b＝ $\sqrt{3}$ ﹣1.

查看试题解析
19. 如图，在四边形ABCD中，E是CB的中点，延长AE、DC相交于点F，∠CEA＝∠B+∠F.求证：AB＝FC.

查看试题解析

20. 某校为了解本校九年级男生“引体向上”项目的训练情况，随机抽取该年级部分男生进行了一次测试（满分15分，成绩均记为整数分），按测试成绩m（单位：分）分为A、B、C、D四个组别并绘制出以下两幅不完整的统计图，请根据图中信息解答下列问题：

分组	成绩	人数
A	12≤m≤15	10
B	9≤m≤11	22
C	6≤m≤8
D	m≤5	3

(1)、在被调查的男生中，成绩等级为D的男生有人，成绩等级为A的男生人数占被调查男生人数的百分比为%；

(2)、本次抽取样本容量为，成绩等级为C的男生有人；

(3)、若该校九年级男生有300名，估计成绩少于9分的男生人数.

查看试题解析

21. 某校其中九年级的3个班学生的捐款金额如下表：

吴老师统计时不小心把墨水滴到了其中两个班级的捐款金额上，但他知道下面三条信息：

信息一：这三个班的捐款总金额是7700元；

信息二：二班的捐款金额比三班的捐款金额多300元；

信息三：三班学生平均每人捐款的金额大于49元，小于50元.

请根据以上信息，帮助吴老师解决下列问题：

(1)、求出二班与三班的捐款金额各是多少元；

(2)、求出三班的学生人数.

查看试题解析
22. 甲、乙两人计划8：00一起从学校出发，乘坐班车去博物馆参观，乙乘坐班车准时出发，但甲临时有事，8：45才出发.甲沿相同的路线自行驾车前往，比乙早1小时到达.甲、乙两人离学校的距离y（千米）与甲出发时间x（小时）的函数关系如图所示.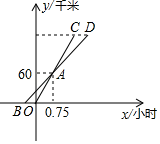

(1)、点A的实际意义：，点B坐标；CD＝；

(2)、学校与博物馆之间的距离.

查看试题解析
23. 如图，菱形ABCD，∠D＝60°，△ABC内接于⊙O，⊙O的直径AE交BC于F，DC的延长线交AE的延长线于点G.

(1)、求证：DG与⊙O相切；

(2)、连接DF，求tan∠FDC的值.

查看试题解析
24. 如图，在平面直角坐标系xOy中，矩形OABC的顶点A、C在坐标轴上，点A的坐标为(4，0).点C的坐标为(0，3).将矩形OABC绕点O逆时针旋转得到矩形OEFG，点B的对应点F恰好落在y轴正半轴上.将矩形OEFG沿y轴向下平移，当点E到达x轴上时，运动停止.设平移的距离为m，两矩形重叠面积为S.

(1)、求点E的坐标；

(2)、求S与m的函数关系式，并直接写出m的取值范围.

查看试题解析
25. 如图1，△ABC中，∠B＝30°，点D在BA的延长线上，点E在BC边上，连接DE，交AC于点F.若∠EFC＝60°，DE＝2AC，求 $\frac{AD}{BE}$ 的值.某学习小组的同学经过思考，交流了自己的想法：
小明：“通过观察和度量，发现∠C与∠D存在某种数量关系”；

小强：“通过构造三角形，证明三角形相似，进而可以求得 $\frac{AD}{BE}$ 的值.

老师：如图2，将原题中“点D在BA的延长线上，点E在BC边上”改为“点D在AB边上，点E在BC的延长线上”，添加条件“BC＝5 $\sqrt{3}$ ，EC＝4 $\sqrt{3}$ ”，其它条件不变，可求出△BED的面积.

请回答：

(1)、用等式表示∠C、∠D的数量关系并证明；

(2)、求 $\frac{AD}{BE}$ 的值；

(3)、△BDE的面积为（直接写出答案）.

查看试题解析
26. （定义）函数图象上的任意一点P（x，y），y﹣x称为该点的“坐标差”，函数图象上所有点的“坐标差”的最大值称为该函数的“特征值”
（感悟）根据你的阅读理解回答问题：

(1)、点P （2，1）的“坐标差”为；（直接写出答案）

(2)、求一次函数y＝2x+1（﹣2≤x≤3）的“特征值”；

(3)、（应用）二次函数y＝﹣x²+bx+c（bc≠0）交x轴于点A，交y轴于点B，点A与点B的“坐标差”相等，若此二次函数的“特征值”为﹣1，当m≤x≤m+3时，此函数的最大值为﹣2m，求m.

查看试题解析

人数	3	4	2	1
分数	80	85	90	95