湖北省武汉市2019年数学中考模拟试卷
试卷更新日期:2020-03-10 类型:中考模拟
一、单选题
-
1. ﹣10+3的结果是( )A、﹣7 B、7 C、﹣13 D、132. 下列分式中,无论x取何值,分式总有意义的是( )A、 B、 C、 D、3. 下列各组单项式中,为同类项的是( )A、a3与a2 B、a2与2a2 C、2xy与2x D、﹣3与a4. 在不透明袋子里装颜色不同的16个球,每次从袋子里摸出1个球记录下颜色后再放回,经过多次重复试验,发现摸到白球的频率稳定在0.5,估计袋中白球有( )A、16个 B、12个 C、8个 D、5个5. 若多项式 = ,则a,b的值分别是( )A、 , B、 , C、 , D、 ,6. 点P(4,-3)关于x轴对称的点的坐标是( )A、(4,3) B、(-4,-3) C、(-4,3) D、(-3,4)7. 如图所示几何体的左视图正确的是( )
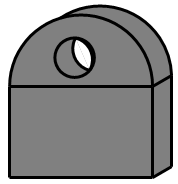 A、
A、 B、
B、 C、
C、 D、
D、 8. 组由正整数组成的数据:2、3、4、5、a、b,若这组数据的平均数为3,众数为2,则a为( )A、1 B、2 C、3 D、49. 已知 = =3, = =10, = =15,……观察以上计算过程,寻找规律.计算 C85=( )A、72 B、56 C、42 D、4010. 如图,⊙O内切于正方形ABCD,边AD,CD分别与⊙O切于点E,F,点M、N分别在线段DE,DF上,且MN与⊙O相切,若△MBN的面积为8,则⊙O的半径为( )
8. 组由正整数组成的数据:2、3、4、5、a、b,若这组数据的平均数为3,众数为2,则a为( )A、1 B、2 C、3 D、49. 已知 = =3, = =10, = =15,……观察以上计算过程,寻找规律.计算 C85=( )A、72 B、56 C、42 D、4010. 如图,⊙O内切于正方形ABCD,边AD,CD分别与⊙O切于点E,F,点M、N分别在线段DE,DF上,且MN与⊙O相切,若△MBN的面积为8,则⊙O的半径为( )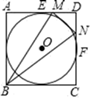 A、 B、2 C、 D、2
A、 B、2 C、 D、2二、填空题
-
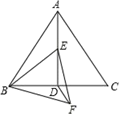
11. 计算: .12. 同时抛掷三枚质地均匀的硬币,出现两枚正面向下,一枚正面向上的概率是.13. 在 中, , ,连接 ,若 ,则线段 的长为.14. 如图,在边长为2的等边△ABC中,D是BC的中点,点E在线段AD上,连结BE , 在BE的下方作等边△BEF , 连结DF . 当△BDF的周长最小时,∠DBF的度数是 .
 15. 二次函数 的最大值是.
15. 二次函数 的最大值是.三、解答题
-
16. 计算: .17. 解方程组: .18. 如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上,求证:∠1=∠2.
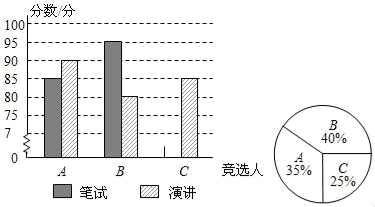
 19. 定安县定安中学初中部三名学生竞选校学生会主席,他们的笔试成绩和演讲成绩(单位:分)分别用两种方式进行统计,如表和图.
19. 定安县定安中学初中部三名学生竞选校学生会主席,他们的笔试成绩和演讲成绩(单位:分)分别用两种方式进行统计,如表和图.A
B
C
笔试
85
95
90
口试
80
85
 (1)、请将表和图中的空缺部分补充完整;(2)、图中B同学对应的扇形圆心角为度;(3)、竞选的最后一个程序是由初中部的300名学生进行投票,三名候选人的得票情况如图(没有弃权票,每名学生只能推荐一人),则A同学得票数为 , B同学得票数为 , C同学得票数为;(4)、若每票计1分,学校将笔试、演讲、得票三项得分按4:3:3的比例确定个人成绩,请计算三名候选人的最终成绩,并根据成绩判断当选.(从A,B,C选择一个填空)20. 某中学原计划加工一批校服,现有甲、乙两个工厂加工这批校服,已知甲工厂每天能加工这种校服16件,乙工厂每天加工这种校服24件,且单独加工这批校服甲厂比乙厂要多用20天(1)、求这批校服共有多少件?(2)、为了尽快完成这批校服,若先由甲、乙两工厂按原速度合作一段时间后,甲工厂停工,而乙工厂每天的速度提高25%,乙工厂单独完成剩下的部分,且乙工厂全部工作时间是甲工厂工作时间的2倍还多4天,求乙工厂加工多少天21. 如图,PA、PB是⊙O的切线,A,B为切点,D为⊙O上一点.
(1)、请将表和图中的空缺部分补充完整;(2)、图中B同学对应的扇形圆心角为度;(3)、竞选的最后一个程序是由初中部的300名学生进行投票,三名候选人的得票情况如图(没有弃权票,每名学生只能推荐一人),则A同学得票数为 , B同学得票数为 , C同学得票数为;(4)、若每票计1分,学校将笔试、演讲、得票三项得分按4:3:3的比例确定个人成绩,请计算三名候选人的最终成绩,并根据成绩判断当选.(从A,B,C选择一个填空)20. 某中学原计划加工一批校服,现有甲、乙两个工厂加工这批校服,已知甲工厂每天能加工这种校服16件,乙工厂每天加工这种校服24件,且单独加工这批校服甲厂比乙厂要多用20天(1)、求这批校服共有多少件?(2)、为了尽快完成这批校服,若先由甲、乙两工厂按原速度合作一段时间后,甲工厂停工,而乙工厂每天的速度提高25%,乙工厂单独完成剩下的部分,且乙工厂全部工作时间是甲工厂工作时间的2倍还多4天,求乙工厂加工多少天21. 如图,PA、PB是⊙O的切线,A,B为切点,D为⊙O上一点.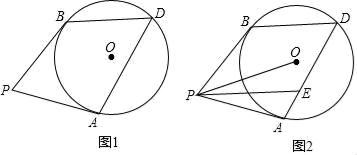 (1)、求证:∠P=180°﹣2∠D;(2)、如图,PE∥BD交AD于点E,若DE=2AE,tan∠OPE= ,⊙O的半径为2 ,求AE的长.22. 如图1,在平面直角坐标系xOy中,双曲线 与直线y=ax+b(a≠0)交于A、B两点,直线AB分别交x轴、y轴于C、D两点,E为x轴上一点.已知OA=OC=OE,A点坐标为(3,4).
(1)、求证:∠P=180°﹣2∠D;(2)、如图,PE∥BD交AD于点E,若DE=2AE,tan∠OPE= ,⊙O的半径为2 ,求AE的长.22. 如图1,在平面直角坐标系xOy中,双曲线 与直线y=ax+b(a≠0)交于A、B两点,直线AB分别交x轴、y轴于C、D两点,E为x轴上一点.已知OA=OC=OE,A点坐标为(3,4).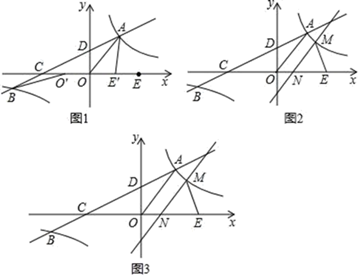 (1)、将线段OE沿x轴平移得线段O′E′(如图1),在移动过程中,是否存在某个位置使|BO′﹣AE′|的值最大?若存在,求出|BO′﹣AE′|的最大值及此时点O′的坐标;若不存在,请说明理由;(2)、将直线OA沿射线OE平移,平移过程中交 的图象于点M(M不与A重合),交x轴于点N(如图3).在平移过程中,是否存在某个位置使△MNE为以MN为腰的等腰三角形?若存在,求出M的坐标;若不存在,请说明理由.23. 如图,已知 和 ,点 在 边上, ,边 与 相交于点 .
(1)、将线段OE沿x轴平移得线段O′E′(如图1),在移动过程中,是否存在某个位置使|BO′﹣AE′|的值最大?若存在,求出|BO′﹣AE′|的最大值及此时点O′的坐标;若不存在,请说明理由;(2)、将直线OA沿射线OE平移,平移过程中交 的图象于点M(M不与A重合),交x轴于点N(如图3).在平移过程中,是否存在某个位置使△MNE为以MN为腰的等腰三角形?若存在,求出M的坐标;若不存在,请说明理由.23. 如图,已知 和 ,点 在 边上, ,边 与 相交于点 .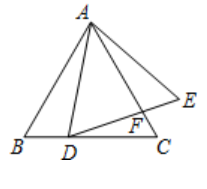 (1)、求证: ;(2)、如果 ,求证: .24. 如图,在平面直角坐标系中,抛物线y=ax2+bx﹣3交x轴于点A(﹣1,0)和点B(3,0),与y轴交于点C,顶点是D,对称轴交x轴于点E.
(1)、求证: ;(2)、如果 ,求证: .24. 如图,在平面直角坐标系中,抛物线y=ax2+bx﹣3交x轴于点A(﹣1,0)和点B(3,0),与y轴交于点C,顶点是D,对称轴交x轴于点E.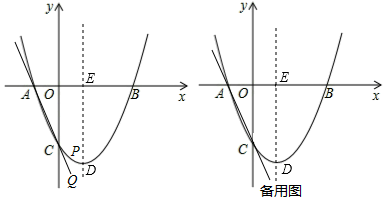 (1)、求抛物线的解析式;(2)、点P是抛物线在第四象限内的一点,过点P作PQ∥y轴,交直线AC于点Q,设点P的横坐标是m.
(1)、求抛物线的解析式;(2)、点P是抛物线在第四象限内的一点,过点P作PQ∥y轴,交直线AC于点Q,设点P的横坐标是m.①求线段PQ的长度n关于m的函数关系式;
②连接AP,CP,求当△ACP面积为 时点P的坐标;
(3)、若点N是抛物线对称轴上一点,则抛物线上是否存在点M,使得以点B,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出线段BN的长度;若不存在,请说明理由.