福建省福州市福清市2017-2018学年七年级下学期数学期中考试试卷

试卷更新日期：2020-03-09 类型：期中考试

进入出卷网下载

一、单选题

1. 3的平方根是（）

A、 $\sqrt{3}$ B、 $\pm 1.5$ C、9 D、 $\pm \sqrt{3}$

查看试题解析
2. 在下列所给出坐标的点中，在第二象限的是（）

A、 $(4, 3)$ B、 $(- 4, 3)$ C、 $(- 4, - 3)$ D、 $(4, - 3)$

查看试题解析
3. 在实数 $\sqrt{5}$ 、 $\sqrt{36}$ 、 $π$ 、0.1010010001……（1之间0依次增加1个）中，其中无理数一共有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 甲骨文是我国的一种古代文字，是汉字的早期形式，下列甲骨文中，不是轴对称的是（　　）

A、 B、 C、 D、

查看试题解析
5. 如图所示，下列说法错误的是（）

A、 $∠ 1$ 与 $∠ 2$ 是对顶角 B、 $∠ 1$ 与 $∠ 3$ 是同旁内角 C、 $∠ 1$ 与 $∠ 4$ 是内错角 D、 $∠ 2$ 与 $∠ 5$ 是同位角

查看试题解析
6. 下列命题中假命题是（）

A、在同一平面内，有三条直线 $a$ 、 $b$ 、 $c$ ，如果 $\vec{a} ⊥ \vec{b}$ ， $b ⊥ c$ ，则 $a ⊥ c$ B、当被开方数扩大到100倍时，算术平方根的结果扩大到10倍 C、在同一平面内，有三条直线 $a$ 、 $b$ 、 $c$ ，如果 $a ∥ b$ ， $b ∥ c$ ，则 $a ∥ c$ D、直线外一点到这条直线的垂线段的长度，叫做点到直线的距离

查看试题解析
7. 如图所示，点E在AB的延长线上，下列条件中不能判断AB//CD的是（）

A、∠1＝∠2 B、∠3＝∠4 C、∠C＝∠CBE D、∠C+∠ABC＝180°

查看试题解析
8. 如图，AB∥EF，CD⊥EF，∠BAC=50°，则∠ACD=（　　）

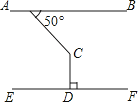A、120° B、130° C、140° D、150°

查看试题解析
9. 如图所示，在平面直角坐标系中，锐角三角形 $A B C$ 的三个顶点坐标分别是 $A (a ， b)$ 、 $B (c ， d)$ 、 $C (e ， d)$ ，在直线 $B C$ 上有四个点坐标分别是 $D (a - 1 ， d)$ 、 $E (a + 1 ， d)$ 、 $F (a ， d)$ 、 $G (e + 1 ， d)$ ，则点 $A$ 到直线 $B C$ 上的最短距离的点是（）

A、点 $D$ B、点 $E$ C、点 $F$ D、点 $G$

查看试题解析
10. 在平面直角坐标系中，有若干个横纵坐标分别为整数的点，其顺序按图中“→”方向排列，其对应的点坐标依次为 $(0， 0)$ ， $(1 ， 0)$ ， $(1 ， 1)$ ， $(0 ， 1)$ ， $(0 ， 2)$ ， $(1 ， 2)$ ， $(2 ， 2)$ ， $(2 ， 1)$ …，根据这个规律，第2018个横坐标为（）

A、44 B、45 C、46 D、47

查看试题解析

二、填空题

11. 命题“对顶角相等”改写成如果…那么…形式为

查看试题解析
12. 若点P在第四象限，且到x轴的距离3, 到y轴的距离4，则点P的坐标为.

查看试题解析
13. 如图，把一块三角板的直角的顶点放在直尺的一边上，若 $∠ 1 = 48 °$ ，则 $∠ 2 =$

查看试题解析
14. 在平面直角坐标系中，点 $A (- 1 + m ， 2 + m)$ 在 $x$ 轴上，则 $m =$

查看试题解析

15. 通过观察下列表格中的数据后再回答问题：

$a$	…	3.12	3.13	3.14	3.15	3.16	…
$a^{2}$	…	9.7344	9.7969	9.8596	9.9225	9.9856	…

根据乘方与开方互为逆运算的关系可知： $\sqrt{9.8}$ $π$ （填“ $<$ ”，“ $=$ ”，“ $>$ ”）

查看试题解析

16. 如图所示， $A D$ 与 $B C$ 被 $A B$ 所截，且 $A D ∥ B C$ ， $A C$ 平分 $∠ B A D$ ， $B D$ 平分 $∠ A B C$ ， $A C$ 与 $B D$ 相交于点 $F$ ，过点 $A$ 做 $A E ⊥ B C$ 于点 $E$ ，下列说法正确有（填上正确序号）

① $∠ B A C$ 与 $∠ A B D$ 互余；② $E A ⊥ A D$ ；③ $∠ A D B = ∠ A B D$ ；④ $A C \cdot B F = B C \cdot A E$

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt[3]{- 8} + \sqrt{16}$

(2)、 $\sqrt{2} (\sqrt{2} - 3) + | 1 - 3 \sqrt{2} |$

查看试题解析
18. 解方程或求值

(1)、 ${(x - 1)}^{2} = 1$

(2)、已知 $5 x - 2$ 的立方根是－3.求 $x + 69$ 的平方根.

查看试题解析
19. 完成下面的证明过程：
已知：如图 $A B ∥ C D$ ， $A D ∥ B E$ ， $∠ 3 = ∠ 4$ ，试说明 $∠ 1 = ∠ 2$ .

解：理由如下：

∵ $A B ∥ C D$ （已知），

∴ $∠ 4 =$ （），（理由：两直线平行，同位角相等）

∵（），

∴ $∠ 3 = ∠ D A C$ ，（理由：）

∵ $∠ 3 = ∠ 4$ ，（已知）

∴（），（等量代换）

∴ $∠ 1 + ∠ C A E =$ （） $+ ∠ C A E$ ，

∴ $∠ 1 = ∠ 2$ .

查看试题解析
20. 如图，直线 $A B$ ， $C D$ 相交于点 $O$ ， $O E$ 平分 $∠ B O C$ ， $O F ⊥ C D$ 于点 $O$ ， $∠ B O D ： ∠ E O B = 2 ： 3$ ，请补全图形，并求出 $∠ A O F$ 的度数.

查看试题解析
21. 如图所示的正方形网格中，每个小正方形的边长均为1个单位长度，三角形 $A B C$ 的三个顶点都在格点上.

(1)、请你以 $A$ 为原点 $O$ ，建立平面直角坐标系，并写出 $B$ 、 $C$ 两点的坐标.

(2)、若三角形 $A B C$ 内部有一点 $P (x ， y)$ ，经过平移后的对应点 $Q$ 的坐标为 $(x + 1 ， y - 2)$ ，且 $A$ 、 $B$ 、 $C$ 的对应点分别为 $D$ 、 $E$ 、 $F$ ，请说明三角形 $D E F$ 是如何由三角形 $A B C$ 平移得到（沿网格线平移），并画出三角形 $D E F$ .

查看试题解析
22. 命题：如果两条平行线被第三条直线所截，那么一组内错角的平分线互相平行，如图为符合该命题的示意图.

(1)、请你根据图形把该命题用几何符号语言补充完整，已知：直线 $A B$ 、 $C D$ 被第三条直线 $E F$ 所截，且 $A B ∥ C D$ ， $E M$ 平分 $∠ A E F$ ， $F N$ 平分，则 $∥$

(2)、判断该命题的真假，若是假命题，请举例说明：若是真命题，请证明.

查看试题解析
23. 在平面直角坐标系中， $Δ A B C$ 的顶点坐标分别为 $A (2 ， 0)$ ， $B (0 ， 4)$ ， $C (- 3 ， 2)$ .

(1)、求 $Δ A B C$ 的面积.

(2)、若 $A C$ 交 $y$ 轴于点 $D$ ，请求出 $D$ 点的坐标.

查看试题解析
24. 将如图1中的边长为1个单位长度的10个小正方形，沿 $B C$ 、 $B E$ 剪开，后把阴影部分补到如图2三角形 $C G H$ 与三角形 $E H F$ 位置中，拼成了一个大正方形，大正方形的边长设为 $a$ ；如图3将直径为1的圆放在点 $P$ 处， $P$ 对应的数位 $\sqrt{3}$ ，将圆周沿数轴向左边滚动一周到 $Q$ 点， $Q$ 对应数为 $b$ ，请完成下面问题：

(1)、求出 $a$ 与 $b$ 的值.

(2)、化简求值： $| a - 3 | + {(b + π)}^{2}$

查看试题解析
25. 如图1所示，在平面直角坐标系中， $A (a ， 0)$ 、 $B (0 ， b)$ 、 $C (1 ， - 3)$ ，其中 $a$ 、 $b$ 满足关系式 $\sqrt{a - 3} + {(a + b - 7)}^{2} = 0$ ，平移 $A C$ 使点 $A$ 与点 $B$ 重合，点 $C$ 的对应点为点 $D$ .

(1)、直接写出 $A$ 、 $D$ 两点的坐标，则 $A$ （，）、 $D$ （，）.

(2)、如图1，过点 $D$ 作 $D E ⊥ y$ 轴交于 $E$ 点，猜想 $∠ C A G$ 与 $∠ B D E$ 数量关系，并说明理由.

(3)、如图2，过点 $C$ 作 $C F ∥ x$ 轴交 $y$ 轴于 $F$ 点， $Q$ 为 $x$ 轴上点 $A$ 左侧的一动点，连接 $Q C$ ， $C M$ 平分 $∠ Q C A$ ， $C N$ 平分 $∠ F C A$ ，当点 $Q$ 运动时， $\frac{∠ M C N}{∠ A Q C}$ 的值是否变化？如果变化，请说明理由；如果不变，请求出其值.

查看试题解析