备考2020年中考数学二轮复习拔高训练卷3 函数的图象与性质
试卷更新日期:2020-03-07 类型:二轮复习
一、单选题
-
1. 函数y=ax2与y=ax+b(a>0,b>0)在同一坐标系中的大致图象是( )A、
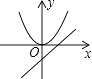 B、
B、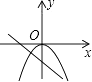 C、
C、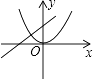 D、
D、 2. 如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB= ,反比例函数y= 在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )
2. 如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB= ,反比例函数y= 在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )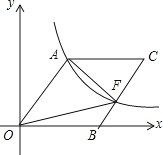 A、60 B、80 C、30 D、403.
A、60 B、80 C、30 D、403.如图,已知△ABC为等边三角形,AB=2,点D为边AB上一点,过点D作DE∥AC,交BC于E点;过E点作EF⊥DE,交AB的延长线于F点.设AD=x,△DEF的面积为y,则能大致反映y与x函数关系的图象是( )
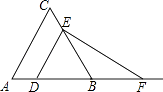 A、
A、 B、
B、 C、
C、 D、
D、 4. 如图,已知点 A 、B分别在反比例函数 的图象上,且OA ⊥OB ,则 的值为( )
4. 如图,已知点 A 、B分别在反比例函数 的图象上,且OA ⊥OB ,则 的值为( )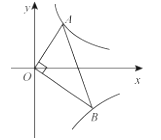 A、 B、2 C、 D、45. 如图,直线y=x+3交x轴于A点,将一块等腰直角三角形纸板的直角顶点置于原点O,另两个顶点M、N恰落在直线y=x+3上,若N点在第二象限内,则tan∠AON的值为( )
A、 B、2 C、 D、45. 如图,直线y=x+3交x轴于A点,将一块等腰直角三角形纸板的直角顶点置于原点O,另两个顶点M、N恰落在直线y=x+3上,若N点在第二象限内,则tan∠AON的值为( )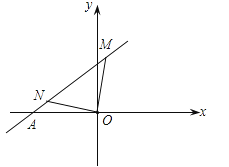 A、 B、 C、 D、6. 如图,边长为2的等边△ABC和边长为1的等边△A′B′C′,它们的边B′C′,BC位于同一条直线l上,开始时,点C′与B重合,△ABC固定不动,然后把△A′B′C′自左向右沿直线l平移,移出△ABC外(点B′与C重合)停止,设△A′B′C′平移的距离为x,两个三角形重合部分的面积为y,则y关于x的函数图象是( )
A、 B、 C、 D、6. 如图,边长为2的等边△ABC和边长为1的等边△A′B′C′,它们的边B′C′,BC位于同一条直线l上,开始时,点C′与B重合,△ABC固定不动,然后把△A′B′C′自左向右沿直线l平移,移出△ABC外(点B′与C重合)停止,设△A′B′C′平移的距离为x,两个三角形重合部分的面积为y,则y关于x的函数图象是( ) A、
A、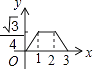 B、
B、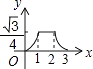 C、
C、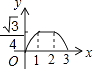 D、
D、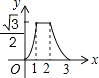 7. 如图,在矩形ABCD中,AB=2,AD=3,点E是BC边上靠近点B的三等分点,动点P从点A出发,沿路径A→D→C→E运动,则△APE的面积y与点P经过的路径长x之间的函数关系用图象表示大致是( )
7. 如图,在矩形ABCD中,AB=2,AD=3,点E是BC边上靠近点B的三等分点,动点P从点A出发,沿路径A→D→C→E运动,则△APE的面积y与点P经过的路径长x之间的函数关系用图象表示大致是( )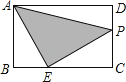 A、
A、 B、
B、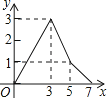 C、
C、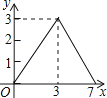 D、
D、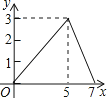 8. 如图1,在等边△ABC中,点E、D分别是AC,BC边的中点,点P为AB边上的一个动点,连接PE,PD,PC,DE.设AP=x,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( )
8. 如图1,在等边△ABC中,点E、D分别是AC,BC边的中点,点P为AB边上的一个动点,连接PE,PD,PC,DE.设AP=x,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( ) A、线段DE B、线段PD C、线段PC D、线段PE9. 甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.则下列结论:
A、线段DE B、线段PD C、线段PC D、线段PE9. 甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.则下列结论:①a=40,m=1;
②乙的速度是80km/h;
③甲比乙迟 h到达B地;
④乙车行驶 小时或 小时,两车恰好相距50km.
正确的个数是( )
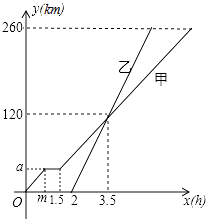 A、1 B、2 C、3 D、410. 正方形ABCD边长为1,E,F,G,H分别为边AB,BC,CD,DA上的点,且AE=BF=CG=DH.设小正方形EFGH的面积为y,AE=x. 则y关于x的函数图象大致是( )A、
A、1 B、2 C、3 D、410. 正方形ABCD边长为1,E,F,G,H分别为边AB,BC,CD,DA上的点,且AE=BF=CG=DH.设小正方形EFGH的面积为y,AE=x. 则y关于x的函数图象大致是( )A、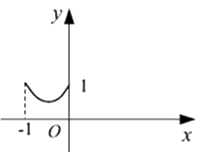 B、
B、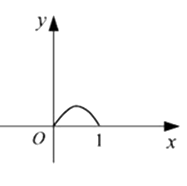 C、
C、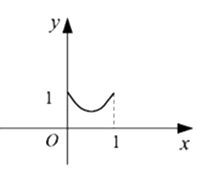 D、
D、 11. 如图,平行于x轴的直线与函数 (k1>0,x>0),y=(k2>0,x>0)的图像分别交于A,B两点,点A在点B的右侧,C为x轴上的一个动点.若△ABC的面积为4,则k1-k2的值为( )
11. 如图,平行于x轴的直线与函数 (k1>0,x>0),y=(k2>0,x>0)的图像分别交于A,B两点,点A在点B的右侧,C为x轴上的一个动点.若△ABC的面积为4,则k1-k2的值为( )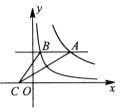 A、8 B、-8 C、4 D、-412. 如图,二次函数 的图象与 轴交于 两点,点 位于 、 之间,与 轴交于点 ,对称轴为直线 ,直线 与抛物线 交于 两点, 点在 轴上方且横坐标小于5,则下列结论:① ;② ;③ (其中 为任意实数);④ ,其中正确的是( )
A、8 B、-8 C、4 D、-412. 如图,二次函数 的图象与 轴交于 两点,点 位于 、 之间,与 轴交于点 ,对称轴为直线 ,直线 与抛物线 交于 两点, 点在 轴上方且横坐标小于5,则下列结论:① ;② ;③ (其中 为任意实数);④ ,其中正确的是( )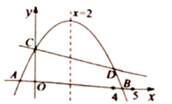 A、①②③④ B、①②③ C、①②④ D、①③④
A、①②③④ B、①②③ C、①②④ D、①③④二、填空题
-
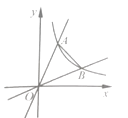
13. 如图,在平面直角坐标系中,反比例函数 (x>0)与正比例函数y=kx、 (k>1)的图像分别交于点A、B,若∠AOB=45°,则△AOB的面积是.
 14. 如图坐标系中,O(0,0),A(6,6 ),B(12,0),将△OAB沿直线线CD折叠,使点A恰好落在线段OB上的点E处,若OE= ,则CE:DE的值是 .
14. 如图坐标系中,O(0,0),A(6,6 ),B(12,0),将△OAB沿直线线CD折叠,使点A恰好落在线段OB上的点E处,若OE= ,则CE:DE的值是 .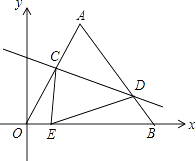 15. 如图,点 为直线 上的两点,过 两点分别作y轴的平行线交双曲线 ( )于 两点. 若 ,则 的值为.
15. 如图,点 为直线 上的两点,过 两点分别作y轴的平行线交双曲线 ( )于 两点. 若 ,则 的值为.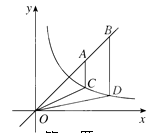 16. 如图,0为原点,A(4,0),E(0,3),四边形OABC,四边形OCDE都为平行四边形,OC=5,函数y= (x>0)的图象经过AB的中点F和DE的中点G,则k的值为 .
16. 如图,0为原点,A(4,0),E(0,3),四边形OABC,四边形OCDE都为平行四边形,OC=5,函数y= (x>0)的图象经过AB的中点F和DE的中点G,则k的值为 .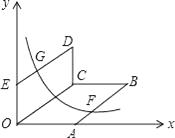 17. 已知反比例函数y= 的图象,当x取1,2,3,…n时,对应在反比例图象上的点分别为M1、M2、M3…Mn , 则 + +… = .
17. 已知反比例函数y= 的图象,当x取1,2,3,…n时,对应在反比例图象上的点分别为M1、M2、M3…Mn , 则 + +… = .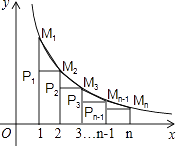
三、解答题
-
18. 如图1,抛物线 平移后过点A(8,0)和原点,顶点为B,对称轴与 轴相交于点C,与原抛物线相交于点D.
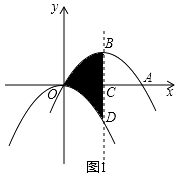
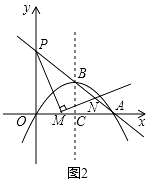
 (1)、求平移后抛物线的解析式并直接写出阴影部分的面积 ;(2)、如图2,直线AB与 轴相交于点P,点M为线段OA上一动点, 为直角,边MN与AP相交于点N,设 ,试探求:
(1)、求平移后抛物线的解析式并直接写出阴影部分的面积 ;(2)、如图2,直线AB与 轴相交于点P,点M为线段OA上一动点, 为直角,边MN与AP相交于点N,设 ,试探求:① 为何值时 为等腰三角形;
②
 为何值时线段PN的长度最小,最小长度是多少.19. 如图,抛物线 与 轴交于 、 两点(点 在点 的左侧),点 的坐标为 ,与 轴交于点 ,作直线 .动点 在 轴上运动,过点 作 轴,交抛物线于点 ,交直线 于点 ,设点 的横坐标为 .
为何值时线段PN的长度最小,最小长度是多少.19. 如图,抛物线 与 轴交于 、 两点(点 在点 的左侧),点 的坐标为 ,与 轴交于点 ,作直线 .动点 在 轴上运动,过点 作 轴,交抛物线于点 ,交直线 于点 ,设点 的横坐标为 .(Ⅰ)求抛物线的解析式和直线 的解析式;
(Ⅱ)当点 在线段 上运动时,求线段 的最大值;
(Ⅲ)当以 、 、 、 为顶点的四边形是平行四边形时,直接写出 的值.
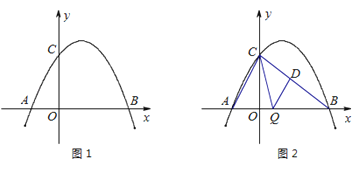
 20. 已知:二次函数y=ax2+bx+6(a≠0)与x轴交于A、B两点(点A在点B的左侧),点A、点B的横坐标是一元二次方程x2﹣4x﹣12=0的两个根.
20. 已知:二次函数y=ax2+bx+6(a≠0)与x轴交于A、B两点(点A在点B的左侧),点A、点B的横坐标是一元二次方程x2﹣4x﹣12=0的两个根.(1)请直接写出点A、点B的坐标.
(2)请求出该二次函数表达式及对称轴和顶点坐标.
(3)如图1,在二次函数对称轴上是否存在点P,使△APC的周长最小,若存在,请求出点P的坐标;若不存在,请说明理由.
(4)如图2,连接AC、BC,点Q是线段0B上一个动点(点Q不与点0、B重合).过点Q作QD∥AC交BC于点D,设Q点坐标(m,0),当△CDQ面积S最大时,求m的值.
 21. 已知平面直角坐标系中两定点A(﹣1,0)、B(4,0),抛物线y=ax2+bx﹣2(a≠0)过点A,B,顶点为C,点P(m,n)(n<0)为抛物线上一点.
21. 已知平面直角坐标系中两定点A(﹣1,0)、B(4,0),抛物线y=ax2+bx﹣2(a≠0)过点A,B,顶点为C,点P(m,n)(n<0)为抛物线上一点.
(1)、求抛物线的解析式和顶点C的坐标;
(2)、当∠APB为钝角时,求m的取值范围;
(3)、若m> ,当∠APB为直角时,将该抛物线向左或向右平移t(0<t< )个单位,点C、P平移后对应的点分别记为C′、P′,是否存在t,使得首位依次连接A、B、P′、C′所构成的多边形的周长最短?若存在,求t的值并说明抛物线平移的方向;若不存在,请说明理由.22. 如图,已知抛物线与x轴交于A(﹣1,0)、B(3,0)两点,与y轴交于点C(0,3).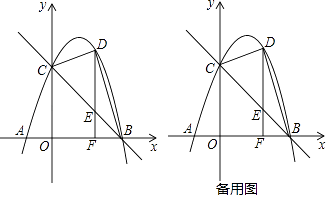 (1)、求抛物线的解析式.
(1)、求抛物线的解析式.
(2)、D是第一象限内抛物线上的一个动点(与点C、B不重合),过点D作DF⊥x轴于点F,交直线BC于点E,连结BD、CD设点D的横坐标为m,△BCD的面积为S.①求S关于m的函数关系式及自变量m的取值范围.
②当m为何值时,S有最大值,并求这个最大值.
23. 在平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是(0,4)、(﹣1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.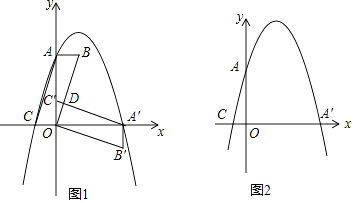 (1)、若抛物线经过点C、A、A′,求此抛物线的解析式;(2)、点M时第一象限内抛物线上的一动点,问:当点M在何处时,△AMA′的面积最大?最大面积是多少?并求出此时M的坐标;(3)、若P为抛物线上一动点,N为x轴上的一动点,点Q坐标为(1,0),当P、N、B、Q构成平行四边形时,求点P的坐标,当这个平行四边形为矩形时,求点N的坐标.24. 如图,在平面直角坐标系xOy中,矩形OABC的顶点B的坐标为(4,2),D是OA的中点,OE⊥CD交BC于点E,点P从点O出发,以每秒2个单位长度的速度沿射线OE运动.
(1)、若抛物线经过点C、A、A′,求此抛物线的解析式;(2)、点M时第一象限内抛物线上的一动点,问:当点M在何处时,△AMA′的面积最大?最大面积是多少?并求出此时M的坐标;(3)、若P为抛物线上一动点,N为x轴上的一动点,点Q坐标为(1,0),当P、N、B、Q构成平行四边形时,求点P的坐标,当这个平行四边形为矩形时,求点N的坐标.24. 如图,在平面直角坐标系xOy中,矩形OABC的顶点B的坐标为(4,2),D是OA的中点,OE⊥CD交BC于点E,点P从点O出发,以每秒2个单位长度的速度沿射线OE运动.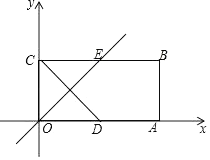 (1)、求直线OE的解析式;(2)、设以C,P,D,B为顶点的凸四边形的面积为S,点P的运动时间为t(单位:秒),求S关于t的函数解析式,并写出自变量t的取值范围;(3)、设点N为矩形的中心,则在点P运动过程中,是否存在点P,使以P,C,N为顶点的三角形是直角三角形?若存在,请直接写出t的值及点P的坐标;若不存在,请说明理由.25. 如图,已知抛物线的方程C1: (m>0)与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧.
(1)、求直线OE的解析式;(2)、设以C,P,D,B为顶点的凸四边形的面积为S,点P的运动时间为t(单位:秒),求S关于t的函数解析式,并写出自变量t的取值范围;(3)、设点N为矩形的中心,则在点P运动过程中,是否存在点P,使以P,C,N为顶点的三角形是直角三角形?若存在,请直接写出t的值及点P的坐标;若不存在,请说明理由.25. 如图,已知抛物线的方程C1: (m>0)与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧. (1)、若抛物线C1过点M(2, 2),求实数m的值;(2)、在(1)的条件下,在抛物线的对称轴上找一点H,使得BH+EH最小,求出点H的坐标;(3)、在第四象限内,抛物线C1上是否存在点F,使得以点B、C、F为顶点的三角形与△BCE相似?若存在,求m的值;若不存在,请说明理由.
(1)、若抛物线C1过点M(2, 2),求实数m的值;(2)、在(1)的条件下,在抛物线的对称轴上找一点H,使得BH+EH最小,求出点H的坐标;(3)、在第四象限内,抛物线C1上是否存在点F,使得以点B、C、F为顶点的三角形与△BCE相似?若存在,求m的值;若不存在,请说明理由.