初中数学浙教版七年级下册3.4 乘法公式-平方差公式及其运用同步训练

试卷更新日期：2020-03-06 类型：同步测试

进入出卷网下载

一、基础夯实

1. 下列各式中，能用平方差公式计算的是（）

A、(-a-b)(a+b) B、(-a-b)(a-b) C、(-a+b-c)(-a+b-c) D、(-a+b)(a-b)

查看试题解析
2. 下列多项式的乘法中，不能用平方差公式计算的是（）

A、 $(4 x - 3 y) (- 3 y - 4 x)$ B、 $(2 x^{2} - y^{2}) (2 x^{2} + y^{2})$ C、 $(a + b - c) (- c - b + a)$ D、 $(- x + y) (x - y)$

查看试题解析
3. 下列两个多项式相乘，不能用平方差公式的是（）

A、(-5a+2b)(5a+2b) B、(-5a+2b)(-5a-2b) C、(-5a-2b)(5a-2b) D、(5a+2b)(-5a-2b)

查看试题解析
4. 下列运算正确是（）

A、（x+3y）（x﹣3y）＝x²﹣3y² B、（x+3y）（x﹣3y）＝x²﹣9y² C、（﹣x+3y）（x﹣3y）＝﹣x²﹣9y² D、（﹣x﹣3y）（x+3y）＝x²﹣9y²

查看试题解析
5. 已知 $a + b = 2 ，$ 则 $a^{2} - b^{2} + 4 b$ 的值是（）

A、4 B、3 C、2 D、1

查看试题解析
6. 在边长为a的正方形中挖掉一个边长为b的小正方形（a>b），把余下的部分剪拼成一个矩形（如图），通过计算图形（阴影部分）的面积，验证了一个等式，则这个等式是（）

A、a²-b²=（a+b）（a-b） B、（a+b）²=a²+2ab+b² C、（a-b）²=a²-2ab+b² D、a²-ab=a（a-b）

查看试题解析
7. 如果 $(- 2 x - 3 y) \cdot m = 4 x^{2} - 9 y^{2}, 则 m$ 表示的式子为（）

A、 $- 2 x + 3 y$ B、 $2 x - 3 y$ C、 $- 2 x - 3 y$ D、 $2 x + 3 y$

查看试题解析
8. 如图，在边长为 a 的正方形上剪去一个边长为b 的小正方形( a > b )，把剩下的部分剪拼成一个梯形，分别计算这两个图形阴影部分的面积，由此可以验证的等式是（）

A、a² - b² = (a + b)(a - b) B、(a + b)² = a² + 2ab + b² C、(a - b)² = a² - 2ab + b² D、a² - ab = a(a - b)

查看试题解析
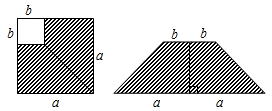9. 若（―x²―4y²)·A＝16y⁴―x⁴ ，则A＝ .

查看试题解析
10. 如图，边长为a的正方形中有一个边长为b的小正方形，若将图1的阴影部分拼成一个长方形，如图2，比较图1和图2的阴影部分的面积，你能得到的公式是.

查看试题解析
11. 计算：（ $\sqrt{3} + 2$ ）²⁰¹⁵（ $\sqrt{3} - 2$ ）²⁰¹⁶＝．

查看试题解析
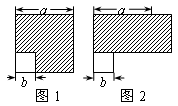12. 利用乘法公式计算：598×602

查看试题解析
13. 当n为自然数时，(n+7)²-(n-5)²能被24整除吗？说明理由．

查看试题解析

二、提高训练

14. 在幼发拉底河岸的古代庙宇图书馆遗址里，曾经发掘出大量的黏土板，美索不达米亚人在这些黏土板上刻出来乘法表、加法表和平方表.用这些简单的平方表，他们很快算出两数的乘积.例如：对于95×103，美索不达米亚人这样计算：第一步：（103+95）÷2=99；第二步：（103-95）÷2=4；第三步：查平方表，知99的平方是9801；第四步：查平方表，知4的平方是16；第五步：9801-16=9785=95×103. 请结合以上实例，设两因数分别为a和 b,写出蕴含其中道理的整式运算（）

A、 $\frac{{(a + b)}^{2} - {(a - b)}^{2}}{2} = a b$ B、 $\frac{{(a + b)}^{2} - (a^{2} + b^{2})}{2} = a b$ C、 ${(\frac{a + b}{2})}^{2} + {(\frac{a - b}{2})}^{2} = a b$ D、 ${(\frac{a + b}{2})}^{2} - {(\frac{a - b}{2})}^{2} = a b$

查看试题解析
15. 两个连续奇数的平方差是（）

A、16的倍数 B、8的倍数 C、12的倍数 D、6的倍数

查看试题解析
16. 观察下面的解题过程，然后化简：
（2+1）（2²+1）（2⁴+1）

＝（2﹣1）（2+1）（2²+1）（2⁴+1）

＝（2²﹣1）（2²+1）（2⁴+1）

＝（2⁴﹣1）（2⁴+1）

＝2⁸﹣1

化简：（3+1）（3²+1）（3⁴+1）（3⁸+1）＝．

查看试题解析
17.

(1)、计算下列各式，并寻找规律：
① $1 - \frac{1}{2^{2}}$ =（_+_）（_-_）=

② $1 - \frac{1}{3^{2}}$ =（_+_）（_-_）=_；

(2)、运用（1）中所发现的规，计算： $(1 - \frac{1}{2^{2}}) (1 - \frac{1}{3^{2}}) (1 - \frac{1}{4^{2}}) (1 - \frac{1}{5^{2}})$ ;

(3)、猜想 $(1 - \frac{1}{2^{2}}) (1 - \frac{1}{3^{2}}) (1 - \frac{1}{4^{2}}) \dots (1 - \frac{1}{9^{2}}) (1 - \frac{1}{10^{2}}) \dots (1 - \frac{1}{n^{2}})$ 的结果，并写出推理过程.

查看试题解析

初中数学浙教版七年级下册3.4 乘法公式-平方差公式及其运用 同步训练

一、基础夯实

二、提高训练

初中数学浙教版七年级下册3.4 乘法公式-平方差公式及其运用同步训练