初中数学浙教版七年级下册3.3 多项式的乘法同步训练

试卷更新日期：2020-03-06 类型：同步测试

进入出卷网下载

一、基础巩固

1. 要使多项式(x²－px＋2)(x－q)不含x的二次项，则p与q的关系是（）

A、相等 B、互为相反数 C、互为倒数 D、乘积为－1

查看试题解析
2. 如果二次三项式 $x^{2} + a x + 2$ 可分解为 $(x - 1) (x + b)$ ，则 $a + b$ 的值为（）

A、 $- 2$ B、 $- 5$ C、3 D、5

查看试题解析
3. 若 $(x^{2} - p x + q) (x - 3)$ 展开后不含 $x$ 的一次项，则 $p$ 与 $q$ 的关系是（）

A、 $p = 3 q$ B、 $q + 3 p = 0$ C、 $p + 3 q = 0$ D、 $q = 3 p$

查看试题解析
4. 若 $(x - 1) (x + 3) = x^{2} + a x + b$ ，则a，b的值分别为（　　　　）

A、a=2，b=3 B、a=﹣2，b=﹣3 C、a=﹣2，b=3 D、a=2，b=﹣3

查看试题解析
5. 计算（2x-3）（3x+4）的结果，与下列哪一个式子相同？（）

A、 $- 7 x + 4$ B、 $- 7 x - 12$ C、 $6 x^{2} - 12$ D、 $6 x^{2} - x - 12$

查看试题解析
6. 计算(x－1)(x－2)的结果为（）

A、x²＋2 B、x²－3x＋2 C、x²－3x－3 D、x²－2x＋2

查看试题解析
7. 随着数学学习的深入，数系不断扩充，引入新数 $i$ ，规定 $i^{2} = - 1$ ，并且新数 $i$ 满足交换律、结合律和分配律，则 $(1 + i) \cdot (2 - i)$ 运算结果是（）

A、 $3 - i$ B、 $2 + i$ C、 $1 - i$ D、 $3 + i$

查看试题解析
8. 已知三角形的底边是 $(6 a + 2 b)$ cm，高是 $(2 b - 3 a)$ cm，则这个三角形的面积是 cm $^{2}$ ．

查看试题解析
9. 若多项式A满足， $A \cdot (- a + 1) = a^{2} - 1$ ，则A=.

查看试题解析
10. 若化简（x+1）（2x+m）的结果中x的一次项系数是-5，则数m的值为.

查看试题解析
11. 计算：

(1)、（3x-1）（2x²+3x-4）

(2)、（x+2y）（x²-2xy+4y²）.

查看试题解析
12. 若(x² +mx－8)(x²－3x+n)的展开式中不含 x²和 x³项，求 m和 n的值.

查看试题解析

二、提高训练

13. 小思同学用如图所示的A，B，C三类卡片若干张，拼出了一个长为2a＋b、宽为a＋b的长方形图形.请你通过计算求出小思同学拼这个长方形所用A，B，C三类卡片各（）张.

A、2张，1张，2张 B、3张，2张，1张 C、2张，1张，1张 D、3张，1张，2张

查看试题解析
14. 若2x³﹣ax²﹣5x+5＝（2x²+ax﹣1）（x﹣b）+3，其中a ， b为整数，则ab的值为（）

A、2 B、﹣2 C、4 D、﹣4

查看试题解析
15. 观察下列两个多项式相乘的运算过程：

根据你发现的规律，若（x+a）（x+b）=x²-7x+12，则a ， b的值可能分别是（）

A、 $- 3$ ， $- 4$ B、 $- 3$ ，4 C、3， $- 4$ D、3，4

查看试题解析
16. 如果一个一次二项式与(x²-2x-1)的积所得的多项式中不含一次项，那么这个一次二项式可以是（只要写出一个符合条件的多项式）．

查看试题解析
17. 先阅读再解答：我们已经知道，根据几何图形的面积关系可以说明完全平方公式，实际上还有一些等式也可以用这种方式加以说明，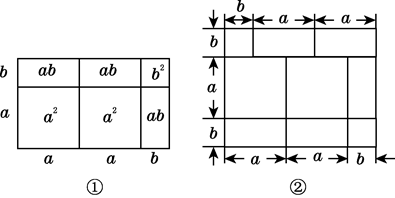

例如：

(2a＋b)(a＋b)＝2a²＋3ab＋b² ，就可以用图①的面积关系来说明．

(1)、根据图②写出一个等式：；

(2)、已知等式：(x＋p)(x＋q)＝x²＋(p＋q)x＋pq，请你画出一个相应的几何图形加以说明．

查看试题解析
18. 阅读材料
小明遇到这样一个问题：求计算 $(x + 2) (2 x + 3) (3 x + 4)$ 所得多项式的一次项系数.

小明想通过计算 $(x + 2) (2 x + 3) (3 x + 4)$ 所得的多项式解决上面的问题，但感觉有些繁琐，他想探寻一下，是否有相对简洁的方法.

他决定从简单情况开始，先找 $(x + 2) (2 x + 3)$ 所得多项式中的一次项系数，通过观察发现：

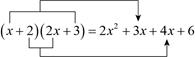
也就是说，只需用 $x + 2$ 中的一次项系数1乘以 $2 x + 3$ 中的常数项3，再用 $x + 2$ 中的常数项2乘以 $2 x + 3$ 中的一次项系数2，两个积相加 $1 \times 3 + 2 \times 2 = 7$ ，即可得到一次项系数.

延续上面的方法，求计算 $(x + 2) (2 x + 3) (3 x + 4)$ 所得多项式的一次项系数，可以先用 $x + 2$ 的一次项系数1， $2 x + 3$ 的常数项3， $3 x + 4$ 的常数项4，相乘得到12；再用 $2 x + 3$ 的一次项系数2， $x + 2$ 的常数项2， $3 x + 4$ 的常数项4，相乘得到16；然后用 $3 x + 4$ 的一次项系数3， $x + 2$ 的常数项2 $2 x + 3$ 的常数项3，相乘得到18.最后将12，16，18相加，得到的一次项系数为46.

参考小明思考问题的方法，解决下列问题：

(1)、计算 $(x + 4) (4 x + 3)$ 所得多项式的一次项系数为.

(2)、计算 $(x + 1) (3 x - 2) (2 x + 5)$ 所得多项式的一次项系数为.

(3)、若 $x^{2} - 3 x + 1$ 是 $x^{4} + a x^{2} + b x + 2$ 的一个因式，求 $a$ 、 $b$ 的值.

查看试题解析

初中数学浙教版七年级下册3.3 多项式的乘法 同步训练

一、基础巩固

二、提高训练

初中数学浙教版七年级下册3.3 多项式的乘法同步训练