备考2020年中考数学二轮复习拔高训练卷 专题2 方程与不等式
试卷更新日期:2020-03-05 类型:二轮复习
一、单选题
-
1. 下列方程中变形正确的是( )
① 4x+8=0变形为x+2=0; ② x+6=5-2x变形为3x=-1;
③ =3变形为4x=15; ④ 4x=2变形为x=2A、①④ B、①②③ C、③④ D、①②④2. 已知关于x的方程有且仅有两个不相等的实根,则实数a的取值范围为( )A、 B、 C、或 D、或3. 关于x的一元二次方程 有两个整数根且乘积为正,关于y的一元二次方程 同样也有两个整数根且乘积为正.给出四个结论:①这两个方程的根都是负根;② ;③ .其中正确结论的个数是( )
A、0个 B、1个 C、2个 D、3个4. 方程x2+ax+1=0和x2-x-a=0有一个公共根,则a的值是( )A、0 B、1 C、2 D、35. 若a为方程(x- )2=100的一根,b为方程(y-4)2=17的一根,且a、b都是正数,则a-b之值是( ). A、5 B、6 C、 D、10-
)2=100的一根,b为方程(y-4)2=17的一根,且a、b都是正数,则a-b之值是( ). A、5 B、6 C、 D、10- 6. 已知关于x的一元二次方程x2+ax+b=0有一个非零根-b , 则a-b的值为( )A、1 B、-1 C、0 D、-27. 方程x2-2x+3=0的根的情况是( ).A、有两个相等的实数根 B、只有一个实数根 C、没有实数根 D、有两个不相等的实数根8. 为了改善居民住房条件,某市计划用未来两年的时间,将城镇居民的住房面积由现在的人均约为20平方米提高到28.8平方米.若每年的年增长率相同,则年增长率为( )A、20% B、10% C、2% D、0.2%9. 已知⊙O与直线AB相交,且圆心O到直线AB的距离是方程2x-1=4的根,则⊙O的半径可为( ).A、1 B、2 C、2.5 D、310. 若数a使关于x的不等式组 有且仅有四个整数解,且使关于y的分式方程 + =2有非负数解,则所有满足条件的整数a的值之和是( )
6. 已知关于x的一元二次方程x2+ax+b=0有一个非零根-b , 则a-b的值为( )A、1 B、-1 C、0 D、-27. 方程x2-2x+3=0的根的情况是( ).A、有两个相等的实数根 B、只有一个实数根 C、没有实数根 D、有两个不相等的实数根8. 为了改善居民住房条件,某市计划用未来两年的时间,将城镇居民的住房面积由现在的人均约为20平方米提高到28.8平方米.若每年的年增长率相同,则年增长率为( )A、20% B、10% C、2% D、0.2%9. 已知⊙O与直线AB相交,且圆心O到直线AB的距离是方程2x-1=4的根,则⊙O的半径可为( ).A、1 B、2 C、2.5 D、310. 若数a使关于x的不等式组 有且仅有四个整数解,且使关于y的分式方程 + =2有非负数解,则所有满足条件的整数a的值之和是( )
A、3 B、1 C、0 D、﹣3二、填空题
-
11. 关于x的分式方程 的解为正数,则m的取值范围是 .12. 有甲、乙、丙3种商品,某人若购甲3件、乙7件、丙1件共需24元;若购甲4件、乙10件、丙1件共需33元,则此人购甲、乙、丙各一件共需 元。
13. 方程x2-2|x+4|-27=0的所有根的和为 .14. △ABC的两边长分别为2和3,第三边的长是方程x2-8x+15=0的根,则△ABC的周长是 .15. 若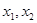 是方程 的两个实数根,且
是方程 的两个实数根,且 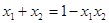 ,则 的值为.
,则 的值为.
三、计算题
-
16. 解方程组或不等式组:(1)、解方程组 ;(2)、解不等式组:17. 解下列方程:(1)、(x-5)2=x-5(2)、x2+12x+27=0(配方法).
四、解答题
-
18. 当x的取值范围是不等式组 的解时,试化简: .19. 关于x的方程 有两个不相等的实数根.(1)、求实数k的取值范围;(2)、设方程的两个实数根分别为 、 ,存不存在这样的实数k,使得 ?若存在,求出这样的k值;若不存在,说明理由.20. “母亲节”前夕,某商店根据市场调查,用3000元购进第一批盒装花,上市后很快售完,接着又用5000元购进第二批这种盒装花.已知第二批所购花的盒数是第一批所购花盒数的2倍,且每盒花的进价比第一批的进价少5元.求第一批盒装花每盒的进价是多少元?
五、综合题
-
21. 要运送一批货物,若用3台大货车各运7次,结果还有12件货物未运送完;若9台小货车各运4次,结果刚好运送完.已知每台大货车比每台小货车一次多运送3件货物.(1)、求这批货物共有多少件?(2)、已知每台大货车每次的运送费用为60元,每台小货车每次的运送费用为40元,若要想两次将所有货物运送完、(每台货车都运送3次,每次都是满载货物),问如何租用这两种货车,才合算呢?
22. 我县某包装生产企业承接了一批上海世博会的礼品盒制作业务,为了确保质量,该企业进行试生产.他们购得规格是170cm×40cm的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下A型与B型两种板材.如图1所示,(单位:cm)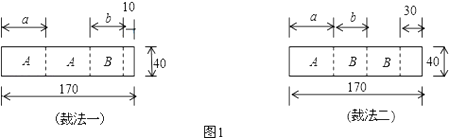 (1)、列出方程(组),求出图甲中a与b的值.(2)、在试生产阶段,若将30张标准板材用裁法一裁剪,4张标准板材用裁法二裁剪,再将得到的A型与B型板材做侧面和底面,做成图2的竖式与横式两种无盖礼品盒.
(1)、列出方程(组),求出图甲中a与b的值.(2)、在试生产阶段,若将30张标准板材用裁法一裁剪,4张标准板材用裁法二裁剪,再将得到的A型与B型板材做侧面和底面,做成图2的竖式与横式两种无盖礼品盒.①两种裁法共产生A型板材张,B型板材张;
②设做成的竖式无盖礼品盒x个,横式无盖礼品盒的y个,根据题意完成表格:
礼品盒板 材
竖式无盖(个)
横式无盖(个)
x
y
A型(张)
4x
3y
B型(张)
x

③做成的竖式和横式两种无盖礼品盒总数最多是个;此时,横式无盖礼品盒可以做个.(在横线上直接写出答案,无需书写过程)
23. 某通讯公司推出了移动电话的两种计费方式(详情见下表).月使用费/元
主叫限定时间/分
主叫超时费/(元/分)
被叫
方式一
58
150
0.25
免费
方式二
88
350
0.19
免费

设一个月内使用移动电话主叫的时间为t分(t为正整数),请根据表中提供的信息回答下列问题:
(1)、用含有t的式子填写下表:t≤150
150<t<350
t=350
t>350
方式一计费/元
58
108
方式二计费/元
88
88
88
(2)、当t为何值时,两种计费方式的费用相等?(3)、当330<t<360时,你认为选用哪种计费方式省钱(直接写出结果即可).24. 某公交公司有A,B型两种客车,它们的载客量和租金如下表:A
B
载客量(人/辆)
45
30
租金(元/辆)
400
280
学校根据实际情况,计划租用A、B型客车共5辆,同时送八年级师生到素质基地参加社会实践活动,设租用A型客车x辆,根据要求回答下列问题:
(1)、用含x的式子填写下表:车辆数(辆)
载客量
租金(元)
A
x
45x
400x
B
5-x
(2)、若要保证租车费用不超过1900元,求最多租用A型客车多少辆?(3)、在(2)的条件下,若八年级师生共有195人,写出所有可能的租车方案,并确定最省钱的租车方案。
25. 学校捐资购买了一批物资120吨打算支援山区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)车型
甲
乙
丙
汽车运载量(吨/辆)
5
8
10
汽车运费(元/辆)
400
500
600
(1)、若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?(2)、为了节省运费,该公司打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能分别求出三种车型的辆数吗?此时的运费又是多少元?