四川省成都市树德中2018-2019学年九年级上学期数学期中考试试卷
试卷更新日期:2020-03-05 类型:期中考试
一、单选题
-
1. 2018的相反数是( )A、 B、2018 C、-2018 D、2. 下列运算正确是( )A、 B、 C、 D、3. 小时候我们用肥皂水吹泡泡,其泡沫的厚度约0.000326毫米,用科学记数法表示为( )A、3.26×10﹣4毫米 B、0.326×10﹣4毫米 C、3.26×10﹣4厘米 D、32.6×10﹣4厘米4. 一元二次方程 的根的情况是A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根5. 已知函数y= ,则自变量x的取值范围是( )A、﹣1<x<1 B、x≥﹣1且x≠1 C、x≥﹣1 D、x≠16. 要调查安顺市中学生了解禁毒知识的情况,下列抽样调查最适合的是( )A、在某中学抽取200名女生 B、在安顺市中学生中抽取200名学生 C、在某中学抽取200名学生 D、在安顺市中学生中抽取200名男生7. 如图,在 中,斜边 , ,则直角边BC的长为
 A、 B、 C、 D、8. 一元二次方程x2﹣2x=0的两根分别为x1和x2 , 则x1x2为( )A、﹣2 B、1 C、2 D、09. 如图,在△ABC中,D,E分别是边AB,AC上的点,DE∥BC,AD:DB=2:1,下列结论中错误的是( )
A、 B、 C、 D、8. 一元二次方程x2﹣2x=0的两根分别为x1和x2 , 则x1x2为( )A、﹣2 B、1 C、2 D、09. 如图,在△ABC中,D,E分别是边AB,AC上的点,DE∥BC,AD:DB=2:1,下列结论中错误的是( ) A、 B、 C、 D、AD•AB=AE•AC10. 函数y=mx+n与
A、 B、 C、 D、AD•AB=AE•AC10. 函数y=mx+n与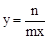 ,其中m≠0,n≠0,那么它们在同一坐标系中的图象可能是( )
,其中m≠0,n≠0,那么它们在同一坐标系中的图象可能是( )
A、 B、
B、 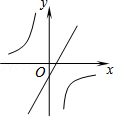 C、
C、 D、
D、
二、填空题
-
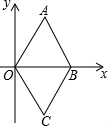
11. 分解因式: .12. 如图,在菱形OABC中,点B在x轴上,点A的坐标为 ,则点C的坐标为 .
 13. 如图:M为反比例函数 图象上一点, 轴于A, 时, .
13. 如图:M为反比例函数 图象上一点, 轴于A, 时, . 14. 如图,将 绕点A逆时针旋转 ,得到 ,这时点B、C、D恰好在同一直线上,则 的度数为 .
14. 如图,将 绕点A逆时针旋转 ,得到 ,这时点B、C、D恰好在同一直线上,则 的度数为 . 15. 实数a在数轴上的位置如图,化简 .
15. 实数a在数轴上的位置如图,化简 . 16. 关于x的一元二次方程 的两个实数根分别为 , ,且 ,则k的值是 .17. 如图,直线 ,且相邻两条平行线的距离都相等,若等腰 的三个顶点都在直线上,则 .
16. 关于x的一元二次方程 的两个实数根分别为 , ,且 ,则k的值是 .17. 如图,直线 ,且相邻两条平行线的距离都相等,若等腰 的三个顶点都在直线上,则 . 18. 如图,在平面直角坐标系中,直角梯形OABC的边OA,OC分别在x轴和y轴上,反比例函数 的图象经过AB的中点D,和BC相交于点E,连接OE,OD,DE,若 ,则 .
18. 如图,在平面直角坐标系中,直角梯形OABC的边OA,OC分别在x轴和y轴上,反比例函数 的图象经过AB的中点D,和BC相交于点E,连接OE,OD,DE,若 ,则 . 19. 如图,在正方形ABCD中,点E是BC边上一动点,连接AE,AC,将 沿AE翻折得到 ,延长 交CD边于F,若 ,则 用含n的代数式表示 .
19. 如图,在正方形ABCD中,点E是BC边上一动点,连接AE,AC,将 沿AE翻折得到 ,延长 交CD边于F,若 ,则 用含n的代数式表示 .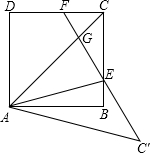
三、解答题
-
20. 先化简,再求值: ,其中x= .21. 为提升学生的艺术素养,学校计划开设四门艺术选修课:A.书法;B.绘画;C.乐器;D.舞蹈.为了解学生对四门功课的喜欢情况,在全校范围内随机抽取若干名学生进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).将数据进行整理,并绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:
 (1)、本次调查的学生共有多少人?扇形统计图中∠α的度数是多少?(2)、请把条形统计图补充完整;(3)、学校为举办2018年度校园文化艺术节,决定从A.书法;B.绘画;C.乐器;D.舞蹈四项艺术形式中选择其中两项组成一个新的节目形式,请用列表法或树状图求出选中书法与乐器组合在一起的概率.22. 如图,在一笔直的海岸线l上有A、B两个观测站, ,从A测得船C在北偏东 的方向,从B测得船C在北偏东 的方向.
(1)、本次调查的学生共有多少人?扇形统计图中∠α的度数是多少?(2)、请把条形统计图补充完整;(3)、学校为举办2018年度校园文化艺术节,决定从A.书法;B.绘画;C.乐器;D.舞蹈四项艺术形式中选择其中两项组成一个新的节目形式,请用列表法或树状图求出选中书法与乐器组合在一起的概率.22. 如图,在一笔直的海岸线l上有A、B两个观测站, ,从A测得船C在北偏东 的方向,从B测得船C在北偏东 的方向.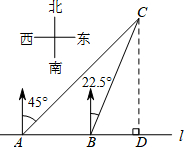 (1)、求 的度数;(2)、船C离海岸线l的距离 即CD的长 为多少? 不取近似值23. 如图,一次函数 的图象与反比例函数 的图象交于A,B两点,已知 , ,点B的坐标为
(1)、求 的度数;(2)、船C离海岸线l的距离 即CD的长 为多少? 不取近似值23. 如图,一次函数 的图象与反比例函数 的图象交于A,B两点,已知 , ,点B的坐标为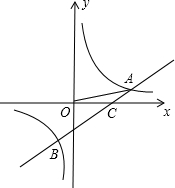 (1)、求反比例函数的解析式和一次函数的解析式;(2)、观察图象,直接写出使函数值 成立的自变量x的取值范围.24. 利民商店经销甲、乙两种商品 现有如下信息
(1)、求反比例函数的解析式和一次函数的解析式;(2)、观察图象,直接写出使函数值 成立的自变量x的取值范围.24. 利民商店经销甲、乙两种商品 现有如下信息信息1:甲乙两种商品的进货单价和为11;
信息2:甲商品的零售单价比其进货单价多2元,乙商品的零售单价比其进货单价的2倍少4元:
信息3:按零售单价购买甲商品3件和乙商品2件共付37元.
(1)、甲、乙两种商品的进货单价各是多少?(2)、据统计该商店平均每天卖出甲商品500件,经调查发现,甲商品零售单价每降 元,这样甲商品每天可多销售100件,为了使每天获取更大的利润,商店决定把甲种商品的零售单价下降a元,在不考虑其他因素的条件下,当a定为多少时,才能使商店每天销售甲种商品获取利润为1500元?25. 如图,在 中, , ,点D为AB延长线上一点,连接CD,过A分别作 ,垂足为M,交BC于点N,作 ,垂足为P,交CD于点Q. (1)、求证: ;(2)、如图,点E在BA的延长线上,且 ,连接EN并延长交CD于点F,求证: ;(3)、在(2)的条件下,当 时,请直接写出 的值为 .26. 有这样一个问题:探究同一坐标系中系数互为倒数的正、反比例函数 与 的图象性质 小明根据学习函数的经验,对这两个函数当 时的图象性质进行了探究 设函数 与 图象的交点为A、
(1)、求证: ;(2)、如图,点E在BA的延长线上,且 ,连接EN并延长交CD于点F,求证: ;(3)、在(2)的条件下,当 时,请直接写出 的值为 .26. 有这样一个问题:探究同一坐标系中系数互为倒数的正、反比例函数 与 的图象性质 小明根据学习函数的经验,对这两个函数当 时的图象性质进行了探究 设函数 与 图象的交点为A、下面是小明的探究过程:
(1)、如图所示,若已知A的坐标为 ,则B点的坐标为 . (2)、若A的坐标为 ,P点为第一象限内双曲线上不同于点B的任意一点.
(2)、若A的坐标为 ,P点为第一象限内双曲线上不同于点B的任意一点.①设直线PA交x轴于点M,直线PB交x轴于点 求证: .
证明过程如下:设 ,直线PA的解析式为 .
则
解得
所以,直线PA的解析式为 .
请把上面的解答过程补充完整,并完成剩余的证明.
②当P点坐标为 时,判断 的形状,并用k表示出 的面积.