四川省简阳市简城学区、镇金学区2018-2019学年七年级下学期数学期中考试试卷
试卷更新日期:2020-03-05 类型:期中考试
一、单选题
-
1. 目前,世界上能制造出的最小晶体管的长度只有0.000 000 04m,将0.000 000 04用科学记数法表示为( )A、4×108 B、4×10﹣8 C、0.4×108 D、﹣4×1082. 下面是一名学生所做的4道练习题:① ;② ;③ ;④ 。他做对的个数是( )A、1 B、2 C、3 D、43. 下列各式中,计算结果正确是( )A、 B、 C、 D、4. 小明在利用完全平方公式计算一个二项整式的平方时,不小心用墨水把最后一项染黑了,得到正确结果变为 ( ),你觉得这一项应是( )A、 B、 C、 D、5. 如图,通过计算大正方形的面积,可以验证的公式是( )
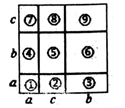 A、 B、 C、 D、6.
A、 B、 C、 D、6.如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )
 A、30° B、25° C、20° D、15°7. 如图,已知∠1=∠B,∠2=∠C,则下列结论不成立的是( )
A、30° B、25° C、20° D、15°7. 如图,已知∠1=∠B,∠2=∠C,则下列结论不成立的是( )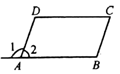 A、AB//CD B、AD//BC C、∠2+∠B=180° D、∠B=∠C8. 下列正确说法的个数是( )
A、AB//CD B、AD//BC C、∠2+∠B=180° D、∠B=∠C8. 下列正确说法的个数是( )①同位角相等;②等角的补角相等;③两直线平行,同旁内角相等;④在同一平面内,过一点有且只有一条直线与已知直线垂直.
A、1 B、2 C、3 D、49. 弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂重物的质量x(kg)有下面的关系,那么弹簧总长y(cm)与所挂重物x(kg)之间的关系式为( )x(kg)
0
1
2
3
4
5
6
y(cm)
12
12.5
13
13.5
14
14.5
15
A、y=0.5x+12 B、y=x+10.5 C、y=0.5x+10 D、y=x+1210. 如图,在△ABC中,AC=BC,有一动点P从点A出发,沿A→C→B→A匀速运动,则CP的长度s与时间t之间的函数关系用图象描述大致是( )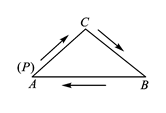 A、
A、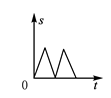 B、
B、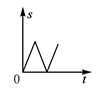 C、
C、 D、
D、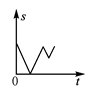
二、填空题
-
11. 若长方形的面积是3a2+2ab+3a,长为3a,则它的宽为 .12. 已知 ,则 n= .13. 若∠1与∠2互补,∠3与30°互余,∠2+∠3=200°,则∠1=度.14. 已知m﹣n=2,mn=﹣1,则(1+2m)(1﹣2n)的值为 .15. 若多项式5x2+2x﹣2与多项式ax+1的乘积中,不含x2项,则常数a= .16. 2(1+ )(1+ )(1+ )(1+ )+ = .17. 把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D,C分别在M,N的位置上,若∠EFG=56°,则∠1= , ∠2= .
 18. 已知(a-4)(a-2)=3,则(a-4)2+(a-2)2的值为 .19. 若规定符号 的意义是: = ,则当m2﹣2m﹣3=0时, 的值为 .
18. 已知(a-4)(a-2)=3,则(a-4)2+(a-2)2的值为 .19. 若规定符号 的意义是: = ,则当m2﹣2m﹣3=0时, 的值为 .三、解答题
-
20. 计算题(1)、计算:(2)、计算:(3)、用乘法公式计算:21. 先化简,再求值: ,其中 ,n=2.22. 已知 , ,求下列式子的值:(1)、 ;(2)、6ab.23.
如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.
 24. 如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
24. 如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.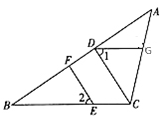 (1)、CD与EF平行吗?为什么?(2)、如果∠1=∠2,试判断DG与BC的位置关系,并说明理由.25. 周末,小明坐公交车到滨海公园游玩,他从家出发0.8小时后达到中心书城,逗留一段时间后继续坐公交车到滨海公园,小明离家一段时间后,爸爸驾车沿相同的路线前往海滨公园.如图是他们离家路程s(km)与小明离家时间t(h)的关系图,请根据图回答下列问题:
(1)、CD与EF平行吗?为什么?(2)、如果∠1=∠2,试判断DG与BC的位置关系,并说明理由.25. 周末,小明坐公交车到滨海公园游玩,他从家出发0.8小时后达到中心书城,逗留一段时间后继续坐公交车到滨海公园,小明离家一段时间后,爸爸驾车沿相同的路线前往海滨公园.如图是他们离家路程s(km)与小明离家时间t(h)的关系图,请根据图回答下列问题: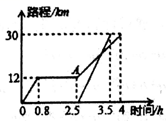 (1)、图中自变量是 , 因变量是;(2)、小明家到滨海公园的路程为km,小明在中心书城逗留的时间为h;(3)、小明出发小时后爸爸驾车出发;(4)、图中A点表示;(5)、小明从中心书城到滨海公园的平均速度为km/h,小明爸爸驾车的平均速度为km/h;(补充;爸爸驾车经过追上小明);(6)、小明从家到中心书城时,他离家路程s与坐车时间t之间的关系式为.26. “化归与转化的思想”是指在研究解决数学问题时采用某种手段将问题通过变换使之转化,进而使问题得到解决。(1)、我们知道 可以得到 。如果 ,求 、 的值.(2)、已知 试问多项式a2+b2+c2﹣ab﹣ac﹣bc的值是否与变量 的取值有关?若有关请说明理由;若无关请求出多项式的值.(3)、你认为图2中的阴影部分的正方形的边长等于.(4)、请用两种不同的方法求图2中阴影部分的面积.(5)、仔细观察图2,写出 三个代数式之间的等量关系.(6)、若 ,求 的值.27. 如图1,是一个长为 ,宽为 的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形。
(1)、图中自变量是 , 因变量是;(2)、小明家到滨海公园的路程为km,小明在中心书城逗留的时间为h;(3)、小明出发小时后爸爸驾车出发;(4)、图中A点表示;(5)、小明从中心书城到滨海公园的平均速度为km/h,小明爸爸驾车的平均速度为km/h;(补充;爸爸驾车经过追上小明);(6)、小明从家到中心书城时,他离家路程s与坐车时间t之间的关系式为.26. “化归与转化的思想”是指在研究解决数学问题时采用某种手段将问题通过变换使之转化,进而使问题得到解决。(1)、我们知道 可以得到 。如果 ,求 、 的值.(2)、已知 试问多项式a2+b2+c2﹣ab﹣ac﹣bc的值是否与变量 的取值有关?若有关请说明理由;若无关请求出多项式的值.(3)、你认为图2中的阴影部分的正方形的边长等于.(4)、请用两种不同的方法求图2中阴影部分的面积.(5)、仔细观察图2,写出 三个代数式之间的等量关系.(6)、若 ,求 的值.27. 如图1,是一个长为 ,宽为 的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形。 (1)、我们知道 可以得到 。如果 ,求 、 的值.(2)、已知 试问多项式a2+b2+c2﹣ab﹣ac﹣bc的值是否与变量 的取值有关?若有关请说明理由;若无关请求出多项式的值.(3)、你认为图2中的阴影部分的正方形的边长等于.(4)、请用两种不同的方法求图2中阴影部分的面积.(5)、仔细观察图2,写出 三个代数式之间的等量关系.(6)、若 ,求 的值.28. 如图,直线l1∥l2 , 直线l与l1、l2分别交于A、B两点,点M、N分别在l1、l2上,点M、N、P均在l的同侧(点P不在l1、l2上),若∠PAM=α,∠PBN=β.
(1)、我们知道 可以得到 。如果 ,求 、 的值.(2)、已知 试问多项式a2+b2+c2﹣ab﹣ac﹣bc的值是否与变量 的取值有关?若有关请说明理由;若无关请求出多项式的值.(3)、你认为图2中的阴影部分的正方形的边长等于.(4)、请用两种不同的方法求图2中阴影部分的面积.(5)、仔细观察图2,写出 三个代数式之间的等量关系.(6)、若 ,求 的值.28. 如图,直线l1∥l2 , 直线l与l1、l2分别交于A、B两点,点M、N分别在l1、l2上,点M、N、P均在l的同侧(点P不在l1、l2上),若∠PAM=α,∠PBN=β.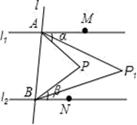 (1)、当点P在l1与l2之间时.
(1)、当点P在l1与l2之间时.①求∠APB的大小(用含α、β的代数式表示);
②若∠PAM的平分线与∠PBN的平分线交于点P1 , ∠P1AM的平分线与∠P1BN的平分线交于点P2 , …,∠Pn﹣1AM的平分线与∠Pn﹣1BN的平分线交于点Pn , 则∠AP1B= , ∠APnB= . (用含α、β的代数式表示,其中n为正整数)
(2)、当点P不在l1与l2之间时.若∠PAM的平分线与∠PBN的平分线交于点P1 , ∠P1AM的平分线与∠P1BN的平分线交于点P2 , …,∠Pn﹣1AM的平分线与∠Pn﹣1BN的平分线交于点Pn , 请直接写出∠APnB的大小.(用含α、β的代数式表示,其中n为正整数)