四川省成都市金塘县2018-2019学年七年级下学期数学期中考试试卷

试卷更新日期：2020-03-05 类型：期中考试

进入出卷网下载

一、单选题

1. 下列计算正确是（）

A、(x³)²=x⁹ B、(π-3.14)⁰=1 C、(5x)²= 10x² D、x⁵+x²=x³

查看试题解析
2. 下列图形中，∠1和∠2不是同位角的是（）

A、 B、 C、 D、

查看试题解析
3. 随着科技的进步，微电子技术飞跃发展，电子科学院的学生在实验室把半导体材料的尺寸大幅度缩小，某电子元件的面积大约为0.00 000 012平方笔米，0.00 000 012用科学记数法可表示为（）

A、 $1.2 \times 10^{- 6}$ B、 $1.2 \times 10^{- 8}$ C、 $1.2 \times 10^{- 7}$ D、 $0.12 \times 10^{- 6}$

查看试题解析
4. 下列各式不能用平方差公式计算的是（）

A、 $(- x - y) (x + y)$ B、 $(- x - y) (- x + y)$ C、 $(a b + c) (a b - c)$ D、 $(0.3 x - y) (- y - 0.3 x)$

查看试题解析
5. 下列说法错误的是（）

A、同角的余角相等 B、内错角相等 C、垂线段最短 D、平行于同一条直线的两条直线平行

查看试题解析
6. 已知： $x^{2} - 2 （ k + 1 ） x + 4$ 是一个完全平方式，则 $k$ 的值为（）

A、2 B、 $\pm 2$ C、1 D、1或-3

查看试题解析
7. 实践课上，张老师给同学们出了这样一道题：已知，如图点 $C$ 在 $∠ A O D$ 的边上，用尺规作出 $C N / / O A$ .小颖进行如图所示的操作，从作图的痕迹可以发现， $\overset{⌢}{F G}$ 是（）

A、以点 $C$ 为圆心， $O M$ 为半径的弧 B、以点 $C$ 为圆心， $D M$ 为半径的弧 C、以点 $E$ 为圆心， $O M$ 为半径的弧 D、以点 $E$ 为圆心， $D M$ 为半径的弧

查看试题解析
8. 如图， $A B ⊥ C D$ 于点 $O$ ，过点 $O$ 作直线 $E F$ ，使 $∠ C O E ： ∠ B O E = 3 ： 1$ .则 $∠ F O D$ 的度数为（）

A、22.5° B、77.5° C、67.5° D、60°

查看试题解析
9. 如图，直线 $A B / / C D$ ，将含有45°角的三角板 $E F P$ 的直角顶点 $F$ 放在直线 $C D$ 上.顶点 $E$ 放在直线 $A B$ 上，若 $∠ 1 = 28 °$ ，则∠2的度数为（）

A、45° B、17° C、25° D、30°

查看试题解析
10. 如图，在长方形ABCD中，点E为AB上一点，且CD=5，AD=2，AE=3，动点P从点E出发，沿路径E-B-C-D运动，则△DPE 的面积y与点P运动的路径长x之间的关系用图象表示大致为（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. $（ \frac{1}{2} ）^{- 2} =$ .

查看试题解析
12. 若 $∠ A = 37 ° 49'$ ，则 $∠ A$ 的补角为.

查看试题解析
13. 若a^m=2，aⁿ=3，则a^m+2n=.

查看试题解析
14. 为了积极响应习近平主席的号召，关注民生，为老百姓干实事，某工程队在某村修建一条长 $48 k m$ 的乡村公路，预计工期为120天，若每天修建公路的长度保持不变，则还未完成的公路的长度 $y （ k m ）$ 与施工时间 $x$ （天）之间的关系式为 $y =$ .

查看试题解析
15. $∠ A$ 与 $∠ B$ 的两边分别平行，且 $∠ A$ 比 $∠ B$ 的2倍少45°，则 $∠ A =$ .

查看试题解析

三、解答题

16. 计算:

(1)、 $（ - 2 a^{2} ）^{2} \cdot （ - 2 b^{2} ） \div 4 a^{3} b^{2}$

(2)、 $2019^{2} - 2017 \times 2021$ （用乘法公式进行计算）

查看试题解析
17. 如图，点 $E ， F$ 分别在直线 $A B ， C D$ 上，若 $∠ B N F + ∠ B M E = 180 ° ， ∠ A = ∠ D$ ，则 $∠ B = ∠ C$ .请说明理由.

解： $∵ ∠ B N F + ∠ B M E = 180 °$ ，

$∠ B M E = ∠ C M D$ ，

$∴ ∠ B N F + ∠ C M D = 180 ° ，$

$∴ A F / / E D$ ，

$∴ ∠ A F C = ∠ D$ .

又 $∵ A = ∠ D$ ，

$∴ ∠ A F C = ∠ A$ ，

$∴ A B / / C D$ ，

$∴ ∠ B = ∠ C$ .

查看试题解析
18. 先化简，再求值：
$3 (a - 2) (a + 2) - 3 (2 a + 1) - {(a - 3)}^{2}$ ，其中 $a$ 的值满足等式 $(x + 2) (2 x - 1) = 2 x^{2} + 3 x + a$ .

查看试题解析
19. 如图，在平行四边形ABCD中.当底边AB上的高x( cm)由小到大变化时，平行四边形ABCD的面积y( cm²)也随之发生变化，我们得到如下数据：

(1)、在这个变化过程中，自变量.因变量分别是什么?

(2)、y与x之间的关系式可以表示为.

(3)、由表格中的数据可以发现，当x每增加1 cm时，y如何变化?

(4)、若平行四边形ABCD的面积为21.6 cm² .此时底边AB上的高为多少?

查看试题解析
20. 为了改善小区环境，搞好绿化管理工作，更好地服务于居民，某小区物业绿化工作人员李师傅，规划在 $A B = （ a + 3 b ）$ 米， $A D = （ 3 a + 2 b ）$ 米的长方形的场地上，修建两横一纵三条宽为 $a$ 米的小路，其余部分铺上地毯草.

(1)、小路的面积总和为多少平方米？

(2)、所铺地毯草的面积和是多少平方米？

(3)、如果 $a = 1 ， b = 5$ ，并且每平方米地毯草的价格是20元，那么请你帮李师傅计算一下，买地毯草需要多少元？

查看试题解析
21. 星期五小颖放学步行从学校回家，当她走了一段路后，想起要去买彩笔做画报，于是原路返回到刚经过的文具用品店，买到彩笔后继续往家走.如图是她离家的距离与所用时间的关系示意图，请根据图中提供的信息回答下列问题：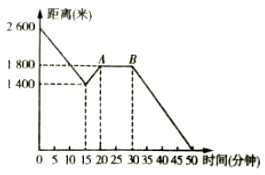

(1)、小颖家与学校的距离是米；

(2)、 $A B$ 表示的实际意义是；

(3)、小颖本次从学校回家的整个过程中，走的路程是多少米？

(4)、买到彩笔后，小颖从文具用品店回到家步行的速度是多少米/分？

查看试题解析
22. 在学习“乘法公式“时，育红中学七（1）班数学兴趣小组在活动课上进行了这样的操作：作两条互相垂直的线段 $A B$ 和 $C D$ ，把大正方形分成四部分（如图所示）.
观察发现

(1)、请用两种不同的方法表示图形的面积，得到一个等量关系：.

(2)、请你作一个图形验证： $(x + y) (2 x + y) = 2 x^{2} + 3 x y + y^{2}$ .

(3)、若 $A B + C D = 14$ ，如图中阴影部分的面积和为13，求 $x y$ 的值.

查看试题解析
23. 已知，如图，把直角三角形 $M O N$ 的直角顶点 $O$ 放在直线 $A B$ 上，射线 $O C$ 平分 $∠ A O N$ .

(1)、如图，若 $∠ M O C = 28 °$ ，求 $∠ B O N$ 的度数.

(2)、若 $∠ M O C = m °$ ，则 $∠ B O N$ 的度数为.

(3)、由（1）和（2），我们发现 $∠ M O C$ 和 $∠ B O N$ 之间有什么样的数量关系？

(4)、若将三角形 $M O N$ 绕点 $O$ 旋转到如图所示的位置，试问 $∠ M O C$ 和 $∠ B O N$ 之间的数量关系是否发生变化？请说明理由.

查看试题解析