山西省太原市2017-2018学年七年级下学期数学期中考试试卷

试卷更新日期：2020-03-05 类型：期中考试

进入出卷网下载

一、单选题

1. 计算2^﹣²的结果是（）

A、4 B、﹣4 C、 $\frac{1}{4}$ D、﹣ $\frac{1}{4}$

查看试题解析
2. 下列说法正确是（）

A、同旁内角互补 B、在同一平面内，若a⊥b，b⊥c，则a⊥c C、对顶角相等 D、一个角的补角一定是钝角

查看试题解析
3. 下列运算正确是（）

A、a^﹣³÷a^﹣⁵＝a² B、(3a²)³＝9a⁵ C、(x﹣1)(1﹣x)＝x²﹣1 D、(a+b)²＝a²+b²

查看试题解析
4. 如图，直线a、b被直线c所截，下列条件：(1)∠1＝∠3；(2)∠3＝∠4；(3)∠1＝∠4；(4)∠2+∠4＝180°，其中能判定a∥b的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 纳米是一种长度单位，1米＝10⁹纳米，已知某种植物花粉的直径约为35000纳米，那么用科学记数法表示这种花粉的直径为（）

A、3.5×10^﹣⁶米 B、3.5×10^﹣⁵米 C、35×10¹³米 D、3.5×10¹³米

查看试题解析
6. 出生1﹣6个月的婴儿生长发育得非常快，他们的体重y(克)与月龄x(月)间的关系可以用y＝a+700x来表示，其中a是婴儿出生时的体重，一个婴儿出生时的体重是3000克，这个婴儿第4个月的体重为（）

A、6000克 B、5800克 C、5000克 D、5100克

查看试题解析
7. 如图，点O在直线AB上，OC⊥AB，∠DOE＝90°，则∠AOD的余角是（）

A、∠COD B、∠COE C、∠COE和∠COD D、∠COD和∠BOE

查看试题解析
8. 按图(1)﹣(3)的方式摆放餐桌和椅子，照这样的方式维续摆放，如果摆放的餐桌为x张，摆放的椅子为y把，则y与x之间的关系式为（）

A、y＝6x B、y＝4x﹣2 C、y＝5x﹣1 D、y＝4x+2

查看试题解析
9. 小明看到了一首诗：“儿子学成今日返，老父早早到车站，儿子到后细端详，父子高兴把家还”，读完后，他想用图象描述这首诗的内容，如果用纵轴表示父亲与儿子行进中离家的距离，横轴表示父亲离家的时间，那么下列图象中大致符合这首诗含义的是（）

A、 B、 C、 D、

查看试题解析
10. 已知 $a = 81^{31} ， b = 27^{41} ， c = 9^{61} ，$ 则 $a 、 b 、 c$ 的大小关系是（）

A、 $a > b > c$ B、 $a > c > b$ C、 $a < b < c$ D、 $b > c > a$

查看试题解析

二、填空题

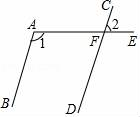
11. 计算(﹣x³)²的结果是．

查看试题解析
12. 如图，AB∥CD，射线AE交CD于点F，若∠1＝116°，则∠2的度数等于．

查看试题解析
13. 地表以下岩层的温度y(℃)随着所处深度x(km)的变化而变化，在某个地点y与x之间有如下关系：

x/km

1

2

3

4

Y/℃

55

90

125

160

根据表格，估计地表以下岩层的温度为230℃时，岩层所处的深度为km．

查看试题解析
14. 如图中阴影部分的面积等于．

查看试题解析
15. 南宋数学家杨辉在研究(a+b)ⁿ展开式各项的系数时，采用了特殊到一般的方法，他将(a+b)⁰ ， (a+b)¹ ， (a+b)² ， (a+b)³ ， …，展开后各项的系数画成如图所示的三角阵，在数学上称之为杨辉三角．已知(a+b)⁰＝1，(a+b)¹＝a+b，(a+b)²＝a²+2ab+b² ， (a+b)³＝a³+3a²b+3ab²+b³ ．按杨辉三角写出(a+b)⁵的展开式是．

查看试题解析

三、解答题

16. 计算：

(1)、(﹣3x²y)²•(6xy³)÷(9x³y⁴)

(2)、(x﹣y)(x+y)﹣4y(x﹣y)

查看试题解析
17. 先化简，再求值：
（x﹣2y）²﹣x（x+3y）﹣4y² ，其中x=﹣4，y= $\frac{1}{2}$ ．

查看试题解析
18. 如图，填空并填写理由：

(1)、因为∠1=∠2，所以AD∥BC ．

(2)、因为∠A+∠ABC=180°，所以AD∥BC ．

(3)、因为∥ ，所以∠C+∠ABC=180°(两直线平行，同旁内角互补)

(4)、因为∥ ，所以∠3=∠C(两直线平行，同位角相等)．

查看试题解析
19. 如图，已知点M在射线ON上，∠α，∠β．从A、B两题中任选一题完成尺规作图：
A．求作∠POM，使得∠POM＝∠α+∠β

B．求作点P，使得∠POM＝∠α，∠PMO＝∠β

要求：不写作法，保留作图痕迹，标明字母．

查看试题解析
20. 根据几何图形的面积关系可以形象直观地表示多项式的乘法，例如(a+b)(p+q)=ap+aq+bp+bq可以用图(1)表示：

(1)、根据图(2)，写出一个多项式乘以多项式的等式.

(2)、从A、B两题中任选一题作答.
A．请画一个几何图形，表示(x+p)(x+q)=x²+(p+q)x+pq，并仿照上图标明相应的字母.

B．请画一个几何图形，表示(x-p)(x-q)=x²-(p+q)x+pq，并仿照上图标明相应的字母.

查看试题解析
21. 如图，AD⊥BC于点D，EF⊥BC于点F，∠BDG＝∠C．试说明∠1＝∠2．

查看试题解析
22. 小明骑自行车上学，某天他从家出发骑行了一段路程，想起要买一本书，于是折回到他刚经过的某书店，买到书后继续去学校．以下是他在本次上学离家的距离与所用的时间的关系示意图，根据图中提供的信息解答下列问题：

(1)、小明家与学校的距离是米．

(2)、小明在书店停留了多少分钟？

(3)、从A，B两题中任选一题作答：
A．小明骑行过程中哪个时间段的速度最快，最快的速度是多少？

B．小明在这次上学过程中的平均速度是多少？

查看试题解析
23. 问题情境
在综合与实践课上，老师让同学们以“两条平行线AB，CD和一块含60°角的直角三角尺EFG(∠EFG＝90°，∠EGF＝60°)”为主题开展数学活动．

操作发现

(1)、如图(1)，小明把三角尺的60°角的顶点G放在CD上，若∠2＝2∠1，求∠1的度数；

(2)、如图(2)，小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上，请你探索并说明∠AEF与∠FGC之间的数量关系；
结论应用

(3)、如图(3)，小亮把三角尺的直角顶点F放在CD上，30°角的顶点E落在AB上．若∠AEG＝α，则∠CFG等于(用含α的式子表示)．

查看试题解析

x/km	1	2	3	4
Y/℃	55	90	125	160