四川省资阳市雁江区2018-2019学年八年级下学期数学期中考试试卷
试卷更新日期:2020-03-05 类型:期中考试
一、单选题
-
1. 下列各式: , , +y, , ,其中分式共有( )A、1个 B、2个 C、3个 D、4个2. 若分式 的值为零,则x的取值为( )A、x≠3 B、x≠-3 C、x=3 D、x=-33. 若▱ABCD中,∠A+∠C=160°,则∠D的度数是( )A、120° B、100° C、60° D、70°4. 生物学家发现了某种花粉的直径约为0.0000036毫米,数据0.0000036用科学记数法表示正确是( )A、3.6×10﹣5 B、0.36×10﹣5 C、3.6×10﹣6 D、0.36×10﹣65. 已知一次函数y=(m+2)x+(1-m),若y随x的增大而减小,且此函数图象与y轴的交点在x轴的上方,则m的取值范围是( )A、m>-2 B、m<1 C、m<-2 D、-2<m<16. 若关于x的方程 = 有增根,则m的值为( )A、0 B、1 C、-1 D、27. 若式子 +(k-1)0有意义,则一次函数y=(1-k)x+k-1的图象可能是( )A、
 B、
B、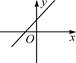 C、
C、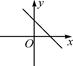 D、
D、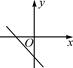 8. 如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数y= 的图象交于A,B两点,则四边形MAOB的面积为( )
8. 如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数y= 的图象交于A,B两点,则四边形MAOB的面积为( )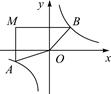 A、6 B、8 C、10 D、129. 若关于x的方程 + =3的解为正数,则m的取值范围是( )A、m< B、m< 且m≠ C、m>﹣ D、m>﹣ 且m≠﹣10. 如图①,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图②所示,则当x=4时,点R应运动到( )
A、6 B、8 C、10 D、129. 若关于x的方程 + =3的解为正数,则m的取值范围是( )A、m< B、m< 且m≠ C、m>﹣ D、m>﹣ 且m≠﹣10. 如图①,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图②所示,则当x=4时,点R应运动到( )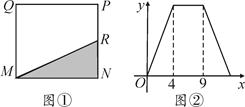 A、P处 B、Q处 C、M处 D、N处
A、P处 B、Q处 C、M处 D、N处二、填空题
-
11. 计算: = .12. 函数y= 的自变量x的取值范围是 .13. 直线y=3x+2沿y轴向下平移5个单位,则平移后的直线与y轴的交点坐标是.14. 若a2+5ab-b2=0,则 - 的值为 .15. 已知点 在直线 上,也在双曲线 上,则 的值为.16. 若点A(-2,y1),B(-1,y2),C(1,y3)都在反比例函数y= (k为常数)的图象上,则y1 , y2 , y3的大小关系为 . (用“<”连接)
三、解答题
-
17.(1)、计算(π-3.14)0+( )-1-|-4|+2-2(2)、化简: - ÷ .18. 解分式方程(1)、 + =2.(2)、 +1= .19. 已知一次函数y=(6+3m)x+n-4.(1)、当m,n为何值时,函数的图象过原点?(2)、当m,n满足什么条件时,函数的图象经过第一、二、三象限?20. 先化简( -a+1)÷ ,并从0,-1,2中选一个合适的数作为a的值代入求值.21. 在▱ABCD中,点E、F分别在AB、CD上,且AE=CF.
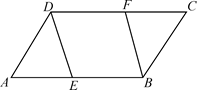 (1)、求证:△ADE≌△CBF;(2)、求证:四边形DEBF为平行四边形.22. 小明和小刚相约周末到雪莲大剧院看演出,他们的家分别距离剧院1200m和2000m,两人分别从家中同时出发,已知小明和小刚的速度比是3:4,结果小明比小刚提前4min到达剧院.求两人的速度.
(1)、求证:△ADE≌△CBF;(2)、求证:四边形DEBF为平行四边形.22. 小明和小刚相约周末到雪莲大剧院看演出,他们的家分别距离剧院1200m和2000m,两人分别从家中同时出发,已知小明和小刚的速度比是3:4,结果小明比小刚提前4min到达剧院.求两人的速度.
23. 已知反比例函数的图象经过三个点A(﹣4,﹣3),B(2m,y1),C(6m,y2),其中m>0.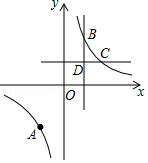 (1)、当y1﹣y2=4时,求m的值;(2)、如图,过点B、C分别作x轴、y轴的垂线,两垂线相交于点D,点P在x轴上,若三角形PBD的面积是8,请写出点P坐标(不需要写解答过程).24. 某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒的售价比乙种羽毛球多15元,王老师从该网店购买了2筒甲种羽毛球和3筒乙种羽毛球,共花费255元.
(1)、当y1﹣y2=4时,求m的值;(2)、如图,过点B、C分别作x轴、y轴的垂线,两垂线相交于点D,点P在x轴上,若三角形PBD的面积是8,请写出点P坐标(不需要写解答过程).24. 某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒的售价比乙种羽毛球多15元,王老师从该网店购买了2筒甲种羽毛球和3筒乙种羽毛球,共花费255元.
(1)、该网店甲、乙两种羽毛球每筒的售价各是多少元?(2)、根据消费者需求,该网店决定用不超过8780元购进甲、乙两种羽毛球共200筒,且甲种羽毛球的数量大于乙种羽毛球数量的 ,已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.①若设购进甲种羽毛球m筒,则该网店有哪几种进货方案?
②若所购进羽毛球均可全部售出,请求出网店所获利润W(元)与甲种羽毛球进货量m(筒)之间的函数关系式,并说明当m为何值时所获利润最大?最大利润是多少?