四川省邛崃市2018-2019学年八年级下学期数学期中考试试卷

试卷更新日期：2020-03-05 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各式变形中，是因式分解的是（　　）

A、a²﹣2ab+b²﹣1=（a﹣b）²﹣1 B、2x²+2x=2x²（1+ $\frac{1}{x}$ ） C、（x+2）（x﹣2）=x²﹣4 D、x⁴﹣1=（x²+1）（x+1）（x﹣1）

查看试题解析
2. 下图中是中心对称图形而不是轴对称图形的共有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 下列多项式中，能用平方差公式分解因式的是（）

A、 $a^{2} + {(- b)}^{2}$ B、 ${5m}^{2} -20mn$ C、 $- x^{2} - y^{2}$ D、 $- x^{2} + 25$

查看试题解析
4. 观察图形，可以得出不等式组 ${\begin{matrix} a x + b > 0 \\ c x + d < 0 \end{matrix}$ 的解集是（　）

A、x＜﹣1 B、x＜4 C、﹣1＜x＜0 D、﹣1＜x＜4

查看试题解析
5. 无论a取何值时，下列分式一定有意义的是（）

A、 $\frac{a^{2} + 1}{a^{2}}$ B、 $\frac{a + 1}{a^{2}}$ C、 $\frac{a^{2} - 1}{a + 1}$ D、 $\frac{a - 1}{a^{2} + 1}$

查看试题解析
6. 下列各分式中，最简分式是（）

A、 $\frac{12 (x - y)}{15 (x + y)}$ B、 $\frac{y^{2} - x^{2}}{x + y}$ C、 $\frac{x^{2} + y^{2}}{x^{2} y + x y^{2}}$ D、 $\frac{x^{2} - y^{2}}{{(x + y)}^{2}}$

查看试题解析
7. 在如图所示的正方形网格中，网格线的交点称为格点，已知A、B是两格点，如果 C也是图中的格点，且使得△ABC为等腰直角三角形，则这样的点C有（）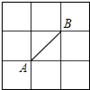

A、6个 B、7个 C、8个 D、9个

查看试题解析
8. 已知0≤a–b≤1且1≤a+b≤4，则a的取值范围是（）

A、1≤a≤2 B、2≤a≤3 C、 $\frac{1}{2}$ ≤a≤ $\frac{5}{2}$ D、 $\frac{3}{2}$ ≤a≤ $\frac{5}{2}$

查看试题解析
9. 下列各式从左到右的变形正确是（）

A、 $\frac{a^{2} - 0.2 a}{a^{2} - 0.3 a^{3}} = \frac{a^{2} - 2 a}{a^{2} - 3 a^{3}}$ B、 $- \frac{x + y}{x - y} = \frac{x - 1}{x - y}$ C、 $\frac{1 - \frac{1}{2} a}{a + \frac{1}{3}} = \frac{6 - 3 a}{6 a + 2}$ D、 $\frac{b^{2} - a^{2}}{a + b} = a - b$

查看试题解析
10. “五一”期间，某中学数学兴趣小组的同学们租一辆小型巴士前去某地进行社会实践活动，租车租价为180元.出发时又增加了两位同学，结果每位同学比原来少分摊了3元车费.若小组原有x人，则所列方程为（）

A、 $\frac{180}{x} - \frac{180}{x - 2} = 3$ B、 $\frac{180}{x} - \frac{180}{x + 2} = 3$ C、 $\frac{180}{x + 2} - \frac{180}{x} = 3$ D、 $\frac{180}{x - 2} - \frac{180}{x} = 3$

查看试题解析

二、填空题

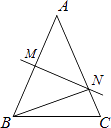
11. 因式分解：9a³b﹣ab＝.

查看试题解析
12. 已知当x=2时，分式 $\frac{x + a}{2 x - b}$ 的值为0；当x=1时，分式无意义．则a－b= ．

查看试题解析
13. 如图，在△ABC中，AB=AC=3cm，AB的垂直平分线交AC于点N，△BCN的周长是5cm，则BC的长等于 cm．

查看试题解析
14. 若y²+my+16是完全平方式，则m=

查看试题解析
15. 如图，在△ABC中，D为BC的中点，以D为圆心，BD长为半径画一弧交AC于E点，若∠A＝60°，∠B＝100°，BC＝2，则扇形BDE的面积为．

查看试题解析
16. 若m+n=1，mn=2，则 $\frac{1}{m} + \frac{1}{n}$ 的值为．

查看试题解析
17. 如图，已知函数y＝3x+b和y＝ax﹣3的图象交于点P（﹣2，﹣5），则根据图象可得不等式3x+b＞ax﹣3的解集是.

查看试题解析
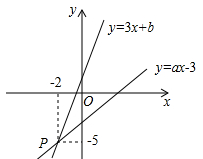18. 若分式方程式 $\frac{x - 1}{x - 2} = \frac{m}{x - 2} + 2$ 无解，则m的值为．

查看试题解析
19. 已知，在平面直角坐标系中，点M、N的坐标分别为（1，4）和（3，0），点Q是y轴上的一个动点，且M、N、Q三点不在同一直线上，当△MNQ的周长最小时，则点Q的坐标是．

查看试题解析
20. 已知△ABC中，∠ABC＝45°，AB＝7 $\sqrt{2}$ ，BC＝17，以AC为斜边在△ABC外作等腰Rt△ACD，连接BD，则BD的长为．

查看试题解析

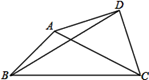
三、解答题

21. 计算与化简：

(1)、解不等式组 ${\begin{array}{l} 5 x - 2 \geq 3 (x + 1) \\ \frac{1}{2} x - 1 < 7 - 1.5 x \end{array}$ ，并把其解集在数轴上表示出来．

(2)、解方程： $\frac{x - 2}{x + 2} = \frac{x + 2}{x - 2} + \frac{16}{x^{2} - 4}$

(3)、化简求值： $\frac{x^{2} - 2 x}{x^{2} - 1} \div (x - 1 - \frac{2 x - 1}{x + 1})$ ，其中 $x = \frac{1}{2}$ ．

查看试题解析
22. 如图，在平面直角坐标系xOy中，△ABC的三个顶点坐标分别为A（1，1），B（4，0），C（4，4）．

(1)、按下列要求作图：
①将△ABC向左平移4个单位，得到△A₁B₁C₁；

②将△A₁B₁C₁绕点B₁逆时针旋转90°，得到△A₂B₂C₂ ．

(2)、求点C₁在旋转过程中所经过的路径长．

查看试题解析
23. 在2016年“双十一”期间，某快递公司计划租用甲、乙两种车辆快递货物，从货物量来计算：若租用两种车辆合运，10天可以完成任务；若单独租用乙种车辆，完成任务的天数是单独租用甲种车辆完成任务天数的2倍．

(1)、求甲、乙两种车辆单独完成任务分别需要多少天？

(2)、已知租用甲、乙两种车辆合运需租金65000元，甲种车辆每天的租金比乙种车辆每天的租金多1500元，试问：租甲和乙两种车辆、单独租甲种车辆、单独租乙种车辆这三种租车方案中，哪一种租金最少？请说明理由．

查看试题解析
24. 阅读下列材料：
在学习“可化为一元一次方程的分式方程及其解法”的过程中，老师提出一个问题：若关于x的分式方程 $\frac{a}{x - a}$ =1的解为正数，求a的取值范围．

经过独立思考与分析后，小杰和小哲开始交流解题思路如下：

小杰说：解这个关于x的分式方程，得x=a+4．由题意可得a+4＞0，所以a＞﹣4，问题解决．

小哲说：你考虑的不全面，还必须保证x≠4，即a+4≠4才行．

(1)、请回答：的说法是正确，并简述正确理由是；

(2)、参考对上述问题的讨论，解决下面的问题：
若关于x的方程 $\frac{m}{x - 3} - \frac{x}{3 - x} = 2$ 的解为非负数，求m的取值范围．

查看试题解析
25. 已知△ABC为等边三角形，点D为直线BC上的一动点(点D不与B、C重合)，以AD为边作等边△ADE(顶点A、D、E按逆时针方向排列)，连接CE．

(1)、如图1，当点D在边BC上时，求证：①BD＝CE，②AC＝CE+CD；

(2)、如图2，当点D在边BC的延长线上且其他条件不变时，结论AC＝CE+CD是否成立？若不成立，请写出AC、CE、CD之间存在的数量关系，并说明理由；

(3)、如图3，当点D在边BC的反向延长线上且其他条件不变时，补全图形，并直接写出AC、CE、CD之间存在的数量关系．

查看试题解析
26. 因为 $\frac{1}{1 \times 2} = 1 - \frac{1}{2}$ ， $\frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3}$ …， $\frac{1}{19 \times 20} = \frac{1}{19} - \frac{1}{20}$ ，
所以 $\frac{1}{1 \times 2}$ + $\frac{1}{2 \times 3}$ +…+ $\frac{1}{19 \times 20}$ ＝1﹣ $\frac{1}{2}$ + $\frac{1}{2}$ ﹣ $\frac{1}{3}$ +…+ $\frac{1}{19}$ ﹣ $\frac{1}{20}$ ＝1﹣ $\frac{1}{20}$ ＝ $\frac{19}{20}$ ．

解答下列问题：

(1)、在和式 $\frac{1}{1 \times 2}$ + $\frac{1}{2 \times 3}$ + $\frac{1}{3 \times 4}$ +…中，第九项是；第n项是．

(2)、解方程 $\frac{1}{(x + 1) (x + 2)} + \frac{1}{(x + 2) (x + 3)} + \dots + \frac{1}{(x + 2001) (x + 2002)} = 1 - \frac{2}{2 x + 4004}$ ．

查看试题解析
27. “绿水青山，就是金山银山”．某旅游景区为了保护环境，需购买 $A 、 B$ 两种型号的垃圾处理设备共10台，已知每台 $A$ 型设备日处理能力为12吨；每台 $B$ 型设备日处理能力为15吨，购回的设备日处理能力不低于140吨.

(1)、请你为该景区设计购买 $A 、 B$ 两种设备的方案；

(2)、已知每台 $A$ 型设备价格为3万元，每台 $B$ 型设备价格为4.4万元.厂家为了促销产品，规定货款不低于40万元时，则按9折优惠；问:采用(1)设计的哪种方案，使购买费用最少，为什么?

查看试题解析
28. 问题背景：我们学习等边三角形时得到直角三角形的一个性质：在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半．即：如图1，在Rt△ABC中，∠ACB=90°，∠ABC=30°，则：AC= $\frac{1}{2}$ AB．

探究结论：小明同学对以上结论作了进一步研究．

(1)、如图1，连接AB边上中线CE，由于CE= $\frac{1}{2}$ AB，易得结论：
①△ACE为等边三角形；

②BE与CE之间的数量关系为．

(2)、如图2，点D是边CB上任意一点，连接AD，作等边△ADE，且点E在∠ACB的内部，连接BE．试探究线段BE与DE之间的数量关系，写出你的猜想并加以证明．

(3)、当点D为边CB延长线上任意一点时，在（2）条件的基础上，线段BE与DE之间存在怎样的数量关系？请直接写出你的结论．

(4)、拓展应用：如图3，在平面直角坐标系xOy中，点A的坐标为（﹣ $\sqrt{3}$ ，1），点B是x轴正半轴上的一动点，以AB为边作等边△ABC，当C点在第一象限内，且B（2，0）时，求C点的坐标．

查看试题解析