四川省简阳市简城学区、镇金学区2018-2019学年八年级下学期数学期中考试试卷
试卷更新日期：2020-03-05 类型：期中考试
一、单选题
-
1. 下列图案中，既是中心对称图形又是轴对称图形的是( )A、
B、
C、
D、
2. 如图，不等式组 的解集在数轴上表示正确是（ ）A、
B、
C、
D、
3. 下列命题是真命题的是（ ）．
A、有两条边、一个角相等的两个三角形全等。 B、等腰三角形的对称轴是底边上的中线。 C、全等三角形对应边上的中线相等。 D、有一个角是60°的三角形是等边三角形。4. 如图，在△ABC中，AB=AD=DC，∠B=70°，则∠C的度数为（ ）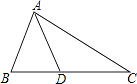
A、35° B、40° C、45° D、50°5. 在平面直角坐标系中，将点A(x，y)向右平移1个单位长度，再向下平移1个单位长度后与点B(3，－2)重合，则点A的坐标是( )A、(2，－3) B、(4，1) C、(4，－1) D、(2，－1)6. 小明和爸爸、妈妈三人玩跷跷板．三人的体重一共为150千克，爸爸坐在跷跷板的一端，体重只有妈妈一半的小明和妈妈一同坐在跷跷板的另一端．这时爸爸那端仍然着地，那么小明的体重应小于( )A、49千克 B、50千克 C、24千克 D、25千克7. 已知关于x的方程3x﹣a+1=2x﹣1的解为负数，则a的取值范围是（ ）A、a≥﹣2 B、a＞﹣2 C、a≤2 D、a＜28. 如图，△ABC中，∠B=55°，∠C=30°，分别以点A和点C为圆心，大于 AC的长为半径画弧，两弧相交于点M，N作直线MN，交BC于点D，连结AD，则∠BAD的度数为（ ）
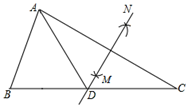A、65° B、60° C、55° D、45°9. 如图，∠A=50°，P是等腰△ABC内一点，且∠PBC=∠PCA，则∠BPC为（ ）
A、100° B、140° C、130° D、115°10. 如图，将边为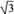
的正方形ABCD绕点A沿逆时针方向旋转30°后得到正方形AEFH，则图中阴影部分的面积为（ ） 
A、 － B、3－ C、2－ D、2－二、填空题
-
11. 命题“全等三角形的面积相等”的逆命题是命题．（填入“真”或“假”）12. 如图，△A′B′C′是由△ABC沿BC方向平移3个单位长度得到的，则点A与点A′的距离等于个单位长度．
13. 当x时，代数式 的值是非负数．14.如图是一次函数的y=kx+b图象，则关于x的不等式kx+b＞0的解集为
15.如图是3×4正方形网格，其中已有5各小方格涂上阴影，若再选取标有①，②，③，④中的一个小方格涂上阴影，使图中所有涂上阴影的小方格组成一个中心对称图形，则该小方格是 ． （填序号）
16. 不等式组 有3个整数解，则m的取值范围是 ．17. 某商场店庆活动中，商家准备对某种进价为600元、标价为1100元的商品进行打折销售，但要保证利润率不低于10%，则最多打折.18. 若关于x、y的二元一次方程组 的解满足x+y＞0，则m的取值范围是 ．19. 已知关于 的不等式组 只有3个整数解，则实数 的取值范围是 ．20. 如图，正△ABC的边长为2，以BC边上的高AB1为边作正△AB1C1 ， △ABC与△AB1C1公共部分的面积记为S1；再以正△AB1C1边B1C1上的高AB2为边作正△AB2C2 ， △AB1C1与△AB2C2公共部分的面积记为S2；…，以此类推，则Sn＝ ． （用含n的式子表示）
21. 如图，在Rt△ABC中，∠C=90°，∠B=60°，点D是BC边上的点，CD=1，将△ABC沿直线AD翻折，使点C落在AB边上的点E处，若点P是直线AD上的动点，则△PEB的周长的最小值是 ．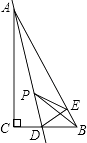
三、解答题
-
22.(1)、解不等式 并将它的解集在数轴上表示出来；(2)、解不等式2x－1＞ ，并将它的解集在数轴上表示出来；(3)、解不等式组 ，并写出它的整数解．(4)、解不等式组 并写出它的正整数解．23. 如图，在平面直角坐标系中，△ABC的三个顶点的坐标分别为A（﹣3，5），B（﹣4，3），（﹣1，1）．
(1)、作出△ABC向右平移5个单位的△A1B1C1；(2)、作出△ABC关于x轴对称的△A2B2C2 ， 并写出点C2的坐标．24. 从①∠B=∠C；②∠BAD=∠CDA；③AB=DC；④BE=CE四个等式中选出两个作为条件，证明△AED是等腰三角形（写出一种即可）．
已知： （只填序号）
求证：△AED是等腰三角形.
证明：
