四川省成都市高新区2018-2019学年八年级下学期数学期中考试试卷

试卷更新日期：2020-03-05 类型：期中考试

进入出卷网下载

一、单选题

1. 在下列英文大写正体字母中，是中心对称图形的选项是（）

A、V B、W C、X D、Y

查看试题解析
2. 下列不等式变形正确是（）

A、由a＞b，得a+1＜b+1 B、由 $a > b$ ，得 $- 3 a < - 3 b$ C、由a＞b，得 $2 a < 2 b$ D、由 $a > b$ ，得 $2 a - 3 < 2 b - 3$

查看试题解析
3. 下列各式，从左到右的变形是因式分解的是（）

A、 $a (x + y) = a x + a y$ B、 $2 x^{2} - x = x (2 x - 1)$ C、 $x^{2} + 4 x + 4 = x (x + 4) + 4$ D、 $x^{2} - 9 = (x + 9) (x - 9)$

查看试题解析
4. 下列命题正确是（）

A、在同一平面内，可以把半径相等的两个圆中的一个看成是由另一个平移得到的. B、两个全等的图形之间必有平移关系. C、三角形经过旋转，对应线段平行且相等. D、将一个封闭图形旋转，旋转中心只能在图形内部.

查看试题解析
5. 若分式 $\frac{x - 1}{x - 2}$ 有意义，则实数x的取值范围是（）

A、一切实数 B、 $x \neq 1$ C、 $x \neq 2$ D、 $x \neq 1$ 且 $x \neq 2$

查看试题解析
6. 用反证法证明命题“一个三角形中不能有两个角是直角”，应先假设这个三角形中（）

A、有两个角是直角 B、有另个角是钝角 C、有两个角是锐角 D、三个角都是直角

查看试题解析
7. 如图，一次函数 $y = k x + b$ 的图象经过点A( $1$ ，0)，B( $2$ ，1)，当因变量y>0时，自变量x的取值范围是（）

A、 $x > 0$ B、 $x < 0$ C、 $x > 1$ D、 $x < 1$

查看试题解析
8. 下列分式从左到右的变形正确是（）

A、 $\frac{x}{y} = \frac{x + 2}{y + 2}$ B、 $\frac{x}{y} = \frac{x^{2}}{y^{2}}$ C、 $\frac{x - 2}{x} = - \frac{x + 2}{x}$ D、 $\frac{5}{5 (x + 2)} = \frac{1}{x + 2}$

查看试题解析
9. 如图，在△ABC中，AB边垂直平分线MD交BC于点D，AC边垂直平分线EN交BC于点E，连接AD，AE，若∠BAC＝110°，则∠DAE的度数为（）

A、70° B、55° C、45° D、40°

查看试题解析
10. 已知关于x的不等式组 ${\begin{matrix} x + 3 > m \\ 2 x < m \end{matrix}$ 有解，则m的取值范围为（）

A、 $m > 6$ B、 $m \geq 6$ C、 $m < 6$ D、 $m \leq 6$

查看试题解析

二、填空题

11. 在等腰△ABC中，AB=AC，若∠A=80°，则∠C的度数为.

查看试题解析
12. 若关于x的不等式组 ${\begin{cases} x > m \\ x - n < 2 \end{cases}$ 的解集为 $1 < x < 3$ ，则m+n=.

查看试题解析
13. 若 $x^{2} + k x + 9$ 是一个完全平方式，则 $k$ =.

查看试题解析
14. 如图，在△ABC中，∠B=90°，BC =5cm，AB=12cm，则图中4个小直角三角形周长的和为cm.

查看试题解析
15. 若多项式 $x^{2} - 3 x + k$ 的一个因式是 $x - 2$ ，则k的值为.

查看试题解析
16. 已知关于x的不等式组 ${\begin{cases} x \leq a \\ 2 x - 3 > 1 \end{cases}$ 只有三个整数解，则实数a的取值范围是.

查看试题解析
17. 如图，△ABC的周长为12，OB、OC分别平分∠ABC和∠ACB，过点O作OD⊥BC于点D，OD=3，则△ABC的面积为.

查看试题解析
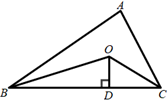18. 阅读材料：
分离整数法就是将分式拆分成一个整式与一个分式(分子为整数)的和的形式．如：

① $\frac{x + 1}{x - 1} = \frac{x - 1 + 2}{x - 1} = \frac{x - 1}{x - 1} + \frac{2}{x - 1} = 1 + \frac{2}{x - 1}$ ；

② $\frac{x^{2} + 1}{x - 3}$ = $\frac{x^{2} - 9 + 10}{x - 3}$ = $\frac{x^{2} - 9}{x - 3}$ + $\frac{10}{x - 3}$ =x+3+ $\frac{10}{x - 3}$ .

解答问题．已知x为整数，且分式 $\frac{3 x - 4}{x - 2}$ 为整数，则x的值为.

查看试题解析
19. 如图，Rt△ABC中，AB=AC=8，BO= $\frac{1}{4}$ AB，点M为BC边上一动点，将线段OM绕点O按逆时针方向旋转90°至ON，连接AN、CN，则△CAN周长的最小值为.

查看试题解析

三、解答题

20.

(1)、解不等式： $\frac{x + 5}{2} - 1 < \frac{2 x + 1}{3}$ .

(2)、因式分解： $2 a x^{2} - 8 a$ .

(3)、计算： $6 x y^{2} \div \frac{2 y^{2}}{x}$ .

查看试题解析
21. 如图：在平面直角坐标系中，网格中每一个小正方形的边长为1个单位长度，△ABC的顶点均在格点上，三个顶点的坐标分别是A(-3，4)，B(-2，1)，C(-4，2).

(1)、将△ABC先向右平移7个单位长度，再向上平移2个单位长度，画出第二次平移后的△ $A_{1} B_{1} C_{1}$ ；

(2)、以点O(0，0)为对称中心，画出与△ABC成中心对称的△ $A_{2} B_{2} C_{2}$ ；

(3)、将点B绕坐标原点逆时针方向旋转90°至点 $B_{3}$ ，求点 $B_{3}$ 的坐标

查看试题解析
22. 先化简，再求值： $\frac{x^{2} - 2 x}{x^{2} - 3 x} \div \frac{x^{2} - 4}{x^{2} - 6 x + 9}$ ，其中x为不等式组 ${\begin{cases} x > - 1 \\ \frac{x - 1}{2} \leq \frac{x}{3} \end{cases}$ 的整数解.

查看试题解析
23. 如图，在△ABC中，∠BAC的平分线与BC的中垂线DE交于点E，过点E作AC边的垂线，垂足为N，过点E作AB延长线的垂线，垂足为M.

(1)、求证：BM=CN；

(2)、若，AB=2，AC=8，求BM的长.

查看试题解析
24. 某学校计划购买若干台电脑，现从甲、乙两家商场了解到同一型号电脑每台报价均为6000
元，并且多买都有一定的优惠．各商场的优惠条件如下表所示：

商场

优惠条件

甲商场

第一台按原价收费，其余每台优惠25%

乙商场

每台优惠20%

(1)、分别写出甲、乙两商场的收费y(元)与所买电脑台数x之间的关系式；

(2)、什么情况下到甲、乙两商场购买更优惠？什么情况下两家商场的收费相同？

查看试题解析
25. 如图，在△ABC中，AB=AC=4，∠BAC=120°，AD为BC边上的高，点P从点B以每秒 $\sqrt{3}$ 个单位长度的速度向终点C运动，同时点Q从点C以每秒1个单位长度的速度向终点A运动，其中一个点到达终点时，两点同时停止.

(1)、求BC的长；

(2)、设△PDQ的面积为S，点P的运动时间为t秒，求S与t的函数关系式，并写出自变量的取值范围；

(3)、在动点P、Q的运动过程中，是否存在PD=PQ，若存在，求出△PDQ的周长，若不存在，请说明理由.

查看试题解析
26. 为了全面推进素质教育，增强学生体质，丰富校园文化生活，高新区某校将举行春季特色运动会，需购买A，B两种奖品.经市场调查，若购买A种奖品3件和B种奖品2件，共需60元；若购买A种奖品1件和B种奖品3件，共需55元．

(1)、求A、B两种奖品的单价各是多少元；

(2)、运动会组委会计划购买A、B两种奖品共100件，购买费用不超过1160元，且A种奖品的数量不大于B种奖品数量的3倍，运动会组委会共有几种购买方案？

(3)、在第(2)问的条件下，设计出购买奖品总费用最少的方案,并求出最小总费用.

查看试题解析
27. 在△OAB中，OA=OB，∠AOB=30°，将△OAB绕点O顺时针旋 $β$ °( $30 < β < 150$ )转至△OCD，点A、B的对应点分别为C、D，连接BD、AC，线段BD与线段AC交于点M，连接OM.

(1)、如图，求证AC=BD；

(2)、如图，求证OM平分∠AMD；

(3)、如图，若 $β$ =90，AO= $2 \sqrt{3} + 2$ ，求CM的长.

查看试题解析

商场	优惠条件
甲商场	第一台按原价收费，其余每台优惠25%
乙商场	每台优惠20%