山西省吕梁市交城县2018-2019学年八年级下学期数学期中考试试卷
试卷更新日期:2020-03-05 类型:期中考试
一、单选题
-
1. 若二次根式 有意义,则
 的取值范围是( ) A、x>2 B、x<2 C、x≥2 D、x≤22. 已知 ABCD中,∠A+∠C=200°,则∠B的度数是( )A、100° B、160° C、80° D、60°3. 下列计算正确是A、 B、 C、 D、4. 下列各组数中,以它们为边长的线段不能构成直角三角形的是( )A、1,
的取值范围是( ) A、x>2 B、x<2 C、x≥2 D、x≤22. 已知 ABCD中,∠A+∠C=200°,则∠B的度数是( )A、100° B、160° C、80° D、60°3. 下列计算正确是A、 B、 C、 D、4. 下列各组数中,以它们为边长的线段不能构成直角三角形的是( )A、1,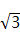 ,2
B、1,2,
,2
B、1,2, 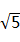 C、5,12,13
D、1,
C、5,12,13
D、1, 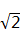 ,
, 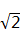 5. 如图,在▱ABCD中,CE⊥AB,垂足为点E,若∠A=130°,则∠BCE等于( )
5. 如图,在▱ABCD中,CE⊥AB,垂足为点E,若∠A=130°,则∠BCE等于( )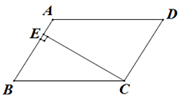 A、30° B、40° C、50° D、45°6. 已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )
A、30° B、40° C、50° D、45°6. 已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( ) A、OE= DC B、OA=OC C、∠BOE=∠OBA D、∠OBE=∠OCE7. 3世纪我国汉代的数学家赵爽在注解一部数学著作时,创作了一幅“弦图”,叫做“赵爽弦图”,并用数形结合的方法,给出了勾股定理的详细证明.这部中国古代数学著作是( )A、《周髀算经》 B、《九章算术》 C、《孙子算经》 D、《海岛算经》8. 下列命题中,真命题是( )A、有两边相等的平行四边形是菱形 B、有一个角是直角的四边形是矩形 C、四个角相等的菱形是正方形 D、两条对角线互相垂直且相等的四边形是正方形9. 如图,AB=BC=CD=DE=1,AB⊥BC,AC⊥CD,AD⊥DE,则AE=( )
A、OE= DC B、OA=OC C、∠BOE=∠OBA D、∠OBE=∠OCE7. 3世纪我国汉代的数学家赵爽在注解一部数学著作时,创作了一幅“弦图”,叫做“赵爽弦图”,并用数形结合的方法,给出了勾股定理的详细证明.这部中国古代数学著作是( )A、《周髀算经》 B、《九章算术》 C、《孙子算经》 D、《海岛算经》8. 下列命题中,真命题是( )A、有两边相等的平行四边形是菱形 B、有一个角是直角的四边形是矩形 C、四个角相等的菱形是正方形 D、两条对角线互相垂直且相等的四边形是正方形9. 如图,AB=BC=CD=DE=1,AB⊥BC,AC⊥CD,AD⊥DE,则AE=( )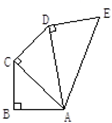 A、1 B、 C、 D、210. 如图,将长方形ABCD沿直线EF折叠,使顶点C恰好落在顶点A处,已知AB=4cm,AD=8cm,则折痕EF的长为( )
A、1 B、 C、 D、210. 如图,将长方形ABCD沿直线EF折叠,使顶点C恰好落在顶点A处,已知AB=4cm,AD=8cm,则折痕EF的长为( )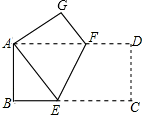 A、5cm B、 cm C、 cm D、 cm
A、5cm B、 cm C、 cm D、 cm二、填空题
-
11. 计算: = .12. 如图,平行四边形ABCD的对角线AC,BD相交于点O,请你添加一个适当的条件使其成为菱形(只填一个即可).
 13. 如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,AD⊥BC于点D,则AD的长为.
13. 如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,AD⊥BC于点D,则AD的长为. 14. 如图,AB是池塘两端,设计一方案测量AB的距离,首先取一点C,连接AC,BC,再取它们的中点D,E,测得DE=15米,则AB=米.
14. 如图,AB是池塘两端,设计一方案测量AB的距离,首先取一点C,连接AC,BC,再取它们的中点D,E,测得DE=15米,则AB=米.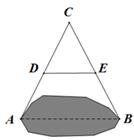 15. 如图,在菱形ABCD中,对角线AC=6,AB=5,则菱形ABCD的面积为.
15. 如图,在菱形ABCD中,对角线AC=6,AB=5,则菱形ABCD的面积为.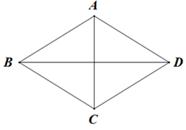 16. 计算: = .17.
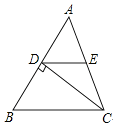
16. 计算: = .17.如图,△ABC中,CD⊥AB于D,E是AC的中点.若AD=6,DE=5,则CD的长等于
 18. 如图,在正方形ABCD中,O是对角线AC,BD的交点,过点O作OE⊥OF,分别交AB,BC于点E,F,若AE=4,CF=3,则四边形OEBF的面积为.
18. 如图,在正方形ABCD中,O是对角线AC,BD的交点,过点O作OE⊥OF,分别交AB,BC于点E,F,若AE=4,CF=3,则四边形OEBF的面积为.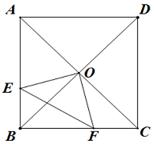
三、解答题
-
19. 计算:(1)、(2)、20. 如图都是由边长为1的小正方形组成的网格图,小正方形的顶点称为格点.请按下列要求作图.
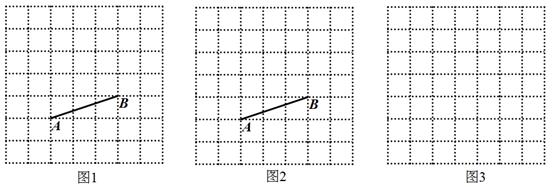 (1)、在图1中,已知线段AB,再作一条端点在格点上的线段CD= ,并且使CD⊥AB;(2)、在图2中,已知线段AB,以线段AB为边作一个格点菱形ABCD;(3)、在图3中,作一幅“赵爽弦图”.21. 如图,已知D是△ABC的边AB上一点,CE∥AB,DE交AC于点O, 且OA=OC,猜想线段CD与线段AE的大小关系和位置关系,并加以证明.
(1)、在图1中,已知线段AB,再作一条端点在格点上的线段CD= ,并且使CD⊥AB;(2)、在图2中,已知线段AB,以线段AB为边作一个格点菱形ABCD;(3)、在图3中,作一幅“赵爽弦图”.21. 如图,已知D是△ABC的边AB上一点,CE∥AB,DE交AC于点O, 且OA=OC,猜想线段CD与线段AE的大小关系和位置关系,并加以证明.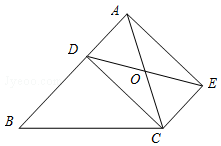 22. 阅读材料,并完成相应任务.
22. 阅读材料,并完成相应任务.2000多年来,人们对勾股定理的证明颇感兴趣,不但因为这个定理重要、基本,还因为这个定理贴近人们的生活实际,所以很多人都探讨、研究它的证明,新的证法不断出现.
下面的图形是传说中毕达哥拉斯的证明图形:
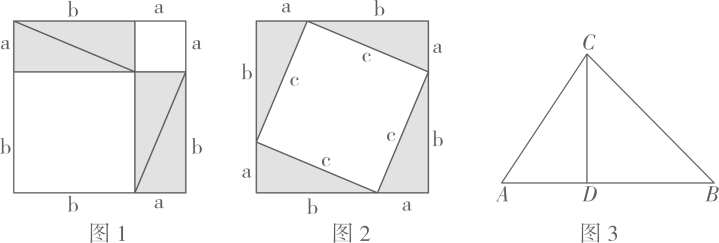 (1)、证明:①在图1中,∵
(1)、证明:①在图1中,∵4个直角三角形的面积+两个正方形的面积
=4×++ .
②在图2中,∵
4个直角三角形的面积+正方形的面积
=4×+.
∴4× + + =4×+ .
整理得:
∴ .
任务:将材料中的空缺部分补充完整;
(2)、如图3,在△ABC中,∠A=60°,∠ACB=75°,CD⊥AB,AC=4,求BC的长.23.(1)、如图1,四边形ABCD是正方形,G是BC上的任意一点,DE⊥AG,BF⊥AG,垂足分别为点E,F.求证: ;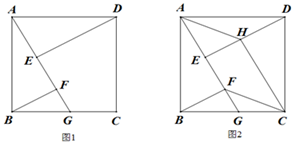 (2)、在图1的基础上,若过点C作CH⊥DE,垂足为点H,连接AH,CF,如图2.求证:四边形AFCH为平行四边形.24. 实践与探究
(2)、在图1的基础上,若过点C作CH⊥DE,垂足为点H,连接AH,CF,如图2.求证:四边形AFCH为平行四边形.24. 实践与探究在综合实践课上,老师让同学们以两个全等的三角形纸片为操作对象,进行相关问题的探究.如图1,△ABC≌△DEF,其中∠ACB=90°,∠A=30°,AB=4.
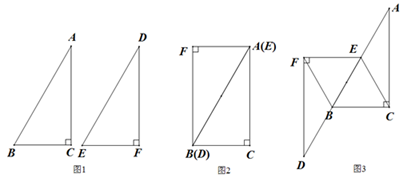 (1)、请直接写出EF=;(2)、新星小组将这两张纸片按如图2所示的方式放置后,经过观察发现四边形ACBF是矩形,请你证明这个结论.(3)、新星小组在图2的基础上,将△DEF纸片沿AB方向平移至如图3的位置,其中点E与AB的中点重合,连接CE,BF.请你判断四边形BCEF的形状,并证明你的结论.
(1)、请直接写出EF=;(2)、新星小组将这两张纸片按如图2所示的方式放置后,经过观察发现四边形ACBF是矩形,请你证明这个结论.(3)、新星小组在图2的基础上,将△DEF纸片沿AB方向平移至如图3的位置,其中点E与AB的中点重合,连接CE,BF.请你判断四边形BCEF的形状,并证明你的结论.