山西省晋中市灵石县2017-2018学年八年级下学期数学期中考试试卷

试卷更新日期：2020-03-05 类型：期中考试

进入出卷网下载

一、单选题

1. 将分式 $\frac{x y}{x - y} (x \neq 0, y \neq 0)$ 中的 $x$ . $y$ 扩大为原来的3倍，则分式的值为：（）

A、不变； B、扩大为原来的3倍 C、扩大为原来的9倍； D、减小为原来的 $\frac{1}{3}$

查看试题解析
2. 下列图形中，既是轴对称图形又是中心对称图形的是 $($ 　　 $)$

A、 B、 C、 D、

查看试题解析
3. 下列从左到右的变形，是分解因式的为（）

A、x²－x=x(x－1) B、a(a－b)=a²－ab C、(a+3)(a－3)=a²－9 D、x²－2x+1=x(x－2)+1

查看试题解析
4. 已知：直线AB和AB外一点C（图3-45）．
作法：(1)任意取一点K，使K和C在AB的两旁．

⑵以C为圆心，CK长为半径作弧，交AB于点D和E．

⑶分别以D和E为圆心，大于 $\frac{1}{2}$ DE的长为半径作弧，两弧交于点F．

⑷作直线CF．直线CF就是所求的垂线．

这个作图是（）

A、平分已知角 B、作一个角等于已知角 C、过直线上一点作此直线的垂线 D、过直线外一点作此直线的垂线

查看试题解析
5. 下列分式中，最简分式是（）

A、 $\frac{x - y}{y - x}$ B、 $\frac{x + 1}{x^{2} - 1}$ C、 $\frac{x^{2} - 1}{x^{2} + 1}$ D、 $\frac{x^{2} - 4}{2 x + 4}$

查看试题解析
6. 如图，两只蚂蚁以相同的速度沿两条不同的路径，同时从A出发爬到B，则（）

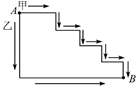A、乙比甲先到 B、甲和乙同时到 B． C、甲比乙先到 D、无法确定

查看试题解析
7. 给出下面两个定理：
①线段垂直平分线上的点到这条线段两个端点的距离相等；

②到一条线段两个端点距离相等的点在这条线段的垂直平分线上.

应用上述定理进行如下推理：

如图，直线l是线段MN的垂直平分线.

∵点A在直线l上，∴AM=AN.(　　)

∵BM=BN，∴点B在直线l上.(　　)

∵CM≠CN，∴点C不在直线l上.

这是∵如果点C在直线l上，那么CM=CN， (　　)

这与条件CM≠CN矛盾.

以上推理中各括号内应注明的理由依次是 (　　)

A、②①① B、②①② C、①②② D、①②①

查看试题解析
8. 如图所示，在Rt△ACD和Rt△BCE中，若AD＝BE，DC＝EC，则无法得出的结论是（　　）

A、OA＝OB B、E是AC的中点 C、△AOE≌△BOD D、AE＝BD

查看试题解析
9. 如图，△DEF是由△ABC绕着某点旋转得到的，则这点的坐标是（）

A、（1，1） B、（0，1） C、（﹣1，1） D、（2，0）

查看试题解析
10. 在等边三角形ABC中，D，E分别是BC，AC的中点，点P是线段AD上的一个动点，当△PCE的周长最小时，P点的位置在（）．

A、A点处 B、D点处 C、AD的中点处 D、△ABC三条高线的交点处

查看试题解析

二、填空题

11. 一个正方形的面积是（a²+8a+16）cm² ，则此正方形的边长是cm．

查看试题解析
12. 当x时，分式 $\frac{| x | - 3}{x - 3}$ 的值为零．

查看试题解析
13. 如图，点P是∠AOB的角平分线上一点，过点P作PC∥OA交OB于点C，过点P作PD⊥OA于点D，若∠AOB＝60°，OC＝4，则PD＝．

查看试题解析
14. 化简： $\frac{a^{2} - 1}{a^{2}}$ ÷（ $\frac{1}{a}$ ﹣1）•a＝．

查看试题解析
15. 如图，在Rt△ABC中，AB＝AC，D、E是斜边BC上两点，且∠DAE＝45°，将△ABE绕点A顺时针旋转90°后，得到△ACF，连接DF，下列结论中：①∠DAF=45°②△ABE≌△ACD③AD平分∠EDF④BE²+DC²＝DE²；
正确有（填序号）

查看试题解析

三、解答题

16.

(1)、解不等式组，并在数轴上表示出解集：
① ${\begin{array}{l} 8 x + 5 > 9 x + 6 \\ 2 x - 1 < 7 \end{array}$

② ${\begin{array}{l} \frac{2 x - 1}{3} - \frac{5 x + 1}{2} \leq 1 \\ 5 x - 1 < 3 (x + 1) \end{array}$

(2)、分解因式：
①x（x﹣y）﹣y（y﹣x）

②﹣12x³+12x²y﹣3xy² ．

查看试题解析
17.

(1)、计算： ${(\frac{b}{2 a x})}^{2} \div (- \frac{a x}{3 b}) \times \frac{8 a}{b^{3}}$

(2)、先化简，再求值： $(\frac{1}{a - 2} + \frac{1}{a + 2}) \div \frac{2 a}{a + 2}$ ，其中a＝2﹣ $\sqrt{2}$ ．

查看试题解析
18. 作图题：如图，在边长为1的正方形网格中，△ABC的三个顶点和点D都在小方格的顶点上，请按要求作图.

(1)、平移△ABC，使点A平移到点D，得到△DEF；

(2)、请写出第（1）小题平移的过程.

查看试题解析
19. 分解因式x²－4y²－2x＋4y，细心观察这个式子就会发现，前两项符合平方差公式，后两项可提取公因式，前后两部分分别分解因式后会产生公因式，然后提取公因式就可以完成整个式子的分解因式，过程为：x²－4y²－2x＋4y＝(x＋2y)(x－2y)－2(x－2y)＝(x－2y)(x＋2y－2)．这种分解因式的方法叫分组分解法，利用这种方法解决下列问题：

(1)、分解因式：a²－4a－b²＋4；

(2)、若△ABC三边a、b、c满足a²－ab－ac＋bc＝0，试判断△ABC的形状．

查看试题解析
20. 如图，△ABC为等边三角形，∠BAD=∠ACF=∠CBE，求∠DEC的度数。

查看试题解析
21. 如图，小明的家位于一条南北走向的河流MN的东侧A处，某一天小明从家出发沿南偏西30°方向走60m到达河边B处取水，然后沿另一方向走80m到达菜地C处浇水，最后沿第三方向走100m回到家A处．问小明在河边B处取水后是沿哪个方向行走的？并说明理由．

查看试题解析
22. 数学活动问题情境：
如图1，在△ABC中，AB＝AC，∠BAC＝90°，D，E分别是边AB，AC的中点，将△ADE绕点A顺时针旋转α角（0°＜α＜90°）得到△AD′E′，连接CE′，BD′．探究CE′与BD′的数量关系；

探究发展：

(1)、图1中，猜想CE′与BD′的数量关系，并证明；

(2)、如图2，若将问题中的条件“D，E分别是边AB，AC的中点”改为“D为AB边上任意一点，DE∥BC交AC于点E“，其他条件不变，（1）中CE′与BD′的数量关系还成立吗？请说明理由；
拓展延伸：

(3)、如图3，在△ABC中，AB＝AC，∠BAC＝60°，点D，E分别在AB，AC上，且DE∥BC，将△ADE绕点A顺时针旋转60°得到△AD′E′，连接CE′，BD′，请你仔细观察，提出一个你最关心的数学问题（例如：CE′与BD′相等吗？）．

查看试题解析
23. 如图，在Rt△ABC，∠ABC=90°，AB=20，BC=15，点D为AC边上的动点，点D从点C出发，沿CA往A运动，当运动到点A时停止.若设点D的运动时间为t秒，点D运动的速度为每秒2个单位长度.

(1)、当t=2时，求CD、AD的长；

(2)、在D运动过程中，△CBD能否为直角三角形，若不能，请说明理由，若能，请求出t的值；

(3)、当t为何值时，△CBD是等腰三角形，请直接写出t的值.

查看试题解析