湖北省武汉市江岸区2019年数学中考模拟试卷
试卷更新日期:2020-03-05 类型:中考模拟
一、单选题
-
1. 将方程x2-8x=10化为一元二次方程的一般形式,其中一次项系数、常数项分别是( )A、-8、-10 B、-8、10 C、8、-10 D、8、102. 下列图形中,可以看作是中心对称图形的是( )A、
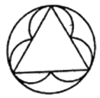 B、
B、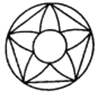 C、
C、 D、
D、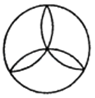 3. 下列事件中,是确定事件的是( )A、度量三角形的内角和,结果是 B、买一张电影票,座位号是奇数 C、打开电视机,它正在播放花样滑冰 D、明天晚上会看到月亮4. 如图,PA,PB切⊙O于点A,B,点C是⊙O上一点,且∠P=36°,则∠ACB=( )
3. 下列事件中,是确定事件的是( )A、度量三角形的内角和,结果是 B、买一张电影票,座位号是奇数 C、打开电视机,它正在播放花样滑冰 D、明天晚上会看到月亮4. 如图,PA,PB切⊙O于点A,B,点C是⊙O上一点,且∠P=36°,则∠ACB=( )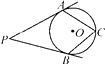 A、54° B、72° C、108° D、144°5. 如图,一个圆形转盘被平均分成6个全等的扇形,任意旋转这个转盘1次,则当转盘停止转动时,指针指向阴影部分的概率是( )
A、54° B、72° C、108° D、144°5. 如图,一个圆形转盘被平均分成6个全等的扇形,任意旋转这个转盘1次,则当转盘停止转动时,指针指向阴影部分的概率是( )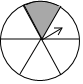 A、 B、 C、 D、6. 我市某楼盘准备以每平方米6000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,为了加快资金周转,房地产开发商对价格经过连续两次下调后,决定以每平方米4860元的均价开盘销售,则平均每次下调的百分率是( )。
A、 B、 C、 D、6. 我市某楼盘准备以每平方米6000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,为了加快资金周转,房地产开发商对价格经过连续两次下调后,决定以每平方米4860元的均价开盘销售,则平均每次下调的百分率是( )。
A、8% B、9% C、10% D、11%7. 抛物线 的顶点坐标是( )A、(﹣1,2) B、(﹣1,﹣2) C、(1,﹣2) D、(1,2)8. 方程x2﹣8x=﹣16的根的情况是( )A、只有一个实数根 B、有两个不相等的实数根 C、有两个相等的实数根 D、没有实数根9. 已知点 , , 是抛物线 上的三点,则a,b,c的大小关系为( )A、 B、 C、 D、10. 若一个圆锥的底面半径为2cm,高为4 cm,则圆锥的侧面展开图中圆心角的度数为( )A、80° B、100° C、120° D、150°二、填空题
-
11. 在平面直角坐标系中,点P(-5,3)关于原点对称点P′的坐标是.12. 将抛物线y=x2+2x向右平移1个单位后的解析式为.13. 有四张背面完全相同的卡片,正面上分别标有数字﹣2,﹣1,1,2.把这四张卡片背面朝上,随机抽取一张,记下数字为m;放回搅匀,再随机抽取一张卡片,记下数字为n,则y=mx+n不经过第三象限的概率为.14. 某村种的水稻前年平均每公顷产7200千克,今年平均每公顷产8450千克,设这两年该村每公顷产量的年平均增长率为x,根据题意,所列方程为.15. ⊙O的内接正三角形的边长记为a3 , ⊙O的内接正方形的边长记为a4 , 则 等于.16. 已知直线 与抛物线 交于A ,B 两点,则 .
三、解答题
-
17. 已知关于x的一元二次方程:x2+ax﹣5=0的一个根是1,求a的值及该方程的另一根.18. 一只不透明的袋子中,装有2个白球和1个红球,这些球除颜色外都相同.(1)、小明认为,搅匀后从中任意摸出一个球,不是白球就是红球是等可能的,你同意他的说法吗?为什么?(2)、搅匀后从中一把摸出两个球,请通过列表和树状图求出两个球都是白球的概率.19. 如图,AB是⊙O的直径,AC是弦,D是弧BC的中点,过点D作EF垂直于直线AC,垂足为F,交AB的延长线于点E.
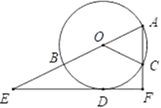 (1)、求证:EF是⊙O的切线;(2)、若AF=6,EF=8,求⊙O的半径.20. (操作发现)
(1)、求证:EF是⊙O的切线;(2)、若AF=6,EF=8,求⊙O的半径.20. (操作发现)如图①,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.
 (1)、请按要求画图:将△ABC绕点A按顺时针方向旋转90°,点B的对应点为B′,点C的对应点为C′,连接BB′;(2)、在(1)所画图形中,∠AB′B=.(3)、如图②,在等边三角形ABC中,AC=7,点P在△ABC内,且∠APC=90°,∠BPC=120°,求△APC的面积.
(1)、请按要求画图:将△ABC绕点A按顺时针方向旋转90°,点B的对应点为B′,点C的对应点为C′,连接BB′;(2)、在(1)所画图形中,∠AB′B=.(3)、如图②,在等边三角形ABC中,AC=7,点P在△ABC内,且∠APC=90°,∠BPC=120°,求△APC的面积.小明同学通过观察、分析、思考,对上述问题形成了如下想法:
想法一:将△APC绕点A按顺时针方向旋转60°,得到△AP′B,连接PP′,寻找PA,PB,PC三条线段之间的数量关系;
想法二:将△APB绕点A按逆时针方向旋转60°,得到△AP′C′,连接PP′,寻找PA,PB,PC三条线段之间的数量关系.…
请参考小明同学的想法,完成该问题的解答过程.(一种方法即可)
21. 某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:售价x(元/千克)
50
60
70
销售量y(千克)
100
80
60
(1)、求y与x之间的函数表达式;(2)、设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入﹣成本);并求出售价为多少元时获得最大利润,最大利润是多少?22. 某商店购进一批成本为每件30元的商品,商店按单价不低于成本价,且不高于50元销售.经调查发现,该商品每天的销售量y(件)与销售单价x(元)之间满足一次函数关系,其图象如图所示.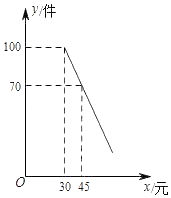 (1)、求该商品每天的销售量y(件)与销售单价x(元)之间的函数关系式;(2)、销售单价定为多少元时,才能使销售该商品每天获得的利润w(元)最大?最大利润是多少?(3)、若商店要使销售该商品每天获得的利润高于800元,请直接写出每天的销售量y(件)的取值范围.23. 如图 中, ,P是斜边AC上一个动点,以即为直径作 交BC于点D,与AC的另一个交点E,连接DE.
(1)、求该商品每天的销售量y(件)与销售单价x(元)之间的函数关系式;(2)、销售单价定为多少元时,才能使销售该商品每天获得的利润w(元)最大?最大利润是多少?(3)、若商店要使销售该商品每天获得的利润高于800元,请直接写出每天的销售量y(件)的取值范围.23. 如图 中, ,P是斜边AC上一个动点,以即为直径作 交BC于点D,与AC的另一个交点E,连接DE.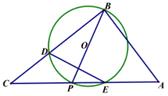
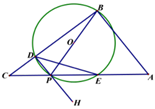 (1)、当 时,
(1)、当 时,①若 ,求 的度数;
②求证 ;
(2)、当 , 时,①是含存在点P,使得 是等腰三角形,若存在求出所有符合条件的CP的长;
②以D为端点过P作射线DH,作点O关于DE的对称点Q恰好落在 内,则CP的取值范围为
24. 抛物线y=ax2+bx+3经过点A(﹣1,0),B(3,0),与y轴交于点C.点D(xD , yD)为抛物线上一个动点,其中1<xD<3.连接AC,BC,DB,DC.(1)、求该抛物线的解析式;(2)、当△BCD的面积等于△AOC的面积的2倍时,求点D的坐标;(3)、在(2)的条件下,若点M是x轴上一动点,点N是抛物线上一动点,试判断是否存在这样的点M,使得以点B,D,M,N为顶点的四边形是平行四边形.若存在,求出点M的坐标;若不存在,请说明理由.