湖北省武汉市2020年数学中考模拟试卷
试卷更新日期:2020-03-05 类型:中考模拟
一、单选题
-
1. 方程4x2=81的一次项系数为( )
A、4 B、0 C、81 D、﹣812. 抛物线 y=(x﹣1)2﹣2 的顶点是( )A、(1,﹣2) B、(﹣1,2) C、(1,2) D、(﹣1,﹣2)3. 下列事件是必然事件的是( )A、某种彩票中奖率为1%,则买100张这种彩票必然中奖 B、今晚努力学习,明天考试必然考出好成绩 C、从装有2个红球、3个白球的袋中随机摸出4个球,则一定会摸出红球 D、抛掷一枚普通的骰子所得的点数一定小于64. 下列我国著名企业商标图案中,是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮感染后就会有100被感染.设每轮感染中平均每一台电脑会感染x台其他电脑,由题意列方程应为( )A、1+2x=100 B、x(1+x)=100 C、(1+x)2=100 D、1+x+x2=1006. 将一个球竖直向上抛起,球升到最高点,垂直下落,直到地面.在此过程中,球的高度与下落时间的关系可以用下图中的哪一幅来近似地刻画( )A、
5. 某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮感染后就会有100被感染.设每轮感染中平均每一台电脑会感染x台其他电脑,由题意列方程应为( )A、1+2x=100 B、x(1+x)=100 C、(1+x)2=100 D、1+x+x2=1006. 将一个球竖直向上抛起,球升到最高点,垂直下落,直到地面.在此过程中,球的高度与下落时间的关系可以用下图中的哪一幅来近似地刻画( )A、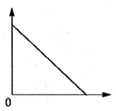 B、
B、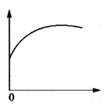 C、
C、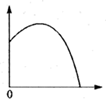 D、
D、 7. 某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图所示),并规定:顾客消费200元以上(含200元),就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准九折、八折、七折区域,顾客就可以获得此项优惠,如果指针恰好在分界线上时,则需要重新转动转盘.某顾客正好消费300元,他转动一次转盘,实际付款210元的概率为( )
7. 某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图所示),并规定:顾客消费200元以上(含200元),就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准九折、八折、七折区域,顾客就可以获得此项优惠,如果指针恰好在分界线上时,则需要重新转动转盘.某顾客正好消费300元,他转动一次转盘,实际付款210元的概率为( ) A、 B、 C、 D、8. 如图,在Rt△ABC中,∠ACB=90°,AC=BC,将△ABC绕点A逆时针旋转60°,得到△ADE,连接BE,则∠BED的度数为( )
A、 B、 C、 D、8. 如图,在Rt△ABC中,∠ACB=90°,AC=BC,将△ABC绕点A逆时针旋转60°,得到△ADE,连接BE,则∠BED的度数为( )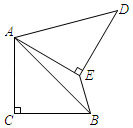 A、100° B、120° C、135° D、150°9. 抛物线y=mx2+3mx+2(m<0)经过点A(a,y1)、B(1,y2)两点,若y1>y2 , 则实数a满足( )A、﹣4<a<1 B、a<﹣4或a>1 C、﹣4<a≤﹣ D、﹣ ≤a<110. 如图,△ABC内接于⊙O,AC=5,BC=12,且∠A=90°+∠B,则点O到AB的距离为( )
A、100° B、120° C、135° D、150°9. 抛物线y=mx2+3mx+2(m<0)经过点A(a,y1)、B(1,y2)两点,若y1>y2 , 则实数a满足( )A、﹣4<a<1 B、a<﹣4或a>1 C、﹣4<a≤﹣ D、﹣ ≤a<110. 如图,△ABC内接于⊙O,AC=5,BC=12,且∠A=90°+∠B,则点O到AB的距离为( )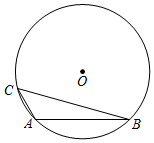 A、 B、 C、 D、4
A、 B、 C、 D、4二、填空题
-
11. 一元二次方程x(x﹣5)=0的根为.12. 把点P(﹣2,3)绕坐标原点旋转180°后对应点的坐标为.13. 抛物线y=x2﹣2x﹣5的顶点坐标是.14. 如图,扇形的弧长是 ,面积是 ,则此扇形的圆心角的度数是.
 15. 已知抛物线y=ax2+bx+c经过点(﹣1,5),且无论m为何值,不等式a+b≥am2+bm恒成立,则关于x的方程ax2+bx+c=5的解为.16. 平面直角坐标系中,点P是一动点,点A(6,0)绕点P顺时针旋转90°到点B处,点B恰好落在直线y=﹣2x上.当线段AP最短时,点P的坐标为.
15. 已知抛物线y=ax2+bx+c经过点(﹣1,5),且无论m为何值,不等式a+b≥am2+bm恒成立,则关于x的方程ax2+bx+c=5的解为.16. 平面直角坐标系中,点P是一动点,点A(6,0)绕点P顺时针旋转90°到点B处,点B恰好落在直线y=﹣2x上.当线段AP最短时,点P的坐标为.三、解答题
-
17. 解方程:x2﹣4x﹣7=0.18. 如图,A、B是⊙O上的两点,∠AOB=120°,C是弧AB的中点,CE⊥OA交⊙O于点E,连接AE.求证:AE=AO.
 19. 为了有效保护环境,某景区要求游客将垃圾按可回收垃圾,不可回收垃圾,有害垃圾分类投放.一天,小林一家游玩了该景区后,把垃圾按要求分成三袋并随机投入三类垃圾桶中,请用列树状图的方法求三袋垃圾都投对的概率.20. 在正方形ABCD中,E为AB的中点.
19. 为了有效保护环境,某景区要求游客将垃圾按可回收垃圾,不可回收垃圾,有害垃圾分类投放.一天,小林一家游玩了该景区后,把垃圾按要求分成三袋并随机投入三类垃圾桶中,请用列树状图的方法求三袋垃圾都投对的概率.20. 在正方形ABCD中,E为AB的中点. (1)、将线段AB绕点O逆时针旋转一定角度,使点A与点B重合,点B与点C重合,用无刻度直尺作出点O的位置,保留作图痕迹;(2)、将△ABD绕点D逆时针旋转某个角度,得到△CFD,使DA与DC重合,用无刻度直尺作出△CFD,保留作图痕迹.21. 如图,在⊙O中,AB为直径,F是半圆弧AB的中点,E是弧BF上一点,直线AE与过点B的切线相交于点C,连接EF.
(1)、将线段AB绕点O逆时针旋转一定角度,使点A与点B重合,点B与点C重合,用无刻度直尺作出点O的位置,保留作图痕迹;(2)、将△ABD绕点D逆时针旋转某个角度,得到△CFD,使DA与DC重合,用无刻度直尺作出△CFD,保留作图痕迹.21. 如图,在⊙O中,AB为直径,F是半圆弧AB的中点,E是弧BF上一点,直线AE与过点B的切线相交于点C,连接EF. (1)、若EF= AB,求∠ACB的度数;(2)、若⊙O的半径为3,BC=2,求EF的长.22. 某坦克部队需要经过一个拱桥(如图所示),拱桥的轮廓是抛物线形,拱高OC=6m,跨度AB=20m,有5根支柱:AG、MN、CD、EF、BH,相邻两支柱的距离均为5m.
(1)、若EF= AB,求∠ACB的度数;(2)、若⊙O的半径为3,BC=2,求EF的长.22. 某坦克部队需要经过一个拱桥(如图所示),拱桥的轮廓是抛物线形,拱高OC=6m,跨度AB=20m,有5根支柱:AG、MN、CD、EF、BH,相邻两支柱的距离均为5m.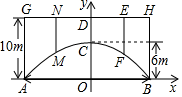 (1)、以AB的中点为原点,AB所在直线为x轴,支柱CD所在直线为y轴,建立平面直角坐标系,求抛物线的解析式;(2)、若支柱每米造价为2万元,求5根支柱的总造价;(3)、拱桥下面是双向行车道(正中间是一条宽2m的隔离带),其中的一条行车道是坦克的行进方向,现每辆坦克长4m,宽2m,高3m,行驶速度为24km/h,坦克允许并排行驶,坦克前后左右距离忽略不计,试问120辆该型号坦克从刚开始进入到全部通过这座长1000m的拱桥隧道所需最短时间为多少分钟?23. 已知平行四边形ABCD.
(1)、以AB的中点为原点,AB所在直线为x轴,支柱CD所在直线为y轴,建立平面直角坐标系,求抛物线的解析式;(2)、若支柱每米造价为2万元,求5根支柱的总造价;(3)、拱桥下面是双向行车道(正中间是一条宽2m的隔离带),其中的一条行车道是坦克的行进方向,现每辆坦克长4m,宽2m,高3m,行驶速度为24km/h,坦克允许并排行驶,坦克前后左右距离忽略不计,试问120辆该型号坦克从刚开始进入到全部通过这座长1000m的拱桥隧道所需最短时间为多少分钟?23. 已知平行四边形ABCD. (1)、如图1,将▱ABCD绕点D逆时针旋转一定角度得到▱A1B1C1D,延长B1C1 , 分别与BC、AD的延长线交于点M、N.
(1)、如图1,将▱ABCD绕点D逆时针旋转一定角度得到▱A1B1C1D,延长B1C1 , 分别与BC、AD的延长线交于点M、N.①求证:∠BMB1=∠ADA1;
②求证:B1N=AN+C1M;
(2)、如图2,将线段AD绕点D逆时针旋转,使点A的对应点A1落在BC上,将线段CD绕点D逆时针旋转到C1D的位置,AC1与A1D交于点H.若H为AC1的中点,∠ADC1+∠A1DC=180°,A1B=nA1C,试用含n的式子表示 的值.24. 已知抛物线y=x2+(2m﹣1)x﹣2m(m>0.5)的最低点的纵坐标为﹣4.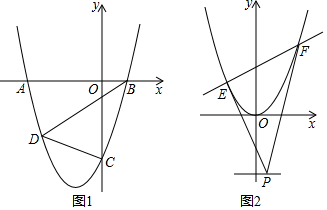 (1)、求抛物线的解析式;(2)、如图1,抛物线与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,D为抛物线上的一点,BD平分四边形ABCD的面积,求点D的坐标;(3)、如图2,平移抛物线y=x2+(2m﹣1)x﹣2m,使其顶点为坐标原点,直线y=﹣2上有一动点P,过点P作两条直线,分别与抛物线有唯一的公共点E、F(直线PE、PF不与y轴平行),求证:直线EF恒过某一定点.
(1)、求抛物线的解析式;(2)、如图1,抛物线与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,D为抛物线上的一点,BD平分四边形ABCD的面积,求点D的坐标;(3)、如图2,平移抛物线y=x2+(2m﹣1)x﹣2m,使其顶点为坐标原点,直线y=﹣2上有一动点P,过点P作两条直线,分别与抛物线有唯一的公共点E、F(直线PE、PF不与y轴平行),求证:直线EF恒过某一定点.