河南省2019年普通高中招生数学模拟试卷
试卷更新日期：2020-03-05 类型：中考模拟
一、单选题
-
1. ﹣3的相反数是（ ）A、 B、 C、 D、2. 科学家可以使用冷冻电子显微镜技术以高分率测定溶液中的生物分子结构，使用此技术测定细菌蛋白结构的分辨率达到0.22nm，已知1nm＝10﹣9m，则0.22nm用科学记数法表示为（ ）A、2.2×10 m B、2.2×10 m C、0.22×10 m D、22×10 m3. 下列几何体是由5个相同的小正方体搭成的，它的左视图是（ ）
A、
B、
C、
D、
4. 如图，直线AB，CD被直线EF所截，AB∥CD，DG⊥BF于点G，若∠1＝130°，则∠2的度数为（ ）
A、25° B、30° C、35° D、40°5. 不等式组 的解集在数轴上表示为（ ）A、
B、
C、
D、
6. 在第37届中国洛阳文化节期间，某手工刺绣服装店老板某天销售了10件同款的女装上衣，销售尺码统计如下表：尺码/cm
155
160
165
170
175
销量/件
1
4
2
2
1
则这10件上衣尺码的平均数和众数分别为（ ）
A、160，164 B、160，4 C、164，160 D、164，47. 我国古代伟大的数学家刘徽将直角三角形分割成一个正方形和两对全等的直角三角形，得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理.如图，若a＝4，b＝6，则该直角三角形的周长为（ ）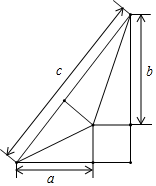
A、18 B、20 C、24 D、268. 现有四张分别标有数字﹣2，﹣1，1，3的卡片，它们除数字外完全相同，把卡片背面朝上洗匀，从中随机抽取一张卡片，记下数字后放回，洗匀，再随机抽取一张卡片，则第一次抽取的卡片上的数字大于第二次抽取的卡片上的数字的概率是（ ）A、 B、 C、 D、9. 如图，▱ABCD的对角线AC与BD相交于点O，过点O作OE⊥AD于点E，若AB＝4，∠ABC＝60°，则OE的长是（ ）
A、 B、2 C、2 D、10. 如图，点P在平面直角坐标系中按图中箭头所示的方向运动，每次运动一个单位，△A3A4A5和△A8A9A10都是等边三角形.第一次从（0，1）运动到点A1（0，2），第二次接着运动到点A2（1，2），第三次运动到点A3（1，1），…，经过2019次运动，动点P所在位置A2019的坐标是（ ）
A、（807， ） B、（ ，2﹣ ） C、（ ， ） D、（807，2﹣ ）二、填空题
-
11. 计算：（ ）0+（﹣2）2＝.12. 已知关于x的一元二次方程x2+（m+1）x+ m2+1＝0有两个相等的实数根，则m的值是.13. 二次函数 的图象上有三个点，分别为A（﹣2，y1），B（﹣1，y2），C（1，y3），则y1 ， y2 ， y3的大小关系是.14. 如图，将边长为4的正方形ABCD绕AD的中点O按逆时针方向旋转后得到正方形A′B′C′D′，当点D的对应点D′落在对角线AC上时，点C所经过的路径与CD′，C′D′所围成图形的阴影部分面积是.
15. 如图，在矩形ABCD中，AB＝4，BC＝5，E，F分别是线段CD和线段BA延长线上的动点，沿直线EF折叠使点D的对应点D′落在BC上，连接AD′，DD′，当△ADD′是以DD′为腰的等腰三角形时，DE的长为.
三、解答题
-
16. 先化简，再求值：（x+3）（x﹣3）+（2x﹣1）2﹣x（3x﹣4），其中x＝ .17. 《中国诗词大会》以“赏中华诗词，寻文化基因、品生活之美”为基本宗旨，力求通过对诗词知识的比拼及赏析，带动全民重温那些曾经学过的古诗词，分享诗词之美，感受诗词之趣，从古人的智慧和情怀中汲取营养，涵养心灵，自开播以来深受广大师生的喜爱，某中学为了解学校学生的诗词水平，从八、九年级各随机抽取了20名学生进行了测试，并将八、九年级测试成绩（百分制，单位：分）整理如下：
收集数据
八年级 93 92 84 55 85 82 66 74 88 67 87 87 67 61 87 61 78 57 72 75
九年级 68 66 79 92 86 87 61 86 90 83 90 78 70 67 53 79 86 71 61 89(1)、整理数据按如下分数段整理数据，并补全表格：测试成绩x（分）
年级
50≤x＜60
60≤x＜70
70≤x＜80
80≤x＜90
90≤x≤100
八
2
4
九
1
5
5
6
3
说明：测试成绩x（分），其中x≥80为优秀，70≤x＜80为良好，60≤x＜70为合格，0≤x＜60为不合格）
分析数据补全下列表格中的统计量：
年级
平均数
中位数
众数
八
75.9
76.5
九
77.1
79
86
(2)、得出结论：在此次测试中，有位同学的成绩是78分，在他所在的年级属于中等偏上，则这位同学属于哪个年级？
(3)、若九年级有800名学生，估计九年级诗词水平达到优秀的学生有多少名？18. 如图，AB是⊙O的直径，DC为⊙O的切线，DE⊥AB，垂足为点E，交⊙O于点F，弦AC交DE于点P，连接CF.
(1)、求证：∠DPC＝∠PCD；(2)、若AP＝2，填空：①当∠CAB＝时，四边形OBCF是菱形；
②当AC＝2AE时，OB＝.
19. 2019年4月23日是中国人民解放军海军成立70周年纪念日，届时将在青岛举行盛大的多国海军庆祝活动.为此我国海军进行了多次军事演习.如图，在某次军事演习时，舰艇A发现在他北偏东22°方向上有不明敌舰在指挥中心O附近徘徊，快速报告给指挥中心，此时在舰艇A正西方向50海里处的舰艇B接到返回指挥中心的行动指令，舰艇B迅速赶往在他北偏东60°方向的指挥中心处，舰艇B的速度是80海里/小时，请根据以上信息，求舰艇B到达指挥中心O的时间.（结果精确到0.1小时，参考数据：（sin22°≈0.37，cos22°≈0.93，tan22°≈0.40， ＝1.73）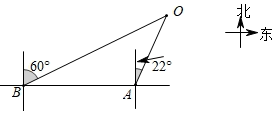
20. 如图，一次函数y＝k1x+3的图象与坐标轴相交于点A（﹣2，0）和点B，与反比例函数y＝ （x＞0）相交于点C（2，m）.
(1)、填空：k1＝ ， k2＝；(2)、若点P是反比例函数图象上的一点，连接CP并延长，交x轴正半轴于点D，若PD：CP＝1：2时，求△COP的面积.21. 某品牌的洗衣机在市场上享有美誉，市场标价为 元，进价为 元，市场调研发现，若在市场价格的基础上降价会引起销售量的增加，当销售价格为 元时，月销售量为 台；当销售价格为 元时，月销售量为 台.若月销售量 （台）与销售价格 （元）满足一次函数关系.(1)、求 与 之间的函数关系式；(2)、公司决定采取降价促销，迅速占领市场的方案，请根据以上信息，判断当销售价格 定为多少元时，公司的月利润 最大，并求出 的最大值.22. 如图
(1)、问题发现如图①，在Rt△ABC中，∠A＝90°，AB＝kAC，点D是AB上一点，DE∥BC.
填空：BD，CE的数量关系为；位置关系为；
(2)、类比探究如图②，将△ADE绕着点A顺时针旋转，旋转角为α（0°＜α≤90°），连接BD，CE，请问（1）中的结论还成立吗？若成立，请给出证明，若不成立，请说明理由.
(3)、拓展延伸在（2）的条件下，将△ADE绕点A顺时针旋转，旋转角为α，直线BD，CE交于点F，若AC＝1，AB＝ ，当∠ACE＝15°时，请直接写出BF的长.
23. 如图，已知抛物线y＝ax2+bx+5与x轴交于A（﹣1，0），B（5，0）两点（点A在点B的左侧），与y轴交于点C.
(1)、求抛物线的解析式；(2)、点D是第一象限内抛物线上的一个动点（与点C，B不重合），过点D作DF⊥x轴于点F，交直线BC于点E，连接BD，直线BC能否把△BDF分成面积之比为2：3的两部分？若能，请求出点D的坐标；若不能，请说明理由.(3)、若M为抛物线对称轴上一动点，使得△MBC为直角三角形，请直接写出点M的坐标.