海南省2020年数学中考模拟试卷
试卷更新日期:2020-03-05 类型:中考模拟
一、单选题
-
1. 生产厂家检测4个篮球的质量,结果如图所示,超过标准质量的克数记为正数,不足标准质量的克数记为负数,其中最接近标准质量的篮球是( )



 A、+2.4 B、−0.5 C、+0.6 D、−3.42. 已知 ,则代数式 的值是( )A、2 B、-2 C、-4 D、3. 下列各式中,计算正确的是( )A、a3•a2=a6 B、a3+a2=a5 C、(a3)2=a6 D、a6÷a3=a24. 方程 的解为( )A、x=﹣1 B、x=0 C、x= D、x=15. 华为Mate 30 5G系列是近期相当火爆的5G国产手机,它采用的麒麟990 5G芯片在指甲盖大小的尺寸上集成了103亿个晶体管,将103亿用科学记数法表示为( )A、1.03×109 B、10.3×109 C、1.03×1010 D、1.03×10116. 如图是某兴趣社制作的模型,则它的俯视图是( )
A、+2.4 B、−0.5 C、+0.6 D、−3.42. 已知 ,则代数式 的值是( )A、2 B、-2 C、-4 D、3. 下列各式中,计算正确的是( )A、a3•a2=a6 B、a3+a2=a5 C、(a3)2=a6 D、a6÷a3=a24. 方程 的解为( )A、x=﹣1 B、x=0 C、x= D、x=15. 华为Mate 30 5G系列是近期相当火爆的5G国产手机,它采用的麒麟990 5G芯片在指甲盖大小的尺寸上集成了103亿个晶体管,将103亿用科学记数法表示为( )A、1.03×109 B、10.3×109 C、1.03×1010 D、1.03×10116. 如图是某兴趣社制作的模型,则它的俯视图是( )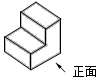 A、
A、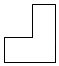 B、
B、 C、
C、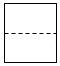 D、
D、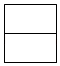 7. 已知反比例函数 的图象在每个象限内,y都随x增大而增大,则m的值可以的是 ( )A、-1 B、0 C、1 D、28. 在平面直角坐标系中,将点 向下平移2个单位长度,得到的点 的坐标为( )A、 B、 C、 D、9. 如图,ABCD为一长方形纸带,AB∥CD,将ABCD沿EF折,A,D两点分别与 对应,若∠1=2∠2,则∠AEF的度数为( )
7. 已知反比例函数 的图象在每个象限内,y都随x增大而增大,则m的值可以的是 ( )A、-1 B、0 C、1 D、28. 在平面直角坐标系中,将点 向下平移2个单位长度,得到的点 的坐标为( )A、 B、 C、 D、9. 如图,ABCD为一长方形纸带,AB∥CD,将ABCD沿EF折,A,D两点分别与 对应,若∠1=2∠2,则∠AEF的度数为( )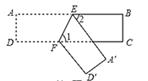 A、60° B、65° C、72° D、75°10. 在一个不透明的袋中装有10个只有颜色不同的球,其中2个红球、3个黄球和5个白球.从袋中任意摸出一个球,是白球的概率为( )A、 B、 C、 D、11. 如图,在▱ABCD中,E为边AD上的一点,将△DEC沿CE折叠至△D′EC处,若∠B=48°,∠ECD=25°,则∠D′EA的度数为( )
A、60° B、65° C、72° D、75°10. 在一个不透明的袋中装有10个只有颜色不同的球,其中2个红球、3个黄球和5个白球.从袋中任意摸出一个球,是白球的概率为( )A、 B、 C、 D、11. 如图,在▱ABCD中,E为边AD上的一点,将△DEC沿CE折叠至△D′EC处,若∠B=48°,∠ECD=25°,则∠D′EA的度数为( ) A、33° B、34° C、35° D、36°12. 如图,在Rt△ABC中,∠C=90°,点P是边AC上一点,过点P作PQ∥AB交BC于点Q,D为线段PQ的中点,BD平分∠ABC,以下四个结论①△BQD是等腰三角形;②BQ=DP;③PA= QP;④ =(1+ )2;其中正确的结论的个数( )
A、33° B、34° C、35° D、36°12. 如图,在Rt△ABC中,∠C=90°,点P是边AC上一点,过点P作PQ∥AB交BC于点Q,D为线段PQ的中点,BD平分∠ABC,以下四个结论①△BQD是等腰三角形;②BQ=DP;③PA= QP;④ =(1+ )2;其中正确的结论的个数( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
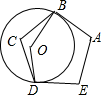
13. 因式分解: .14. 如图, 与正五边形ABCDE的边AB、DE分别相切于点B、D,则劣弧 所对的圆心角 的大小为度.
 15. 如图所示,△COD是△AOB绕点O顺时针方向旋转35°后所得的图形,点C恰好在AB上,∠AOD=90°,则∠BOC的度数是.
15. 如图所示,△COD是△AOB绕点O顺时针方向旋转35°后所得的图形,点C恰好在AB上,∠AOD=90°,则∠BOC的度数是. 16. 观察一列数:-1,2,-3,4,-5,6,-7,…,将这列数排成如图所示形式.记 对应的数为第 行第 列的数,如 ,那么 对应的数为.
16. 观察一列数:-1,2,-3,4,-5,6,-7,…,将这列数排成如图所示形式.记 对应的数为第 行第 列的数,如 ,那么 对应的数为.
三、解答题
-
17.(1)、计算:(2)、解不等式组: ,并写出它的所有整数解.18. 为建设资源节约型、环境友好型社会,切实做好节能减排工作,我市决定对居民家庭用电实行“阶梯电价”.电力公司规定:居民家庭每月用电量在80千瓦时以下(含80千瓦时,1千瓦时俗称1度/时,实行“基本电价”;当居民家庭月用电量超过80千瓦时,超过部分实行“提高电价”(1)、小张家2017年2月份用电100千瓦时,上缴电费68元;3月份用电120千瓦时,上缴电费88元.求“基本电价”和“提高电价”分别为多少元/千瓦时?(2)、若4月份小张家预计用电130千瓦时,请预算小张家4月份应上缴的电费.19. 为宣传6月6日世界海洋日,某校九年级举行了主题为“珍惜海洋资源,保护海洋生物多样性”的知识竞赛活动.为了解全年级500名学生此次竞赛成绩(百分制)的情况,随机抽取了部分参赛学生的成绩,整理并绘制出如下不完整的统计表(表1)和统计图(如图).请根据图表信息解答以下问题:

 (1)、本次调查一共随机抽取了个参赛学生的成绩;(2)、表1中a=;(3)、所抽取的参赛学生的成绩的中位数落在的“组别”是;(4)、请你估计,该校九年级竞赛成绩达到80分以上(含80分)的学生约有人.20. 如图,一艘船由A港沿北偏东65°方向航行 km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向.
(1)、本次调查一共随机抽取了个参赛学生的成绩;(2)、表1中a=;(3)、所抽取的参赛学生的成绩的中位数落在的“组别”是;(4)、请你估计,该校九年级竞赛成绩达到80分以上(含80分)的学生约有人.20. 如图,一艘船由A港沿北偏东65°方向航行 km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向.
求:
(1)、∠C的度数;(2)、A,C两港之间的距离为多少km.21. 如图,正方形ABCD中,点E为AB上一动点(不与A、B重合).将△EBC沿CE翻折至△EFC,延长EF交边AD于点G. (1)、连结AF,若AF∥CE.证明:点E为AB的中点;(2)、证明:GF=GD;(3)、若AD=5,设EB=x,GD=y,求y与x的函数关系式.22. 如图,抛物线y= x2+bx+c与x轴交于点A(﹣1,0),B(4,0)与y轴交于点C,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线1,交抛物线与点Q.
(1)、连结AF,若AF∥CE.证明:点E为AB的中点;(2)、证明:GF=GD;(3)、若AD=5,设EB=x,GD=y,求y与x的函数关系式.22. 如图,抛物线y= x2+bx+c与x轴交于点A(﹣1,0),B(4,0)与y轴交于点C,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线1,交抛物线与点Q. (1)、求抛物线的解析式;(2)、当点P在线段OB上运动时,直线1交BD于点M,试探究m为何值时,四边形CQMD是平行四边形;(3)、在点P运动的过程中,坐标平面内是否存在点Q,使△BDQ是以BD为直角边的直角三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、当点P在线段OB上运动时,直线1交BD于点M,试探究m为何值时,四边形CQMD是平行四边形;(3)、在点P运动的过程中,坐标平面内是否存在点Q,使△BDQ是以BD为直角边的直角三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.