贵州省贵阳市白云区2019年数学中考一模试卷
试卷更新日期:2020-03-05 类型:中考模拟
一、单选题
-
1. 如图,在 中,点 为 边的中点,下列说法不正确的是( )
 A、 B、 C、 D、2. 甲、乙、丙、丁四位男同学在中考体育前进行 次立定跳远测试,平均成绩都是 米,方差分别是 ,则成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁3. 下列几何体是由4个相同的小正方体搭成的,其中左视图与俯视图相同的是( )A、
A、 B、 C、 D、2. 甲、乙、丙、丁四位男同学在中考体育前进行 次立定跳远测试,平均成绩都是 米,方差分别是 ,则成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁3. 下列几何体是由4个相同的小正方体搭成的,其中左视图与俯视图相同的是( )A、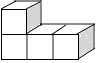 B、
B、 C、
C、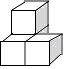 D、
D、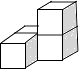 4. 方程 ax2+bx+c=0(a≠0)有实数根,那么成立的式子是( )A、b2-4ac>0 B、b2-4ac<0 C、b2-4ac≤0 D、b2-4ac≥05. 一根弹簧原长12 cm,它所挂的重量不超过10 kg,并且挂重1 kg就伸长1.5 cm,写出挂重后弹簧长度y(cm)与挂重x(kg)之间的函数关系式是( )A、y=1.5(x+12)(0≤x≤10) B、y=1.5x+12(0≤x≤10) C、y=1.5x+12(x≥0) D、y=1.5(x-12)(0≤x≤10)6. 甲、乙两人进行象棋比赛,比赛规则为3局2胜制.如果两人在每局比赛中获胜的机会均等,且比赛开始后,甲先胜了第1局,那么最后甲获胜的概率是()A、 B、 C、 D、7. 如图,四边形 是矩形,四边形 是正方形,点 在 轴的正半轴上,点 在 轴的正半轴上,点 在 上,点 在反比例函数 的图象上, ,则正方形 的面积为( )
4. 方程 ax2+bx+c=0(a≠0)有实数根,那么成立的式子是( )A、b2-4ac>0 B、b2-4ac<0 C、b2-4ac≤0 D、b2-4ac≥05. 一根弹簧原长12 cm,它所挂的重量不超过10 kg,并且挂重1 kg就伸长1.5 cm,写出挂重后弹簧长度y(cm)与挂重x(kg)之间的函数关系式是( )A、y=1.5(x+12)(0≤x≤10) B、y=1.5x+12(0≤x≤10) C、y=1.5x+12(x≥0) D、y=1.5(x-12)(0≤x≤10)6. 甲、乙两人进行象棋比赛,比赛规则为3局2胜制.如果两人在每局比赛中获胜的机会均等,且比赛开始后,甲先胜了第1局,那么最后甲获胜的概率是()A、 B、 C、 D、7. 如图,四边形 是矩形,四边形 是正方形,点 在 轴的正半轴上,点 在 轴的正半轴上,点 在 上,点 在反比例函数 的图象上, ,则正方形 的面积为( ) A、 B、 C、 D、8. 关于x的不等式组 只有 个整数解,则 的取值范围是( )A、 B、 C、 D、9. 如图,在正方形网格中,点 都在格点上,则 的值是( )
A、 B、 C、 D、8. 关于x的不等式组 只有 个整数解,则 的取值范围是( )A、 B、 C、 D、9. 如图,在正方形网格中,点 都在格点上,则 的值是( ) A、 B、 C、 D、10. 如图, 是 的直径, 是 的半径, 切 于点 , 与 的延长线相交于点 , . 已知 ,则 的长为( )
A、 B、 C、 D、10. 如图, 是 的直径, 是 的半径, 切 于点 , 与 的延长线相交于点 , . 已知 ,则 的长为( ) A、 B、 C、 D、11. 如图1,分别沿长方形纸片ABCD和正方形纸片EFGH的对角线AC,EG剪开,拼成如图2所示的▱ALMN,若中间空白部分四边形OPQR恰好是正方形,且▱ALMN的面积为50,则正方形EFGH的面积为( )
A、 B、 C、 D、11. 如图1,分别沿长方形纸片ABCD和正方形纸片EFGH的对角线AC,EG剪开,拼成如图2所示的▱ALMN,若中间空白部分四边形OPQR恰好是正方形,且▱ALMN的面积为50,则正方形EFGH的面积为( )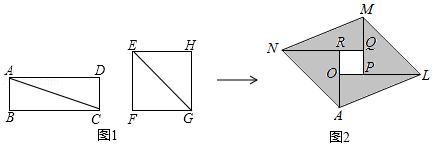 A、24 B、25 C、26 D、27
A、24 B、25 C、26 D、27二、填空题
-
12. 若 为任意实数,则 的最小值是.13. 把抛物线 向上平移 个单位,再向左平移 个单位,得到的抛物线的顶点坐标是.14. 如图,正六边形 的顶点 分别在正方形 的边 上,则 的度数是.如果 ,那么 的长为.
 15. 如果分式 的值为 ,那么 的值是.
15. 如果分式 的值为 ,那么 的值是.三、解答题
-
16. 如图,直线 与直线 在同一直角坐标中交于点 .
 (1)、直接写出方程组 的解是.(2)、请判断三条直线 ,是否经过同一个点,请说明理由.17. 某中学参加“创文明城市”书画比赛时,老师从全校 个班中随机抽取了 个班(用 表示),对抽取的作品的数量进行了分析统计,制作了两幅不完整的统计图.回答下列问题:
(1)、直接写出方程组 的解是.(2)、请判断三条直线 ,是否经过同一个点,请说明理由.17. 某中学参加“创文明城市”书画比赛时,老师从全校 个班中随机抽取了 个班(用 表示),对抽取的作品的数量进行了分析统计,制作了两幅不完整的统计图.回答下列问题: (1)、老师采用的调查方式是.(填“普查”或“抽样调查”);(2)、请补充完整条形统计图 , 并计算扇形统计图中 班作品数量所对应的圆心角度数度.(3)、请估计全校共征集作品的件数.18. 如图,小明的家在某住宅楼AB的最顶层(AB⊥BC),他家的后面有一建筑物CD(CD∥AB),他很想知道这座建筑物的高度,于是在自家阳台的A处测得建筑物CD的底部C的俯角是43°,顶部D的仰角是25°,他又测得两建筑物之间的距离BC是28米,请你帮助小明求出建筑物CD的高度(精确到1米).
(1)、老师采用的调查方式是.(填“普查”或“抽样调查”);(2)、请补充完整条形统计图 , 并计算扇形统计图中 班作品数量所对应的圆心角度数度.(3)、请估计全校共征集作品的件数.18. 如图,小明的家在某住宅楼AB的最顶层(AB⊥BC),他家的后面有一建筑物CD(CD∥AB),他很想知道这座建筑物的高度,于是在自家阳台的A处测得建筑物CD的底部C的俯角是43°,顶部D的仰角是25°,他又测得两建筑物之间的距离BC是28米,请你帮助小明求出建筑物CD的高度(精确到1米).(参考数据:sin25°≈0.42,cos25°≈0.91,tan25°≈0.47;sin43°≈0.68,cos43°≈0.73,tan43°≈0.93.)
 19. 端午节“赛龙舟,吃粽子”是中华民族的传统习俗.节日期间,小邱家包了三种不同馅的粽子,分别是:红枣粽子(记为A),豆沙粽子(记为B),肉粽子(记为C),这些粽子除了馅不同,其余均相同.粽子煮好后,小邱的妈妈给一个白盘中放入了两个红枣粽子,一个豆沙粽子和一个肉粽子;给一个花盘中放入了两个肉粽子,一个红枣粽子和一个豆沙粽子.
19. 端午节“赛龙舟,吃粽子”是中华民族的传统习俗.节日期间,小邱家包了三种不同馅的粽子,分别是:红枣粽子(记为A),豆沙粽子(记为B),肉粽子(记为C),这些粽子除了馅不同,其余均相同.粽子煮好后,小邱的妈妈给一个白盘中放入了两个红枣粽子,一个豆沙粽子和一个肉粽子;给一个花盘中放入了两个肉粽子,一个红枣粽子和一个豆沙粽子.根据以上情况,请你回答下列问题:
(1)、假设小邱从白盘中随机取一个粽子,恰好取到红枣粽子的概率是多少?(2)、若小邱先从白盘里的四个粽子中随机取一个粽子,再从花盘里的四个粽子中随机取一个粽子,请用列表法或画树状图的方法,求小邱取到的两个粽子中一个是红枣粽子、一个是豆沙粽子的概率.20. 如图,在 中, 是 边上的中线, 是 的中点,过点 作 的平行线交 的延长线于点 ,连接 . (1)、求证: ;(2)、若 ,试判断四边形 的形状,并证明你的结论.21. 兴发服装店老板用4500元购进一批某款T恤衫,由于深受顾客喜爱,很快售完,老板又用4950元购进第二批该款式T恤衫,所购数量与第一批相同,但每件进价比第一批多了9元.(1)、第一批该款式T恤衫每件进价是多少元?(2)、老板以每件120元的价格销售该款式T恤衫,当第二批T恤衫售出 时,出现了滞销,于是决定降价促销,若要使第二批的销售利润不低于650元,剩余的T恤衫每件售价至少要多少元?(利润=售价﹣进价)22. (理论学习)学习图形变换中的轴对称知识后,我们容易在直线 上找到点 ,使 的值最小,如图 所示,根据这一理论知识解决下列问题:
(1)、求证: ;(2)、若 ,试判断四边形 的形状,并证明你的结论.21. 兴发服装店老板用4500元购进一批某款T恤衫,由于深受顾客喜爱,很快售完,老板又用4950元购进第二批该款式T恤衫,所购数量与第一批相同,但每件进价比第一批多了9元.(1)、第一批该款式T恤衫每件进价是多少元?(2)、老板以每件120元的价格销售该款式T恤衫,当第二批T恤衫售出 时,出现了滞销,于是决定降价促销,若要使第二批的销售利润不低于650元,剩余的T恤衫每件售价至少要多少元?(利润=售价﹣进价)22. (理论学习)学习图形变换中的轴对称知识后,我们容易在直线 上找到点 ,使 的值最小,如图 所示,根据这一理论知识解决下列问题: (1)、(实践运用)如图 ,已知 的直径 为 ,弧 所对圆心角的度数为 ,点 是弧 的中点,请你在直径 上找一点 ,使 的值最小,并求 的最小值.
(1)、(实践运用)如图 ,已知 的直径 为 ,弧 所对圆心角的度数为 ,点 是弧 的中点,请你在直径 上找一点 ,使 的值最小,并求 的最小值. (2)、(拓展延伸)在图 中的四边形 的对角线 上找一点 ,使 .(尺规作图,保留作图痕迹,不必写出作法).
(2)、(拓展延伸)在图 中的四边形 的对角线 上找一点 ,使 .(尺规作图,保留作图痕迹,不必写出作法). 23. 如图,一次函数y=-x+5的图象与反比例函数y= (k≠0)在第一象限的图象交于A(1,n)和B两点.
23. 如图,一次函数y=-x+5的图象与反比例函数y= (k≠0)在第一象限的图象交于A(1,n)和B两点.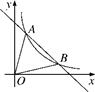 (1)、求反比例函数的解析式;(2)、在第一象限内,当一次函数y=-x+5的值大于反比例函数y= (k≠0)的值时,写出自变量x的取值范围.24. 在平面直角坐标系中,点 是原点,四边形 是矩形,点 ,点 .以点 为中心,顺时针旋转矩形 ,得到矩形 ,点 的对应点分别为 .
(1)、求反比例函数的解析式;(2)、在第一象限内,当一次函数y=-x+5的值大于反比例函数y= (k≠0)的值时,写出自变量x的取值范围.24. 在平面直角坐标系中,点 是原点,四边形 是矩形,点 ,点 .以点 为中心,顺时针旋转矩形 ,得到矩形 ,点 的对应点分别为 .
 (1)、如图①,当点 落在 边上时,求点 的坐标;(2)、如图②,当点 落在线段 上时, 与 交于点 .求点 的坐标;(3)、记 为矩形 对角线的交点, 为 的面积,求 的取值范围(直接写出结果即可).25. 如图,已知抛物线y= x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
(1)、如图①,当点 落在 边上时,求点 的坐标;(2)、如图②,当点 落在线段 上时, 与 交于点 .求点 的坐标;(3)、记 为矩形 对角线的交点, 为 的面积,求 的取值范围(直接写出结果即可).25. 如图,已知抛物线y= x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.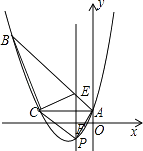 (1)、求抛物线的解析式;(2)、过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;(3)、当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;(3)、当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.