湖北省随州市2018-2019学年七年级下学期数学第一次月考试卷

试卷更新日期：2020-03-05 类型：月考试卷

进入出卷网下载

一、单选题

1. 下面四个图形中，∠1与∠2是对顶角的是（）

A、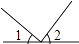 B、 C、 D、

查看试题解析
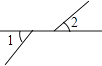2. 下列方程中不是二元一次方程的是（）

A、 $3 x - 5 y = 1$ B、 $\frac{x - 1}{4} = y$ C、 $xy = 7$ D、 $2 (m - n) = 9$

查看试题解析
3. 方程组： ${\begin{array}{l} 3 x + 7 y = 9 \\ 4 x - 7 y = 5 \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = - 2 \\ y = 1 \end{array}$ B、 ${\begin{array}{l} x = - 2 \\ y = \frac{3}{7} \end{array}$ C、 ${\begin{array}{l} x = 2 \\ y = - \frac{3}{7} \end{array}$ D、 ${\begin{array}{l} x = 2 \\ y = \frac{3}{7} \end{array}$

查看试题解析
4. 下列说法中正确的是（）

A、过一点有且只有一条直线平行于已知直线 B、两条直线被第三直线所截，同位角相等 C、两条直线有两种位置关系：平行、相交 D、同一平面内，垂直于同一条直线的两条直线平行

查看试题解析
5. 如图所示：若m∥n，∠1=105°，则∠2=（）

A、55° B、60° C、65° D、75°

查看试题解析
6. 如果二元一次方程ax+by+2=0有两个解 ${\begin{array}{l} x = 2 \\ y = 2 \end{array}$ 与 ${\begin{array}{l} x = 1 \\ y = - 1 \end{array}$ ，那么下列各组中仍是这个方程的解的是（）

A、 ${\begin{array}{l} x = 3 \\ y = 5 \end{array}$ B、 ${\begin{array}{l} x = 6 \\ y = 2 \end{array}$ C、 ${\begin{array}{l} x = 5 \\ y = 3 \end{array}$ D、 ${\begin{array}{l} x = 2 \\ y = 6 \end{array}$

查看试题解析
7. 如图，PO⊥OR，OQ⊥PR，则点O到PR所在直线的距离是线段（）的长.

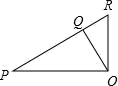A、OQ B、OR C、OP D、PQ

查看试题解析
8. 二元一次方程组 ${\begin{array}{l} 2 x + y = 5 k \\ 2 x - y = 7 k \end{array}$ 的解满足方程 $\frac{1}{3} x - 2 y = 5$ ，那么k的值为（）

A、 $\frac{3}{5}$ B、 $\frac{5}{3}$ C、 $- 5$ D、1

查看试题解析
9. 已知方程组 ${\begin{matrix} 5 x + y = 3 \\ a x + 5 y = 4 \end{matrix}$ 和 ${\begin{matrix} x - 2 y = 5 \\ 5 x + b y = 1 \end{matrix}$ 有相同的解，则a，b的值为（）

A、 ${\begin{matrix} a = 14 \\ b = 2 \end{matrix}$ B、 ${\begin{matrix} a = 4 \\ b = - 6 \end{matrix}$ C、 ${\begin{matrix} a = - 6 \\ b = 2 \end{matrix}$ D、 ${\begin{matrix} a = 1 \\ b = 2 \end{matrix}$

查看试题解析
10. 用“●”“■”“▲”分别表示三种不同的物体，如图所示，前两架天平保持平衡，若要使第三架天平也平衡，那么“？”处应放“■”的个数为（）

A、5个 B、4个 C、3个 D、2个

查看试题解析

二、填空题

11. 如图，直线a与b的关系是 .

查看试题解析
12. 如图，若AB∥CD，则下面结论中①∠1=∠2；②∠3=∠4；③∠1+∠3+∠D=180；④∠2+∠4+∠B=180°；正确的(填序号).

查看试题解析
13. 如图，AC⊥CB于C，CD⊥AB于D，下列关系中一定成立的是（填序号）
（ 1 ）AD＞CD；（2）CD＞BD；（3）BC＞BD；（4）AC＞BC.

查看试题解析
14. 四川5•12大地震后，灾区急需帐篷.某企业急灾区所急，准备捐助甲、乙两种型号的帐篷共2000顶，其中甲种帐篷每顶安置6人，乙种帐篷每顶安置4人，共安置9000人.设该企业捐助甲种帐篷x顶、乙种帐篷y顶，可列方程组为.

查看试题解析
15. 把图折叠成一个正方体，如果相对面的值相等，则一组x，y的值是.

查看试题解析
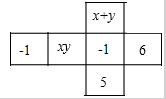16. 三个同学对问题“若方程组的 ${\begin{matrix} a_{1} x + b_{1} y = c_{1} \\ a_{2} x + b_{2} y = c_{2} \end{matrix}$ 解是 ${\begin{matrix} x = 3 \\ y = 4 \end{matrix}$ ，求方程组 ${\begin{matrix} 3 a_{1} x + 2 b_{1} y = 5 c_{1} \\ 3 a_{2} x + 2 b_{2} y = 5 c_{2} \end{matrix}$ 的解.”提出各自的想法.甲说：“这个题目好象条件不够，不能求解”；乙说：“它们的系数有一定的规律，可以试试”；丙说：“能不能把第二个方程组的两个方程的两边都除以5，通过换元替换的方法来解决”.参考他们的讨论，你认为这个题目的解应该是.

查看试题解析

三、解答题

17. 按要求作图（不写作法，但要保留作图痕迹）
已知点P、Q分别在∠AOB的边OA，OB上（如图所示）

①作直线PQ；

②过点P作OB的垂线；

③过点Q作OA的平行线.

查看试题解析
18. 如图，已知EF∥AD，∠1＝∠2，∠BAC＝70°，求∠AGD（请填空）

解：∵EF∥AD

∴∠2＝（）

又∵∠1＝∠2

∴∠1＝∠3（）

∴AB∥（）

∴∠BAC+＝180°（）

∵∠BAC＝70°（）

∴∠AGD＝（）

查看试题解析
19. 如图，已知：EB∥DC，∠A=∠ADE，你认为∠C和∠E相等吗？为什么？

查看试题解析
20. 李大叔今年五月份购买了一台彩电和一台洗衣机，根据“家电下乡”的补贴标准：农户每购买一件家电，国家将按每件家电售价的13%补贴给农户.因此，李大叔从乡政府领到了390元补贴款.若彩电的售价比洗衣机的售价高1000元，求彩电和洗衣机的售价各是多少元？

查看试题解析
21. 若关于x、y的二元一次方程租 ${\begin{array}{l} 3 x + 5 y = 2 \\ 2 x + 7 y = m - 18 \end{array}$ 的解x、y互为相反数，求m的值.

查看试题解析
22. 如图，在△ABC中，CD⊥AB，垂足为D. 点E在BC上，EF⊥AB，垂足为F，∠1=∠2.

(1)、试说明DG∥BC的理由；

(2)、如果∠B＝54°，且∠ACD=35°，求的∠3度数.

查看试题解析

23. 在“五一”期间，小明和他的父亲坐游船从甲地到乙地观光，在售票大厅他们看到了表(一)，在游船上，他又注意到了表(二).

表(一)

	里程(千米)	票价(元)
甲→乙	20	…
甲→丙	16	…
甲→丁	10	…
…	…	…

表(二)

	出发时间	到达时间
甲→乙	8：00	9：00
乙→甲	9：20	10：00
甲→乙	10：20	11：20
…	…	…

爸爸对小明说：“我来考考你，若船在静水中的速度保持不变，你能知道船在静水中的速度和水流速度吗？”小明很快得出了答案，你知道小明是如何算的吗？

查看试题解析

24. 问题情境：如图1，AB∥CD，∠PAB=130°，∠PCD=120°，求∠APC的度数.
小明的思路是：过P作PE∥AB，通过平行线性质来求∠APC.

(1)、按小明的思路，易求得∠APC的度数为度；

(2)、问题迁移：如图2，AB∥CD，点P在射线OM上运动，记∠PAB=α，∠PCD=β，当点P在B、D两点之间运动时，问∠APC与α、β之间有何数量关系？请说明理由；

(3)、在(2)的条件下，如果点P在B、D两点外侧运动时(点P与点O、B、D三点不重合)，请直接写出∠APC与α、β之间的数量关系.

查看试题解析