河南信阳市淮滨县王店乡2018-2019学年七年级下学期数学第一次月考试卷

试卷更新日期：2020-03-05 类型：月考试卷

进入出卷网下载

一、单选题

1. 如图，当光线从空气射入水中，光线的传播发生了改变，这就是折射现象.∠1的对顶角是（）

A、∠AOB B、∠BOC C、∠AOC D、都不是

查看试题解析
2. 如图所示，直线AB⊥CD于点O，直线EF经过点O，若∠1＝26°，则∠2的度数是（）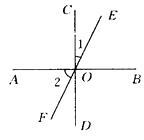

A、26° B、64° C、54° D、以上答案都不对

查看试题解析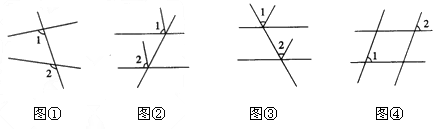
3. 已知图①～④，

在上述四个图中，∠1与∠2是同位角的有（）

A、①②③④ B、①②③ C、①③ D、①

查看试题解析
4. $\frac{9}{16}$ 的平方根是（）

A、 $\sqrt{\frac{3}{4}}$ B、± $\sqrt{\frac{3}{4}}$ C、 $\frac{3}{4}$ D、± $\frac{3}{4}$

查看试题解析
5. －8的立方根是（）

A、－2 B、－4 C、2 D、±2

查看试题解析
6. 在 $\sqrt{4} ， \frac{1}{3} ， 0 ， \frac{π}{7} ， \sqrt[3]{9} ， 4.21 ， 3.14$ 中，无理数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 若引 $\sqrt[3]{a} + \sqrt[3]{b} = 0$ ，则a与b的关系是（）

A、a=b=0 B、a=b C、a与b互为相反数 D、a= $\frac{1}{b}$

查看试题解析
8. 若 $m$ 、 $n$ 满足 ${(m - 1)}^{2} + \sqrt{n - 15} = 0$ ，则 $\sqrt{m + n}$ 的平方根是（）

A、 $\pm 4$ B、 $\pm 2$ C、 $4$ D、 $2$

查看试题解析
9. 把一副三角板放在同一水平桌面上，摆放成如图所示的形状，使两个直角顶点重合，两条斜边平行，则∠1的度数是（）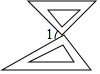

A、45° B、60° C、75° D、82.5°

查看试题解析
10. 如图，在直角三角形ABC中，∠BAC＝90°，AB＝3，AC＝4，将三角形ABC沿直线BC向右平移2.5个单位长度得到三角形DEF，连接AD，AE.有下列结论：①AC∥DF；②AD∥BE，AD＝BE；③∠ABE＝∠DEF；④ED⊥AC.其中正确的结论有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

11. 如图，直线AB，CD相交于点O，∠1－∠2＝50°，则∠2＝， ∠BOD＝.

查看试题解析
12. 数学课上，老师为同学们介绍了如图：A是线段BC外一点，连接AB，AC，过点A作线段BC的垂线AH.听完老师的介绍，小文说：在AB，AC，AH这三条线段中，AH是最短的线段.小文这样回答的依据是.

查看试题解析
13. 已知 $\sqrt{36} = x, \sqrt{y} = 3$ ，z是16的算术平方根，则2x＋y－5z的值为.

查看试题解析
14. 一个正数的平方根是 $x - 5$ 和 $x + 1$ ，则 $x$ 的值为 .

查看试题解析
15. 如图，将矩形ABCD折叠，折痕为EF，BC的对应边B'C′与CD交于点M，若∠B′MD=50°，则∠BEF的度数为.

查看试题解析

三、解答题

16. 计算：

(1)、 $\sqrt{3}$ ＋1＋3＋|1－ $\sqrt{3}$ |；

(2)、 $\sqrt{25} - \sqrt[3]{- 1} + \sqrt{144} + \sqrt[3]{- 64}$ .

查看试题解析
17. 如图，已知直线a∥b且被直线l所截，∠2＝85°，求∠1的度数.请在横线上补全求解的过程或依据.

查看试题解析
18. 画图并填空：

(1)、画出△ABC先向右平移6格，再向下平移2格得到的△A₁B₁C₁；

(2)、线段AA₁与BB₁的关系是；

(3)、△ABC的面积是平方单位.

查看试题解析
19. 如图，直线AB、CD相交于点O ， OM⊥AB.

(1)、若∠1＝∠2，判断ON与CD的位置关系，并说明理由.

(2)、若∠BOC＝4∠1，求∠MOD的度数.

查看试题解析
20. 如图，计划围一个面积为50 m²的长方形场地，一边靠旧墙(墙长为10 m)，另外三边用篱笆围成，并且它的长与宽之比为5∶2.讨论方案时，小英说：“我们不可能围成满足要求的长方形场地.”小军说：“面积和长宽比例是确定的，肯定可以围得出来.”请你判断谁的说法正确，为什么？

查看试题解析
21. 已知M＝ $a - b \sqrt{a + b + 3}$ 是a＋b＋3的算术平方根，N＝ $a - 2 b + 2 \sqrt{a + 6 b}$ 是a＋6b的算术平方根，求M·N的值.

查看试题解析
22. 阅读材料：
我们定义：如果一个数的平方等于－1，记作i²＝－1，那么这个i就叫做虚数单位.虚数与我们学过的实数结合在一起叫做复数，一个复数可以表示为a＋bi(a，b均为实数)的形式，其中a叫做它的实部，b叫做它的虚部.复数的加、减、乘的运算与我们学过的整式加、减、乘的运算类似.

例如：计算(5＋i)＋(3－4i)＝(5＋3)＋(i－4i)＝8－3i.

根据上述材料，解决下列问题：

(1)、填空：i³＝， i⁴＝；

(2)、计算：(6－5i)＋(－3＋7i)；

(3)、计算：3(2－6i)－4(5－i).

查看试题解析
23. 已知：如图，直线EF与AB，CD分别相交于点E，F.

(1)、如图1，若∠1＝120°，∠2＝60°，则AB和CD的位置关系为；

(2)、在(1)的情况下，若点P是平面内的一个动点，连接PE，PF，探索∠EPF，∠PEB，∠PFD三个角之间的关系：
①当点P在图2的位置时，可得∠EPF＝∠PEB＋∠PFD；

请阅读下面的解答过程，并填空(理由或数学式)：

解：如图2，过点P作MN∥AB，

则∠EPM＝∠PEB(两直线平行，内错角相等).

∵AB∥CD(已知)，MN∥AB(作图)，

∴MN∥CD(平行于同一条直线的两条直线互相平行).

∴∠MPF＝∠PFD.

∴∠EPM＋∠MPF＝∠PEB＋∠PFD(等式的性质)，

即∠EPF＝∠PEB＋∠PFD；

②当点P在图3的位置时，∠EPF，∠PEB，∠PFD三个角之间有何关系并证明；

③当点P在图4的位置时，请直接写出∠EPF，∠PEB，∠PFD三个角之间的关系.

查看试题解析