甘肃省定西市临洮县2019届九年级下学期数学第一次月考试卷

试卷更新日期：2020-03-05 类型：月考试卷

进入出卷网下载

一、单选题

1. $- 2019$ 的倒数是（）

A、 $- 2019$ B、 $- \frac{1}{2019}$ C、 $\frac{1}{2019}$ D、 $2019$

查看试题解析
2.
如图是一个由4个相同的长方体组成的立体图形，它的主视图是（　　）

A、 B、 C、 D、

查看试题解析
3. 下列计算正确的是（）

A、 ${(a^{2} b)}^{2} = a^{2} b^{2}$ B、 $a^{6} \div a^{2} = a^{3}$ C、 ${(3 x y^{2})}^{2} = 6 x^{2} y^{4}$ D、 ${(- m)}^{7} \div {(- m)}^{2} = - m^{5}$

查看试题解析
4. 下列说法正确的是（　　）

A、掷一枚质地均匀的正方体骰子，骰子停止转动后，5点朝上是必然事件 B、审查书稿中有哪些学科性错误适合用抽样调查法 C、甲乙两人在相同条件下各射击10次，他们的成绩的平均数相同，方差分别是S_甲²=0.4，S_乙²=0.6，则甲的射击成绩较稳定 D、掷两枚质地均匀的硬币，“两枚硬币都是正面朝上”这一事件发生的概率为 $\frac{1}{2}$

查看试题解析
5. 分式方程 $\frac{2 x}{x - 3} = 1$ 的解为（）

A、x=-2 B、x=-3 C、x=2 D、x=3

查看试题解析
6. 如图，l₁∥l₂ ， ∠1＝56°，则∠2的度数为（）

A、34° B、56° C、124° D、146°

查看试题解析
7. 若关于 $x$ 的一元二次方程 $(k - 1) x^{2} + 4 x + 1 = 0$ 有实数根，则 $k$ 的取值范围是（）

A、 $k ⩽ 5$ B、 $k ⩽ 5$ 且 $k \neq 1$ C、 $k < 5$ 且 $k \neq 1$ D、 $k < 5$

查看试题解析
8. 如图， $∠ A O B = 50 °$ ， $∠ O B C = 40 °$ ，则 $∠ O A C =$ （）

A、 $15 °$ B、 $25 °$ C、 $30 °$ D、 $40 °$

查看试题解析
9. 如图所示是小孔成像原理的示意图，根据图中所标注的尺寸，求出这支蜡烛在暗盒中所成像 $C D$ 的长（）

A、 $\frac{1}{6} c m$ B、 $\frac{1}{3} c m$ C、 $\frac{1}{2} c m$ D、 $1 c m$

查看试题解析
10. 二次函数 $y = {ax}^{2} + bx + c (a \neq 0)$ 的图像如图，下列结论：① $abc > 0$ ；② $4 ac - b^{2} < 0$ ；③ $3 b + 2 c < 0$ ；④ $a - b + c > 0$ .正确的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 太阳半径约是6.97万千米，科学记数法表示约是千米.

查看试题解析
12. 在函数 $y = \frac{1}{\sqrt{x + 1}}$ 中，自变量 $x$ 的取值范围是.

查看试题解析
13. 分解因式： $a^{3} - a b^{2}$ =.

查看试题解析
14. 某商品原价100元，连续两次涨价后，售价为144元.若平均每次增长率为 $x$ ，则 $x =$ .

查看试题解析
15. 一个扇形的弧长是20πcm，面积是240πcm² ，则这个扇形的圆心角是度．

查看试题解析
16. 将一张矩形纸片折叠成如图所示的图形，若AB=6cm，则AC=cm.

查看试题解析
17. 如图， $A B // C D$ ， $E$ ， $F$ 分别为 $A C$ ， $B D$ 的中点，若 $A B = 5$ ， $C D = 3$ ，则 $E F$ 的长是.

查看试题解析
18. 下列图形是用火柴棒摆成的“金鱼”，如果第1个图形需要8根火柴，则第2个图形需要14根火柴，第 $n$ 根图形需要根火柴.

查看试题解析

三、解答题

19. 计算： ${(- 1)}^{2018} + 2 \times \cos 60^{\circ} - {(- \frac{1}{2})}^{- 2} + {(\sqrt{3} - \sqrt{2})}^{0}$

查看试题解析
20. 先化简，再求值： $\frac{x^{2} +x}{x^{2} - 2 x + 1} \div (\frac{2}{x - 1} - \frac{1}{x})$ ，请你从﹣1≤x＜3的范围内选取一个适当的整数作为x的值．

查看试题解析
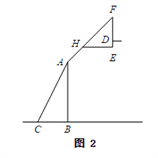
21. 如图1，2分别是某款篮球架的实物图与示意图，已知底座BC=0.60米，底座BC与支架AC所成的角∠ACB=75°，支架AF的长为2.50米米，篮板顶端F点到篮框D的距离FD=1.35米，篮板底部支架HF与支架AF所成的角∠FHE=60°，求篮框D到地面的距离（精确到0.01米）.
（参考数据：cos75°≈0.2588， sin75°≈0.9659，tan75°≈3.732， $\sqrt{3} \approx 1.732$ ， $\sqrt{2} \approx 1.414$ ）

查看试题解析
22. 某电视台的一档娱乐性节目中，在游戏PK环节，为了随机分选游戏双方的组员，主持人设计了以下游戏：用不透明的白布包住三根颜色长短相同的细绳AA₁、BB₁、CC₁ ，只露出它们的头和尾（如图所示），由甲、乙两位嘉宾分别从白布两端各选一根细绳，并拉出，若两人选中同一根细绳，则两人同队，否则互为反方队员.

(1)、若甲嘉宾从中任意选择一根细绳拉出，求他恰好抽出细绳AA₁的概率；

(2)、请用画树状图法或列表法，求甲、乙两位嘉宾能分为同队的概率.

查看试题解析
23. 如图，在平面直角坐标系中，一次函数 $y_{1} = k x + b (k \neq 0)$ 与反比例函数 $y_{2} = \frac{m}{x} (m \neq 0)$ 的图像交于点 $A (3 ， 1)$ 和点 $B$ ，且经过点 $C (0 ， - 2)$ .

(1)、求反比例函数和一次函数的表达式；

(2)、求当 $y_{1} > y_{2}$ 时自变量 $x$ 的取值范围.

查看试题解析
24. 如图，在 $Δ A B C$ 中，点 $F$ 是 $B C$ 的中点，点 $E$ 是线段 $A B$ 的延长线上的一动点，连接 $E F$ ，过点 $C$ 作 $A B$ 的平行线 $C D$ ，与线段 $E F$ 的延长线交于点 $D$ ，连接 $C E$ 、 $B D$ .

(1)、求证：四边形 $D B E C$ 是平行四边形.

(2)、若 $∠ A B C = 120 °$ ， $A B = B C = 4$ ，则在点 $E$ 的运动过程中：
①当 $B E =$ 时，四边形 $B E C D$ 是矩形；

②当 $B E =$ 时，四边形 $B E C D$ 是菱形.

查看试题解析
25. 如图，在 $RtΔABC$ 中， $∠ C = 90^{\circ}$ ， $AD$ 平分 $∠ BAC$ ，交 $BC$ 于点 $D$ ，点 $O$ 在 $AB$ 上， $⊙ O$ 经过 $A ， D$ 两点，交 $AB$ 于点 $E$ ，交 $AC$ 于点 $F$ .

(1)、求证： $BC$ 是 $⊙ O$ 的切线；

(2)、若 $⊙ O$ 的半径是 $2 cm$ ， $F$ 是弧 $AD$ 的中点，求阴影部分的面积（结果保留 $π$ 和根号）.

查看试题解析
26. 如图1，抛物线 $y = - x^{2} + b x + c$ 经过 $A (- 1 ， 0)$ ， $B (4 ， 0)$ 两点，与 $y$ 轴相交于点 $C$ ，连接 $B C$ .点 $P$ 为抛物线上一动点，过点 $P$ 作 $x$ 轴的垂线 $l$ ，交直线 $B C$ 于点 $G$ ，交 $x$ 轴于点 $E$ .

(1)、求抛物线的表达式；

(2)、当 $P$ 位于 $y$ 轴右边的抛物线上运动时，过点 $C$ 作 $C F ⊥$ 直线 $l$ ， $F$ 为垂足.当点 $P$ 运动到何处时，以 $P$ ， $C$ ， $F$ 为顶点的三角形与 $△ O B C$ 相似?并求出此时点 $P$ 的坐标；

(3)、如图2，当点 $P$ 在位于直线 $B C$ 上方的抛物线上运动时，连接 $P C$ ， $P B$ .请问 $△ P B C$ 的面积 $S$ 能否取得最大值?若能，请求出最大面积 $S$ ，并求出此时点 $P$ 的坐标；若不能，请说明理由.

查看试题解析