湖北省黄冈市2018-2019学年八年级下学期数学第一次月考试卷
试卷更新日期:2020-03-05 类型:月考试卷
一、单选题
-
1. 以下列各组数据中的三个数作为三角形的边长,其中能够成直角三角形的是( )A、3,5,7 B、5,7,9 C、3,2 , D、2,2 ,2. 下列判断正确的是( )A、 是最简二次根式 B、 与 不能合并 C、 一定是二次根式 D、二次根式的值必定是无理数3. 若 =﹣a ,则a的取值范围是( )A、﹣3≤a≤0 B、a≤0 C、a<0 D、a≥﹣34. 下列各式中,计算正确的是( )A、 B、 C、 D、5. 若 ≈1.414,则 的近似值是( )A、 B、0.707 C、1.414 D、2.8286. 2018年最强台风“山竹”9月16日上午11时登陆广东深圳,造成巨大的经济损失.如图台风“山竹”把一棵大树在离地面 5m 处折断,树顶落在离树根 12m 处,则大树在折断前高为( )
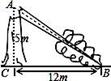 A、 18m B、13m C、17m D、12m7. 如图:矩形ABCD的对角线AC=10,BC=8,则图中五个小矩形的周长之和为( )
A、 18m B、13m C、17m D、12m7. 如图:矩形ABCD的对角线AC=10,BC=8,则图中五个小矩形的周长之和为( ) A、14 B、16 C、20 D、288. 有一长、宽、高分别是 5cm,4cm,3cm 的长方体木块,一只蚂蚁要从长方体的一个顶点 A处沿长方体的表面爬到长方体上和 A 相对的顶点 B 处,则需要爬行的最短路径长为( )
A、14 B、16 C、20 D、288. 有一长、宽、高分别是 5cm,4cm,3cm 的长方体木块,一只蚂蚁要从长方体的一个顶点 A处沿长方体的表面爬到长方体上和 A 相对的顶点 B 处,则需要爬行的最短路径长为( )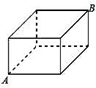 A、5 cm B、 cm C、4 cm D、3 cm
A、5 cm B、 cm C、4 cm D、3 cm二、填空题
-
9. 把 化为最简二次根式,结果是.10. 已知命题:若|a|=|b|,则 a2=b2 , 请写出该命题的逆命题.11. 若a,b都是实数,b= + ﹣2,则ab的值为.12. 计算( ﹣2)2018( +2)2019=.13. 若直角三角形的两边长为 a,b,且满足(a﹣3)2+|b﹣4|=0,则该直角三角形的斜边长为.14. 如图,所有阴影部分四边形都是正方形,所有三角形都是直角三角形,若正方形B、C、D的面积依次为4、3、9,则正方形A的面积为 .
 15. 如图,在△ABC中,∠ABC = 90°,AB = 2BC = 2,在AC上截取CD = CB.在AB上截取AP = AD,则AP = .
15. 如图,在△ABC中,∠ABC = 90°,AB = 2BC = 2,在AC上截取CD = CB.在AB上截取AP = AD,则AP = .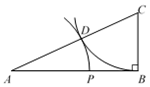 16. 如图,在一次测绘活动中,某同学站在点A的位置观测停放于B、C两处的小船,测得船B在点A北偏东75°方向900米处,船C在点A南偏东15°方向1200米处,则船B与船C之间的距离为米.
16. 如图,在一次测绘活动中,某同学站在点A的位置观测停放于B、C两处的小船,测得船B在点A北偏东75°方向900米处,船C在点A南偏东15°方向1200米处,则船B与船C之间的距离为米.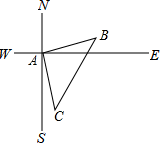
三、解答题
-
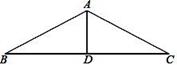
17. 计算:(1)、 ;(2)、 .18. 若 x、y 是实数,且 y= ,求 .19. 已知x= ﹣2,y= +2,求:(1)、x2y+xy2;(2)、 + 的值.20. 木工师傅做一个三角形屋梁架 ABC,如图所示,上弦 AB=AC=4m,跨度 BC 为 6m, 为牢固起见,还需做一根中柱 AD(AD 是△ABC 的中线)加以连接,现有一根长为 3m 的木料, 请你通过计算说明这根木料的长度是否适合加工成中柱 AD.
 21. 嘉淇准备完成题目:计算:(▓ , 发现系数“▓”印刷不清楚.(1)、他把“▓”猜成 3,请你计算:(3 .(2)、他妈妈说:“你猜错了,我看到该题标准答案的结果是 0.”请你通过计算说明原题中“▓”是几?22. 现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC中,∠ACB=90°,若AC=b,BC=a,请你利用这个图形解决下列问题:
21. 嘉淇准备完成题目:计算:(▓ , 发现系数“▓”印刷不清楚.(1)、他把“▓”猜成 3,请你计算:(3 .(2)、他妈妈说:“你猜错了,我看到该题标准答案的结果是 0.”请你通过计算说明原题中“▓”是几?22. 现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC中,∠ACB=90°,若AC=b,BC=a,请你利用这个图形解决下列问题: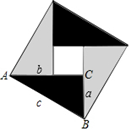 (1)、试说明a2+b2=c2;(2)、如果大正方形的面积是6,小正方形的面积是2,求(a+b)2的值.23. 如图,有一艘货船和一艘客船同时从港口A出发,客船每小时比货船多走5海里,客船与货船速度的比为4:3,货船沿东偏南10°方向航行,2小时后货船到达B处,客船到达C处,若此时两船相距50海里.
(1)、试说明a2+b2=c2;(2)、如果大正方形的面积是6,小正方形的面积是2,求(a+b)2的值.23. 如图,有一艘货船和一艘客船同时从港口A出发,客船每小时比货船多走5海里,客船与货船速度的比为4:3,货船沿东偏南10°方向航行,2小时后货船到达B处,客船到达C处,若此时两船相距50海里.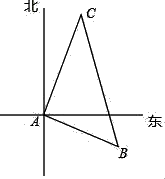 (1)、求两船的速度分别是多少?(2)、求客船航行的方向.24. 已知在等腰△ABC 中,AB=AC=10,BC=16.(1)、若将△ABC 的腰不变,底变为 12,甲同学说,这两个等腰三角形面积相等;乙同学说,腰不变,底变化,这两个三角形面积必不相等,请对甲、乙两种说法做出判断,并说明理由;(2)、已知△ABC 底边上高增加 x,腰长增加(x﹣2)时,底却保持不变,请确定 x 的值.25. (知识链接)斐波那契(约 1170﹣1250,意大利数学家)数列是按某种规律排列的一列数,他发现该数列中的每个正整数都可以用无理数的形式表示,如第 n(n 为正整数)个数 an 可表示为 .(1)、(知识运用)计算第一个数 a1 和第二个数 a2;(2)、(探究证明)证明连续三个数之间 an﹣1,an , an+1 存在以下关系:an+1﹣an=an﹣1(n≥2).(3)、(探究拓展)根据上面的关系,请写出斐波那契数列中的前 8 个数.
(1)、求两船的速度分别是多少?(2)、求客船航行的方向.24. 已知在等腰△ABC 中,AB=AC=10,BC=16.(1)、若将△ABC 的腰不变,底变为 12,甲同学说,这两个等腰三角形面积相等;乙同学说,腰不变,底变化,这两个三角形面积必不相等,请对甲、乙两种说法做出判断,并说明理由;(2)、已知△ABC 底边上高增加 x,腰长增加(x﹣2)时,底却保持不变,请确定 x 的值.25. (知识链接)斐波那契(约 1170﹣1250,意大利数学家)数列是按某种规律排列的一列数,他发现该数列中的每个正整数都可以用无理数的形式表示,如第 n(n 为正整数)个数 an 可表示为 .(1)、(知识运用)计算第一个数 a1 和第二个数 a2;(2)、(探究证明)证明连续三个数之间 an﹣1,an , an+1 存在以下关系:an+1﹣an=an﹣1(n≥2).(3)、(探究拓展)根据上面的关系,请写出斐波那契数列中的前 8 个数.