初中数学北师大版九年级下学期 第三章 3.3 垂径定理
试卷更新日期:2020-03-04 类型:同步测试
一、单选题
-
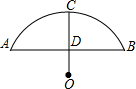
1. 如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=8,AE=1,则弦CD的长是( )
 A、 B、2 C、6 D、82. 一条排水管的截面如图所示,已知排水管的半径OA=1m,水面宽AB=1.2m,某天下雨后,水管水面上升了1.4m,则此时排水管水面宽为( )
A、 B、2 C、6 D、82. 一条排水管的截面如图所示,已知排水管的半径OA=1m,水面宽AB=1.2m,某天下雨后,水管水面上升了1.4m,则此时排水管水面宽为( )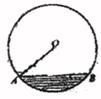 A、1.2m B、1.4m C、1.6m D、1.8m3. 嘉兴南湖不仅是党的诞生地,它优美的风光还吸引全国各地的旅客前来观赏.如图是南湖的一座三孔桥,某天测得最大桥拱的水面宽 为 ,桥顶 到水面 的距离为 ,则这座桥桥拱半径为
A、1.2m B、1.4m C、1.6m D、1.8m3. 嘉兴南湖不仅是党的诞生地,它优美的风光还吸引全国各地的旅客前来观赏.如图是南湖的一座三孔桥,某天测得最大桥拱的水面宽 为 ,桥顶 到水面 的距离为 ,则这座桥桥拱半径为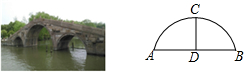 A、 B、 C、 D、4. 如图2,在平面直角坐标系中,点 的坐标为(1,4)、(5,4)、(1、 ),则 外接圆的圆心坐标是
A、 B、 C、 D、4. 如图2,在平面直角坐标系中,点 的坐标为(1,4)、(5,4)、(1、 ),则 外接圆的圆心坐标是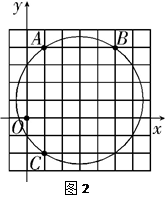 A、(2,3) B、(3,2) C、(1,3) D、(3,1)5. 如图,⊙O的直径CD垂直于弦AB于点E,且CE=2,DE=8,则AB的长为( )
A、(2,3) B、(3,2) C、(1,3) D、(3,1)5. 如图,⊙O的直径CD垂直于弦AB于点E,且CE=2,DE=8,则AB的长为( ) A、2 B、4 C、6 D、86. 如图,一条公路的转弯处是一段圆弧(AB),点O是这段弧所在圆的圆心,AB=40m,点C是AB的中点,且CD=10m,则这段弯路所在圆的半径为( )
A、2 B、4 C、6 D、86. 如图,一条公路的转弯处是一段圆弧(AB),点O是这段弧所在圆的圆心,AB=40m,点C是AB的中点,且CD=10m,则这段弯路所在圆的半径为( )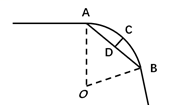 A、25m B、24m C、30m D、60m7. 如图,将半径为2的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长度为( )
A、25m B、24m C、30m D、60m7. 如图,将半径为2的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长度为( )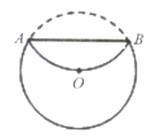 A、 B、2 C、2 D、(1+2 )
A、 B、2 C、2 D、(1+2 )二、填空题
-
8. 如图,在圆O中,弦AB=4,点C在AB上移动,连接OC,过点C做CD⊥OC交圆O于点D,则CD的最大值为。
 9. 如图,AB为圆O的弦,OC⊥AB,垂足为E,如果CE=2 ,AB=8 ,则圆O的半径为 .
9. 如图,AB为圆O的弦,OC⊥AB,垂足为E,如果CE=2 ,AB=8 ,则圆O的半径为 . 10. 如图,⊙O的半径OA等于5,半径OC与弦AB垂直,垂足为D,若OD=3,则弦AB的长为.
10. 如图,⊙O的半径OA等于5,半径OC与弦AB垂直,垂足为D,若OD=3,则弦AB的长为. 11. 如图,工程上常用钢珠来测量零件上小孔的宽度,假设钢珠的直径是12毫米,测得钢珠顶端离零件表面的距离为9毫米,则这个小孔的宽度AB是毫米。
11. 如图,工程上常用钢珠来测量零件上小孔的宽度,假设钢珠的直径是12毫米,测得钢珠顶端离零件表面的距离为9毫米,则这个小孔的宽度AB是毫米。 12. 已知⊙O中,弦AB=8cm,圆心到AB的距离为3cm,则此圆的半径为
12. 已知⊙O中,弦AB=8cm,圆心到AB的距离为3cm,则此圆的半径为
三、综合题